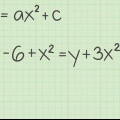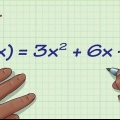Lembre-se que toda operação em um lado do sinal de igual também deve ser feita no outro lado. Exemplo: Para continuar com nosso exemplo, primeiro adicionamos 2 em ambos os lados da equação. Isso nos dá y + 2 = 5x. Então dividimos ambos os lados da equação por 5, deixando (y + 2)/5 = x. Finalmente, para torná-lo mais legível, reescrevemos a equação com o "X" Para a esquerda: x = (y + 2)/5. 
Exemplo: Depois de trocar x e y, obtemos y = (x + 2)/5 
Porque X é igual a 1/x, você também pode escrever f(x) como "1/f(x)," outra notação para o inverso de f(x). 
Exemplo: vamos inserir 4 como o valor de X em nossa comparação original. Isso nos dá f(x) = 5(4) - 2, ou f(x) = 18. Em seguida, vamos inserir este resultado no inverso. Então substituímos 18 na função inversa como o valor de X. Ao fazer isso, obtemos y = (18 + 2)/5 como resultado e isso é igual a y = 4. Então 4 é o valor x com o qual começamos e com isso sabemos que encontramos a função inversa correta.
Encontrando a inversa de uma função
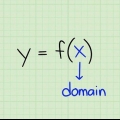
Uma função em matemática (geralmente notada como f(x)) pode ser pensada como um tipo de fórmula ou programa onde você insere um valor "X" encaixa, que então retorna um determinado valor para y. O inverso de uma função f(x) (notada como f(x)) é essencialmente o inverso: insira um y-valor e você recebe o mais cedo X-valor de volta. Encontrar a inversa de uma função pode parecer complicado, mas para equações simples, tudo o que você precisa é de algum conhecimento das operações básicas da álgebra. Leia as seguintes instruções passo a passo e dê uma boa olhada no exemplo.
Degraus

1. Escreva sua função, trocando f(x) por y se necessário. Sua fórmula pertence y ter de um lado o sinal de igual e do outro o X-termos. Se você tiver uma equação já escrita em y e X termos (como por exemplo 2 + y = 3x), então você só precisa y resolver isolando-o.
- Exemplo: Temos uma função f(x) = 5x - 2, e a reescrevemos como y = 5x - 2, simplesmente por "f(x)" ser substituído por y.
- Nota: f(x) é a notação de função padrão, mas se você estiver lidando com várias funções, cada função receberá uma letra inicial diferente para facilitar a distinção. Por exemplo, g(x) e h(x) são letras comumente usadas para funções.

2. solto X sobre. Em outras palavras, faça as edições necessárias para X isolar de um lado do sinal de igual. Para fazer isso, use as operações básicas da álgebra: se X tem um coeficiente (um número para a variável), divida ambos os lados da equação por este número para cancelá-lo; existe uma constante dentro do "X"-termo, então resolva adicionando ou subtraindo ambos os lados do sinal de igual, e assim por diante.

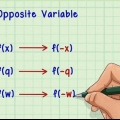
3. Troque as variáveis. Troca X de y e vice versa. A equação resultante é a inversa da função original. Em outras palavras, se tivermos um valor para X preencha nossa equação original, então podemos preencher a resposta no inverso (novamente para "X") que retorna o valor original!

4. substituir y por meio de "f(x)". As funções inversas são geralmente notadas como f(x) = (x termos) . Lembre-se que neste caso o expoente -1 não significa que temos que realizar uma operação exponencial na função. É apenas uma maneira de indicar que esta função é a inversa da original.

5. Verifique seu trabalho. Tente preencher uma constante na função original para X. Se você encontrou o inverso correto, então você encontraria o valor original de "X" deve vê-lo novamente, se você inserir o resultado disso no inverso.
Pontas
- Você pode usar ambas as notações f(x) = y e f^(-1)(x) = y sem problemas se você fizer operações matemáticas nas funções. Mas é melhor manter a função original e a função inversa separadas, então tente mantê-la em notação comum. No caso da função inversa, a notação f^(-1)(x).
- Observe que a inversa de uma função é geralmente, mas nem sempre, uma função em si.
Artigos sobre o tópico "Encontrando a inversa de uma função"
Оцените, пожалуйста статью
Similar
Popular