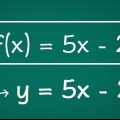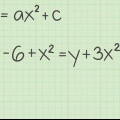Um polinômio sem raízes ou frações com variáveis no denominador. O domínio deste tipo de função consiste no conjunto de todos os números reais. Uma função com uma fração com uma variável no denominador. Para encontrar o domínio desse tipo de função, defina o denominador da fração igual a zero e ignore o valor de x encontrado após resolver a equação. Uma função com uma variável dentro de um radical. Para encontrar o domínio desse tipo de função, defina os termos dentro do radical maior que 0 e resolva a equação para descobrir quais valores para x estão corretos dentro dessa função. Uma função com logaritmo natural (ln). Faça os termos entre parênteses >0 e resolver. Um gráfico. Deduza do gráfico quais valores estão corretos para x. Um relacionamento. Esta é uma lista de coordenadas x e y. Seu domínio é simplesmente uma lista de coordenadas x. 
A estrutura de um domínio é um colchete/colchete aberto, seguido pelos 2 pontos finais do domínio separados por uma vírgula e seguido por um colchete/colchete de fechamento. Por exemplo: [-1,5). Isso significa que o domínio vai de -1 a 5. Use colchetes como [ e ] para indicar se um número está dentro de um determinado domínio. Então, no exemplo, [-1.5), -1 está dentro do domínio. Use parênteses como ( e ) para indicar que um número está fora de um determinado domínio. Então, no exemplo, [-1.5), o 5 está fora do domínio. O domínio para em qualquer ponto antes do 5, por exemplo 4.999… Use “U” (significando "União") para conectar partes do domínio que estão separadas umas das outras.` Por exemplo: [-1,5) U (5,10]. Isso significa que o domínio vai de -1 a 10, mas há uma lacuna no domínio em 5. Por exemplo, isso pode ser devido a uma função com “x - 5” no denominador. você pode fazer tanto "VOCÊS"-use símbolos conforme necessário, se o domínio tiver várias quebras. Use o símbolo do infinito (nas direções positiva e negativa) para indicar que nessa direção o domínio é infinito. No infinito, use sempre ( ) e não [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x ≠ (2, - 2) 
x = todos os números reais, exceto 2 e -2 

x-7 0 
x 7 
D = [7,∞) 
Agora verifique a área abaixo de -2 (por exemplo,. -3), se isso dá um resultado maior que zero. Está certo. (-3) - 4 = 5 Agora verifique a área entre -2 e 2. Por exemplo, tome 0. 0 - 4 = -4, então você sabe que os números entre -2 e 2 não funcionam. Agora tente um número acima de 2, como +3. 3 - 4 = 5, então os números acima de 2 funcionam. Anote o domínio quando terminar. Veja como escrever isso: D = (-∞, -2) U (2, ∞) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 X > 8 
D = (8,∞) 

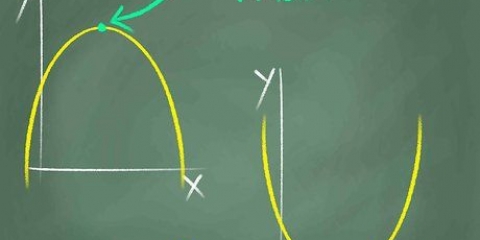
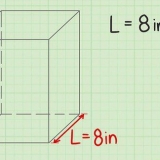
Uma linha. Se você vir uma linha no gráfico indo para o infinito, eventualmente todo valor x estará contido na parábola, então o domínio é igual a todos os números reais. Uma parábola comum. Se você vir uma parábola apontando para cima ou para baixo, então o domínio consiste em todos os números reais, porque todos os números no eixo x estão contidos na parábola. Uma parábola horizontal. Se você está lidando com uma parábola com o vértice em (4,0) que se estende infinitamente para a direita, então seu domínio é igual a D = [4,∞) 




Encontrando o domínio de uma função
Contente
- Degraus
- Método 1 de 6: Aprendendo o básico
- Método 2 de 6: Encontrando o domínio de uma função que contém uma fração
- Método 3 de 6: Encontrando o domínio de uma função com raiz quadrada
- Método 4 de 6: Encontrando o domínio de uma função usando o logaritmo natural
- Método 5 de 6: Encontrando o domínio de uma função usando um gráfico
- Método 6 de 6: Determinando o domínio de uma função usando uma coleção/relacionamento
O domínio de uma função é uma coleção de números que cabem dentro dessa função. Em outras palavras, é uma coleção de valores x associados a uma determinada equação. O conjunto de valores y é chamado faixa de função. Se você gostaria de saber como encontrar o domínio de uma função em diferentes situações, siga estes passos.
Degraus
Método 1 de 6: Aprendendo o básico

1. Aprenda a definição de um domínio. Um domínio de uma função é definido como o conjunto de todos os números reais que podem servir como entradas para essa função. Em outras palavras, um domínio é o conjunto completo de valores x inseridos em uma função, o que resulta em um conjunto de valores y.

2. Aprenda a encontrar o domínio de diferentes funções. O tipo de recurso determinará o melhor método para encontrar um domínio. Aqui está o básico que você precisará para as seguintes funções:

3. Compreender a notação de um domínio. A notação correta de um domínio é fácil de aprender, mas é importante que você faça isso corretamente para não perder pontos em testes e exames. Aqui estão algumas coisas que você precisa saber para escrever corretamente o domínio de uma função:
Método 2 de 6: Encontrando o domínio de uma função que contém uma fração

1. Escreva a tarefa. Suponha que você tenha o seguinte problema:
- f(x) = 2x/(x - 4)

2. Para frações com uma variável no denominador, você define essa variável igual a zero em uma equação. Se você quiser encontrar o domínio de uma função com uma fração, exclua todos os valores de x que tornam o denominador igual a zero, pois você nunca pode dividir por zero. Então escreva o denominador como uma equação e iguale a 0. Aqui está como fazê-lo:

3. Anote o domínio. Aqui está como fazê-lo:
Método 3 de 6: Encontrando o domínio de uma função com raiz quadrada

1. Escreva a tarefa. Suponha que você tenha o seguinte problema: Y = (x-7)

2. Certifique-se de que os termos dentro da raiz quadrada podem ser maiores ou iguais a 0. Você não pode tirar a raiz quadrada de um número negativo, mas pode tirar a raiz quadrada de zero. Observe que isso se aplica não apenas às raízes quadradas, mas a todas as raízes pares. Não se aplica a números radicais ímpares, porque não é um problema se houver um número negativo sob o sinal de radical. Aqui está um exemplo:

3. Isolar a variável. Agora para separar x do lado esquerdo da equação, some 7 em ambos os lados do sinal de igual, para que após esta operação fique assim:

4. Escreva o domínio corretamente. Esta é a notação correta:

5. Encontre o domínio de uma função com raiz quadrada se várias soluções são possíveis. Suponha que você tenha a seguinte função: y = 1/√( ̅x -4). Se você pegar o denominador fora dos parênteses e torná-lo igual a zero, você obtém x ≠ (2, - 2). Veja como proceder:
Método 4 de 6: Encontrando o domínio de uma função usando o logaritmo natural

1. Escreva a tarefa. Suponha que você tenha isso:
- f(x) = ln(x-8)

2. Torne os termos dentro dos parênteses maiores que zero. O logaritmo natural deve ser positivo, então faça os termos dentro dos parênteses maiores que zero. Aqui está um exemplo:

3. Resolver. Separe a variável x adicionando 8 a ambos os lados da equação. Veja como:

4. Anote o domínio. Mostre que o domínio desta equação é igual a todos os números maiores que 8 ao infinito. Veja como:
Método 5 de 6: Encontrando o domínio de uma função usando um gráfico

1. Veja o gráfico.

2. Investigue quais valores x pertencem ao gráfico. Isso é mais fácil falar do que fazer, então aqui estão algumas dicas:

3. Determinar o domínio. Determine o domínio com base no tipo de gráfico que você tem. Se você não tem certeza, mas conhece a equação da reta, insira as coordenadas x na função para verificar.
Método 6 de 6: Determinando o domínio de uma função usando uma coleção/relacionamento

1. Anote o relacionamento. Uma relação é simplesmente uma série de coordenadas x e y. Suponha que você tenha as seguintes coordenadas: {(1, 3), (2, 4), (5, 7)}

2. Anote as coordenadas x. São eles: 1, 2, 5.

3. Determinar o domínio. D = {1, 2, 5}

4. Certifique-se de que esta relação é uma função. Uma relação é uma função se cada vez que você digita uma coordenada x numérica você obtém a mesma coordenada y como resposta. Então, se você colocar um 3 na frente do x, você obtém 6 como o valor de y, e assim por diante. A próxima relação é não uma função porque você obtém dois valores y diferentes para cada valor de "X": {(1, 4),(3, 5),(1, 5)}.
Artigos sobre o tópico "Encontrando o domínio de uma função"
Оцените, пожалуйста статью
Similar
Popular