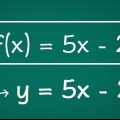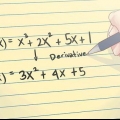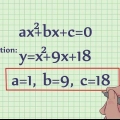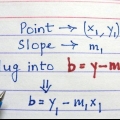Veja o exemplo de comparação  , onde os termos y podem ser movidos para a esquerda subtraindo um y de ambos os lados. Os outros termos podem ser movidos para o lado direito adicionando 6 em ambos os lados e
, onde os termos y podem ser movidos para a esquerda subtraindo um y de ambos os lados. Os outros termos podem ser movidos para o lado direito adicionando 6 em ambos os lados e  para retirar de ambos os lados. A equação resultante é
para retirar de ambos os lados. A equação resultante é  .
. 
Veja a comparação de exemplo  . Não há limitação nos valores permitidos de x para esta equação. No entanto, você deve perceber que esta é a equação de uma parábola, com x = 0 como seu centro, e uma parábola não é uma função porque não é uma comparação um-para-um dos valores de x e y. Para limitar esta equação e torná-la uma função, para a qual podemos encontrar uma inversa, precisamos definir o domínio como x≥0.
. Não há limitação nos valores permitidos de x para esta equação. No entanto, você deve perceber que esta é a equação de uma parábola, com x = 0 como seu centro, e uma parábola não é uma função porque não é uma comparação um-para-um dos valores de x e y. Para limitar esta equação e torná-la uma função, para a qual podemos encontrar uma inversa, precisamos definir o domínio como x≥0. O alcance é limitado da mesma forma. Observe que o primeiro termo,  , será sempre positivo ou 0, para qualquer valor de x. Então, se a equação somar +2, o intervalo será qualquer valor y≥2.
, será sempre positivo ou 0, para qualquer valor de x. Então, se a equação somar +2, o intervalo será qualquer valor y≥2. Definir o domínio e o escopo neste estágio inicial é necessário. Você usará essas definições mais tarde ao definir o domínio e o escopo da função inversa. Na verdade, o domínio da função original torna-se o domínio da função inversa, e o domínio da função original torna-se o domínio da função inversa. 
Trabalhando com a comparação de exemplo  , este passo de inversão resultará na nova equação de
, este passo de inversão resultará na nova equação de  .
. Um formato alternativo é substituir os termos y por x, mas substituir os termos x por  ou
ou  para indicar a função inversa.
para indicar a função inversa. 
 (premissa original)
(premissa original) (subtrair 2 de ambos os lados)
(subtrair 2 de ambos os lados) (dividir ambos os lados por 2)
(dividir ambos os lados por 2)± (raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada resulta em respostas possíveis positivas e negativas)
(raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada resulta em respostas possíveis positivas e negativas) 
Veja a solução da equação de exemplo ± . Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser
. Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser  seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥2. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥0, se você pegar a solução positiva da raiz quadrada, ou y≤0, se você pegar a solução negativa de a raiz quadrada. Observe que para encontrar a função inversa, você originalmente definiu o domínio como x≥0. Portanto, a solução correta para a função inversa é a opção positiva.
seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥2. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥0, se você pegar a solução positiva da raiz quadrada, ou y≤0, se você pegar a solução negativa de a raiz quadrada. Observe que para encontrar a função inversa, você originalmente definiu o domínio como x≥0. Portanto, a solução correta para a função inversa é a opção positiva. Compare o domínio e imagem da inversa com o domínio e imagem do original. Lembre-se que para a função original,  , o domínio foi definido como todos os valores de x≥0, e o intervalo foi definido como todos os valores de y≥2. Para a função inversa, agora esses valores trocam, e o domínio são todos os valores de x≥2, e o intervalo são todos os valores de y≥0.
, o domínio foi definido como todos os valores de x≥0, e o intervalo foi definido como todos os valores de y≥2. Para a função inversa, agora esses valores trocam, e o domínio são todos os valores de x≥2, e o intervalo são todos os valores de y≥0. 
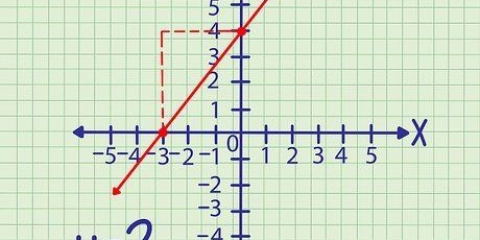
Como exemplo, escolha o valor x=1 para a equação original  . Isso dá o resultado y = 4.
. Isso dá o resultado y = 4. Então você coloca o valor 4 na função inversa  . Isso realmente dá o resultado y = 1. Você pode concluir que sua função inversa está correta.
. Isso realmente dá o resultado y = 1. Você pode concluir que sua função inversa está correta. 

Observe que esta forma padrão consiste em um termo quadrático perfeito,  , que é então modificado pelos outros dois elementos a e k. Para chegar a esta forma quadrática perfeita, você terá que criar certas condições em sua equação quadrática.
, que é então modificado pelos outros dois elementos a e k. Para chegar a esta forma quadrática perfeita, você terá que criar certas condições em sua equação quadrática. 
Para completar o quadrado, trabalhe no sentido inverso. Você começa com  e um segundo termo x. Do coeficiente desse termo, que você pode definir como `2b`, você deve obter
e um segundo termo x. Do coeficiente desse termo, que você pode definir como `2b`, você deve obter  ver para encontrar. Isso requer uma combinação de dividir por dois e, em seguida, elevar ao quadrado esse resultado.
ver para encontrar. Isso requer uma combinação de dividir por dois e, em seguida, elevar ao quadrado esse resultado. 
Tomemos, por exemplo, a função quadrática  . Você pode simplificar isso dividindo todos os termos por 2 para obter a função resultante
. Você pode simplificar isso dividindo todos os termos por 2 para obter a função resultante  para obter. O coeficiente 2 fica fora dos colchetes e fará parte da sua solução final.
para obter. O coeficiente 2 fica fora dos colchetes e fará parte da sua solução final. Se todos os termos não são múltiplos de a, você obtém coeficientes fracionários. Por exemplo: a função  será simplificado para
será simplificado para  . Calcule as frações com cuidado.
. Calcule as frações com cuidado. 
Por exemplo, se os dois primeiros termos da sua função quadrática  você encontra o terceiro termo necessário dividindo 3 por 2 (ou 3/2), e então elevando ao quadrado, para obter 9/4. O quadrático
você encontra o terceiro termo necessário dividindo 3 por 2 (ou 3/2), e então elevando ao quadrado, para obter 9/4. O quadrático  é um quadrado perfeito.
é um quadrado perfeito. Outro exemplo: suponha que os dois primeiros termos  são. Metade do termo médio é -2, e então você eleva ao quadrado para obter 4. O quadrado perfeito resultante é
são. Metade do termo médio é -2, e então você eleva ao quadrado para obter 4. O quadrado perfeito resultante é  .
. 
Suponha que você tenha a função  . Como mencionado acima, você usa os dois primeiros termos para completar o quadrado. Usando o termo médio de -4x, você gera um terceiro termo +4. Adicione 4 e subtraia 4 da equação, na forma
. Como mencionado acima, você usa os dois primeiros termos para completar o quadrado. Usando o termo médio de -4x, você gera um terceiro termo +4. Adicione 4 e subtraia 4 da equação, na forma  . Os parênteses são colocados apenas para definir a equação quadrática que você está fazendo. Observe o +4 dentro dos colchetes e o -4 do lado de fora. Simplifique os números para o resultado
. Os parênteses são colocados apenas para definir a equação quadrática que você está fazendo. Observe o +4 dentro dos colchetes e o -4 do lado de fora. Simplifique os números para o resultado  .
. 
Observe que para esta função a=1, h=2 e k=5. O valor de escrever a equação nesta forma é que a, por ser positivo, diz que a parábola está apontando para cima. Os valores (h, k) indicam o vértice na parte inferior da parábola, se você quiser grafá-lo. 
Continue trabalhando com a função de visualização  . Como este está no formato padrão, você pode determinar o vértice como x=2, y=5. Então para evitar a simetria, você só trabalha com o lado direito do gráfico, e define o domínio se todos os valores x≥2. Inserir o valor x=2 na função retorna y=5. Você pode ver que os valores de y aumentarão à medida que x aumenta. Portanto, o alcance desta equação é y≥5.
. Como este está no formato padrão, você pode determinar o vértice como x=2, y=5. Então para evitar a simetria, você só trabalha com o lado direito do gráfico, e define o domínio se todos os valores x≥2. Inserir o valor x=2 na função retorna y=5. Você pode ver que os valores de y aumentarão à medida que x aumenta. Portanto, o alcance desta equação é y≥5. 
Continue trabalhando com a função  . Insira x no lugar de f(x), e insira y (ou f(x), se preferir) no lugar de x. Isso dá como uma nova função
. Insira x no lugar de f(x), e insira y (ou f(x), se preferir) no lugar de x. Isso dá como uma nova função  .
. 
 (ponto de partida original)
(ponto de partida original) (subtrair 5 de ambos os lados)
(subtrair 5 de ambos os lados)± (raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada produz respostas possíveis positivas e negativas)
(raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada produz respostas possíveis positivas e negativas) ± (adicione 2 em ambos os lados)
(adicione 2 em ambos os lados) 
Veja a solução da equação de exemplo ± . Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser
. Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser  seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥5. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥2 (se você pegar a solução positiva da raiz quadrada), ou y≤2 (se você escolher a solução negativa da raiz quadrada). Lembre-se que você originalmente definiu o domínio como x≥2, para encontrar a função inversa. Portanto, a solução correta para a função inversa é a opção positiva.
seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥5. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥2 (se você pegar a solução positiva da raiz quadrada), ou y≤2 (se você escolher a solução negativa da raiz quadrada). Lembre-se que você originalmente definiu o domínio como x≥2, para encontrar a função inversa. Portanto, a solução correta para a função inversa é a opção positiva. Compare o domínio e imagem da inversa com o domínio e imagem do original. Lembre-se que para a função original, o domínio foi definido como todos os valores de x≥2, e o intervalo foi definido como todos os valores de y≥5. Para esta função inversa, esses valores se trocam, e o domínio agora é todos os valores de x≥5, e o intervalo é todos os valores de y≥2. 
Como exemplo, escolha o valor x=3 para incluir na equação original  processar. Isso dá o resultado y = 6.
processar. Isso dá o resultado y = 6. Então você processa y = 6 na função inversa  . Isso retorna y=3, que é o número com o qual você começou. Você pode concluir que sua função inversa está correta.
. Isso retorna y=3, que é o número com o qual você começou. Você pode concluir que sua função inversa está correta. 

Para esta seção deste artigo, você usará a equação de amostra  .
. 

Com base na equação de trabalho  , isso dá o resultado
, isso dá o resultado  .
. 
Para a equação de exemplo, para obter o lado esquerdo igual a zero, você precisa subtrair x de ambos os lados da equação. Isso dá o resultado  .
. 
Sair  . Então, x = 1
. Então, x = 1 Sair  . Então, b = 2
. Então, b = 2 Sair  . Então, c=(-3-x)
. Então, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Este último passo é possível porque você trocou f(x) pela variável x em um estágio anterior). 




Assumindo a função original  , escolha seu x=-2. Isso retorna y=-3. Agora substitua o valor de x=-3 na função inversa,
, escolha seu x=-2. Isso retorna y=-3. Agora substitua o valor de x=-3 na função inversa,  . Isso retorna -2, que é de fato o valor com o qual você começou. Então sua definição da função inversa está correta.
. Isso retorna -2, que é de fato o valor com o qual você começou. Então sua definição da função inversa está correta.
Encontrando a inversa de uma equação quadrática
Contente
As funções inversas podem ser muito úteis na resolução de muitos problemas matemáticos. Ser capaz de pegar uma função e encontrar sua função inversa é uma ferramenta poderosa. No entanto, com equações quadráticas, isso pode ser um processo bastante complicado. Primeiro você precisa definir cuidadosamente a equação, determinando um domínio e um intervalo apropriados. Você então tem uma escolha de três métodos para calcular a função inversa. A escolha do método é principalmente uma questão de preferência pessoal.
Degraus
Método 1 de 3: Encontrando a inversa de uma função simples

1. Encontre uma função na forma de y = uma X 2 + c  . Se você tiver o tipo de função `certo` para começar, poderá encontrar o inverso com alguma álgebra simples. Esta forma é uma espécie de variação
. Se você tiver o tipo de função `certo` para começar, poderá encontrar o inverso com alguma álgebra simples. Esta forma é uma espécie de variação  . Se você comparar isso com uma função quadrática padrão,
. Se você comparar isso com uma função quadrática padrão,  , veja que o meio termo
, veja que o meio termo  está desaparecido. Outra maneira de dizer isso é que o valor de b é zero. Se sua função tem esta forma, encontrar a inversa é bem fácil.
está desaparecido. Outra maneira de dizer isso é que o valor de b é zero. Se sua função tem esta forma, encontrar a inversa é bem fácil.
 . Se você tiver o tipo de função `certo` para começar, poderá encontrar o inverso com alguma álgebra simples. Esta forma é uma espécie de variação
. Se você tiver o tipo de função `certo` para começar, poderá encontrar o inverso com alguma álgebra simples. Esta forma é uma espécie de variação  . Se você comparar isso com uma função quadrática padrão,
. Se você comparar isso com uma função quadrática padrão,  , veja que o meio termo
, veja que o meio termo  está desaparecido. Outra maneira de dizer isso é que o valor de b é zero. Se sua função tem esta forma, encontrar a inversa é bem fácil.
está desaparecido. Outra maneira de dizer isso é que o valor de b é zero. Se sua função tem esta forma, encontrar a inversa é bem fácil. - Sua função inicial não precisa ser exatamente igual
. Contanto que você possa olhar para ele e ver que a função consiste apenas em
termos e números constantes, você poderá usar este método.
- Suponha que você comece com a equação
. Um rápido exame desta equação revela que não há termos de
estar na primeira potência. Esta equação é candidata a este método para encontrar uma função inversa.

2. Simplifique combinando termos semelhantes. A equação inicial pode ter vários termos em uma combinação de adição e subtração. Seu primeiro passo é combinar termos semelhantes para simplificar a equação e reescrevê-la no formato padrão  .
.
 .
. , onde os termos y podem ser movidos para a esquerda subtraindo um y de ambos os lados. Os outros termos podem ser movidos para o lado direito adicionando 6 em ambos os lados e
, onde os termos y podem ser movidos para a esquerda subtraindo um y de ambos os lados. Os outros termos podem ser movidos para o lado direito adicionando 6 em ambos os lados e  para retirar de ambos os lados. A equação resultante é
para retirar de ambos os lados. A equação resultante é  .
.
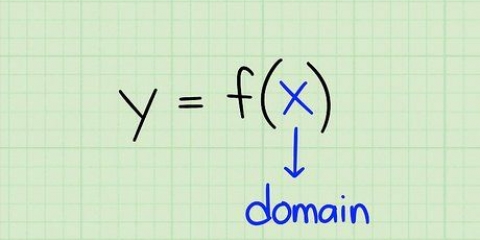
3. Determine o domínio e a imagem da função simplificada. Lembre-se que o domínio de uma função consiste nos possíveis valores de x que podem ser aplicados para dar uma solução real. O intervalo de uma função consiste nos valores de y que retornarão. Para determinar o domínio da função, procure valores que produzam um resultado matematicamente impossível. Você então indica o domínio se todos os outros valores de x. Para encontrar o intervalo, considere os valores de y em pontos de fronteira arbitrários e observe o comportamento da função.
 . Não há limitação nos valores permitidos de x para esta equação. No entanto, você deve perceber que esta é a equação de uma parábola, com x = 0 como seu centro, e uma parábola não é uma função porque não é uma comparação um-para-um dos valores de x e y. Para limitar esta equação e torná-la uma função, para a qual podemos encontrar uma inversa, precisamos definir o domínio como x≥0.
. Não há limitação nos valores permitidos de x para esta equação. No entanto, você deve perceber que esta é a equação de uma parábola, com x = 0 como seu centro, e uma parábola não é uma função porque não é uma comparação um-para-um dos valores de x e y. Para limitar esta equação e torná-la uma função, para a qual podemos encontrar uma inversa, precisamos definir o domínio como x≥0. , será sempre positivo ou 0, para qualquer valor de x. Então, se a equação somar +2, o intervalo será qualquer valor y≥2.
, será sempre positivo ou 0, para qualquer valor de x. Então, se a equação somar +2, o intervalo será qualquer valor y≥2.
4. Troque os papéis dos termos x e y. Sem alterar a equação de qualquer outra forma, você deve substituir todas as formas de y por x, e todas as formas de x por y. Este é o passo que realmente `inverte` a equação.
 , este passo de inversão resultará na nova equação de
, este passo de inversão resultará na nova equação de  .
. ou
ou  para indicar a função inversa.
para indicar a função inversa.
5. Reescreva a equação inversa em termos de y. Usando uma combinação de etapas algébricas e certificando-se de que a mesma operação seja realizada em ambos os lados da equação, você precisará isolar a variável y. Para a comparação  , esta revisão fica assim:
, esta revisão fica assim:
 , esta revisão fica assim:
, esta revisão fica assim: (premissa original)
(premissa original) (subtrair 2 de ambos os lados)
(subtrair 2 de ambos os lados) (dividir ambos os lados por 2)
(dividir ambos os lados por 2) (raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada resulta em respostas possíveis positivas e negativas)
(raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada resulta em respostas possíveis positivas e negativas)
6. Determine o domínio e a imagem da função inversa. Como no início, examine a equação invertida para determinar o domínio e a imagem. Com duas soluções possíveis, escolha a solução que tem domínio e imagem que são o inverso do domínio e imagem originais.
 . Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser
. Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser  seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥2. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥0, se você pegar a solução positiva da raiz quadrada, ou y≤0, se você pegar a solução negativa de a raiz quadrada. Observe que para encontrar a função inversa, você originalmente definiu o domínio como x≥0. Portanto, a solução correta para a função inversa é a opção positiva.
seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥2. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥0, se você pegar a solução positiva da raiz quadrada, ou y≤0, se você pegar a solução negativa de a raiz quadrada. Observe que para encontrar a função inversa, você originalmente definiu o domínio como x≥0. Portanto, a solução correta para a função inversa é a opção positiva. , o domínio foi definido como todos os valores de x≥0, e o intervalo foi definido como todos os valores de y≥2. Para a função inversa, agora esses valores trocam, e o domínio são todos os valores de x≥2, e o intervalo são todos os valores de y≥0.
, o domínio foi definido como todos os valores de x≥0, e o intervalo foi definido como todos os valores de y≥2. Para a função inversa, agora esses valores trocam, e o domínio são todos os valores de x≥2, e o intervalo são todos os valores de y≥0.
7. Verifique se sua função inversa funciona. Para ter certeza de que seu trabalho está correto e sua inversa é a equação correta, escolha qualquer valor para x e coloque-o na equação original para encontrar y. Em seguida, coloque esse valor de y no lugar de x em sua equação inversa e veja se você obtém o número com o qual começou. Se sim, sua função inversa está correta.
 . Isso dá o resultado y = 4.
. Isso dá o resultado y = 4. . Isso realmente dá o resultado y = 1. Você pode concluir que sua função inversa está correta.
. Isso realmente dá o resultado y = 1. Você pode concluir que sua função inversa está correta.Método 2 de 3: Completando o quadrado para encontrar a função inversa

1. Dê a equação quadrática a forma correta. Para encontrar a inversa, você tem que começar com a equação da forma  . Se necessário, você precisa combinar termos semelhantes para obter a equação neste formato. Com a equação escrita desta forma, você pode contar um pouco mais sobre ela.
. Se necessário, você precisa combinar termos semelhantes para obter a equação neste formato. Com a equação escrita desta forma, você pode contar um pouco mais sobre ela.
 . Se necessário, você precisa combinar termos semelhantes para obter a equação neste formato. Com a equação escrita desta forma, você pode contar um pouco mais sobre ela.
. Se necessário, você precisa combinar termos semelhantes para obter a equação neste formato. Com a equação escrita desta forma, você pode contar um pouco mais sobre ela. - A primeira coisa que você notará é o valor do coeficiente a. se um>0, então a equação define uma parábola cujas extremidades apontam para cima (parábola do vale). se um<0, então a equação define uma parábola cujas extremidades apontam para baixo (parábola da montanha). Observe que a≠0. Se não fosse, esta seria uma função linear e não uma quadrática.

2. Reconhecer o formato padrão da quadrática. Antes de encontrar a função inversa, você precisa reescrever a equação no formato padrão. O formato padrão para uma função quadrática é  . Os termos numéricos a, h e k serão avaliados se você transformar a equação calculando o quadrado.
. Os termos numéricos a, h e k serão avaliados se você transformar a equação calculando o quadrado.
 . Os termos numéricos a, h e k serão avaliados se você transformar a equação calculando o quadrado.
. Os termos numéricos a, h e k serão avaliados se você transformar a equação calculando o quadrado. , que é então modificado pelos outros dois elementos a e k. Para chegar a esta forma quadrática perfeita, você terá que criar certas condições em sua equação quadrática.
, que é então modificado pelos outros dois elementos a e k. Para chegar a esta forma quadrática perfeita, você terá que criar certas condições em sua equação quadrática.
3. Pense na forma de uma função quadrática perfeita. Lembre-se de que uma função quadrática que é um quadrado perfeito surge de dois binômios de  , ou
, ou  . Se você fizer essa multiplicação, obterá
. Se você fizer essa multiplicação, obterá  . Então o primeiro termo da quadrática é o primeiro termo do binômio, quadrado, e o último termo da quadrática é o quadrado do segundo termo do binômio. O termo médio consiste em duas vezes o produto dos dois termos, neste caso
. Então o primeiro termo da quadrática é o primeiro termo do binômio, quadrado, e o último termo da quadrática é o quadrado do segundo termo do binômio. O termo médio consiste em duas vezes o produto dos dois termos, neste caso  .
.
 , ou
, ou  . Se você fizer essa multiplicação, obterá
. Se você fizer essa multiplicação, obterá  . Então o primeiro termo da quadrática é o primeiro termo do binômio, quadrado, e o último termo da quadrática é o quadrado do segundo termo do binômio. O termo médio consiste em duas vezes o produto dos dois termos, neste caso
. Então o primeiro termo da quadrática é o primeiro termo do binômio, quadrado, e o último termo da quadrática é o quadrado do segundo termo do binômio. O termo médio consiste em duas vezes o produto dos dois termos, neste caso  .
. e um segundo termo x. Do coeficiente desse termo, que você pode definir como `2b`, você deve obter
e um segundo termo x. Do coeficiente desse termo, que você pode definir como `2b`, você deve obter  ver para encontrar. Isso requer uma combinação de dividir por dois e, em seguida, elevar ao quadrado esse resultado.
ver para encontrar. Isso requer uma combinação de dividir por dois e, em seguida, elevar ao quadrado esse resultado.
4. Certifique-se de que o coeficiente de X 2  1 é. Você se lembra da forma original da função quadrática
1 é. Você se lembra da forma original da função quadrática  . Se o primeiro coeficiente for diferente de 1, você precisará dividir todos os termos por esse valor para obter a = 1.
. Se o primeiro coeficiente for diferente de 1, você precisará dividir todos os termos por esse valor para obter a = 1.
 1 é. Você se lembra da forma original da função quadrática
1 é. Você se lembra da forma original da função quadrática  . Se o primeiro coeficiente for diferente de 1, você precisará dividir todos os termos por esse valor para obter a = 1.
. Se o primeiro coeficiente for diferente de 1, você precisará dividir todos os termos por esse valor para obter a = 1. . Você pode simplificar isso dividindo todos os termos por 2 para obter a função resultante
. Você pode simplificar isso dividindo todos os termos por 2 para obter a função resultante  para obter. O coeficiente 2 fica fora dos colchetes e fará parte da sua solução final.
para obter. O coeficiente 2 fica fora dos colchetes e fará parte da sua solução final. será simplificado para
será simplificado para  . Calcule as frações com cuidado.
. Calcule as frações com cuidado.
5. Encontre metade do coeficiente do meio e eleve ao quadrado. Você já tem os dois primeiros termos da fórmula quadrática. Estes são o termo  e o coeficiente que representa o termo x. Tomando esse coeficiente como o valor que ele tem, você pode adicionar ou subtrair o número necessário para fazer um quadrado perfeito. Lembre-se de que o terceiro termo necessário do quadrado é esse segundo coeficiente dividido por dois e depois elevado ao quadrado.
e o coeficiente que representa o termo x. Tomando esse coeficiente como o valor que ele tem, você pode adicionar ou subtrair o número necessário para fazer um quadrado perfeito. Lembre-se de que o terceiro termo necessário do quadrado é esse segundo coeficiente dividido por dois e depois elevado ao quadrado.
 e o coeficiente que representa o termo x. Tomando esse coeficiente como o valor que ele tem, você pode adicionar ou subtrair o número necessário para fazer um quadrado perfeito. Lembre-se de que o terceiro termo necessário do quadrado é esse segundo coeficiente dividido por dois e depois elevado ao quadrado.
e o coeficiente que representa o termo x. Tomando esse coeficiente como o valor que ele tem, você pode adicionar ou subtrair o número necessário para fazer um quadrado perfeito. Lembre-se de que o terceiro termo necessário do quadrado é esse segundo coeficiente dividido por dois e depois elevado ao quadrado. você encontra o terceiro termo necessário dividindo 3 por 2 (ou 3/2), e então elevando ao quadrado, para obter 9/4. O quadrático
você encontra o terceiro termo necessário dividindo 3 por 2 (ou 3/2), e então elevando ao quadrado, para obter 9/4. O quadrático  é um quadrado perfeito.
é um quadrado perfeito. são. Metade do termo médio é -2, e então você eleva ao quadrado para obter 4. O quadrado perfeito resultante é
são. Metade do termo médio é -2, e então você eleva ao quadrado para obter 4. O quadrado perfeito resultante é  .
.
6. Adicionar e subtrair do terceiro termo necessário ao mesmo tempo. Este é um conceito complicado, mas funciona. Adicionar e subtrair o mesmo número em lugares diferentes da sua função não altera o valor da função. No entanto, ao fazer isso, você obterá sua função na forma adequada.
 . Como mencionado acima, você usa os dois primeiros termos para completar o quadrado. Usando o termo médio de -4x, você gera um terceiro termo +4. Adicione 4 e subtraia 4 da equação, na forma
. Como mencionado acima, você usa os dois primeiros termos para completar o quadrado. Usando o termo médio de -4x, você gera um terceiro termo +4. Adicione 4 e subtraia 4 da equação, na forma  . Os parênteses são colocados apenas para definir a equação quadrática que você está fazendo. Observe o +4 dentro dos colchetes e o -4 do lado de fora. Simplifique os números para o resultado
. Os parênteses são colocados apenas para definir a equação quadrática que você está fazendo. Observe o +4 dentro dos colchetes e o -4 do lado de fora. Simplifique os números para o resultado  .
.
7. Fatore a equação quadrática. O polinômio entre parênteses é uma equação quadrática, que você pode reescrever como  . No exemplo da etapa anterior (
. No exemplo da etapa anterior ( ) você fatora o fator quadrático em
) você fatora o fator quadrático em  . Copie o resto da equação para que sua solução
. Copie o resto da equação para que sua solução  está se tornando. Esta é a mesma função que sua equação quadrática original (
está se tornando. Esta é a mesma função que sua equação quadrática original ( ), reescrito como a forma padrão
), reescrito como a forma padrão  .
.
 . No exemplo da etapa anterior (
. No exemplo da etapa anterior ( ) você fatora o fator quadrático em
) você fatora o fator quadrático em  . Copie o resto da equação para que sua solução
. Copie o resto da equação para que sua solução  está se tornando. Esta é a mesma função que sua equação quadrática original (
está se tornando. Esta é a mesma função que sua equação quadrática original ( ), reescrito como a forma padrão
), reescrito como a forma padrão  .
.
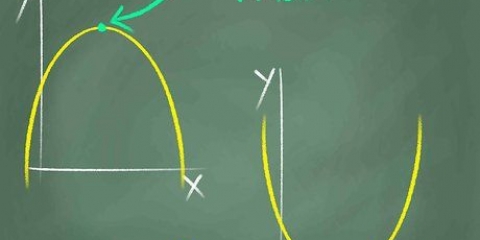
8. Defina o domínio e o escopo da função. O domínio é o conjunto de valores x que podem ser usados como entradas para a função. O intervalo é o conjunto de valores y que podem ser o resultado. Lembre-se de que uma parábola não é uma função com uma inversa definível, porque não existe uma relação um-para-um entre os valores x e y, devido à simetria da parábola. Para resolver este problema, você deve definir o domínio como todos os valores de x que são maiores que x=h, o vértice da parábola.
 . Como este está no formato padrão, você pode determinar o vértice como x=2, y=5. Então para evitar a simetria, você só trabalha com o lado direito do gráfico, e define o domínio se todos os valores x≥2. Inserir o valor x=2 na função retorna y=5. Você pode ver que os valores de y aumentarão à medida que x aumenta. Portanto, o alcance desta equação é y≥5.
. Como este está no formato padrão, você pode determinar o vértice como x=2, y=5. Então para evitar a simetria, você só trabalha com o lado direito do gráfico, e define o domínio se todos os valores x≥2. Inserir o valor x=2 na função retorna y=5. Você pode ver que os valores de y aumentarão à medida que x aumenta. Portanto, o alcance desta equação é y≥5.
9. Troque os valores x e y. Este é o passo onde você começa encontrando a forma inversa da equação. Deixe a equação em sua totalidade, exceto trocando essas variáveis.
 . Insira x no lugar de f(x), e insira y (ou f(x), se preferir) no lugar de x. Isso dá como uma nova função
. Insira x no lugar de f(x), e insira y (ou f(x), se preferir) no lugar de x. Isso dá como uma nova função  .
.
10. Reescreva a equação inversa em termos de y. Usando uma combinação de etapas algébricas, certificando-se de realizar a mesma operação uniformemente em ambos os lados da equação, isole a variável y. Para a comparação de trabalho  esta revisão fica assim:
esta revisão fica assim:
 esta revisão fica assim:
esta revisão fica assim: (ponto de partida original)
(ponto de partida original) (subtrair 5 de ambos os lados)
(subtrair 5 de ambos os lados) (raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada produz respostas possíveis positivas e negativas)
(raiz quadrada de ambos os lados; lembre-se de que a raiz quadrada produz respostas possíveis positivas e negativas) (adicione 2 em ambos os lados)
(adicione 2 em ambos os lados)
11. Determine o domínio e a imagem da função inversa. Como no início, examine a equação inversa para determinar o domínio e a imagem. Com duas soluções possíveis, escolha a solução que tem domínio e imagem que são o inverso do domínio e imagem originais.
 . Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser
. Como a função raiz quadrada não é definida para valores negativos, o termo . deve ser  seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥5. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥2 (se você pegar a solução positiva da raiz quadrada), ou y≤2 (se você escolher a solução negativa da raiz quadrada). Lembre-se que você originalmente definiu o domínio como x≥2, para encontrar a função inversa. Portanto, a solução correta para a função inversa é a opção positiva.
seja sempre positivo. Portanto, os valores permitidos de x (o domínio) devem ser x≥5. Com isso como domínio, os valores resultantes de y (o intervalo) são todos os valores y≥2 (se você pegar a solução positiva da raiz quadrada), ou y≤2 (se você escolher a solução negativa da raiz quadrada). Lembre-se que você originalmente definiu o domínio como x≥2, para encontrar a função inversa. Portanto, a solução correta para a função inversa é a opção positiva.
12. Verifique se sua função inversa funciona. Para ter certeza de que seu trabalho está correto e sua inversa é a equação correta, escolha qualquer valor para x e coloque-o na equação original para encontrar y. Em seguida, coloque esse valor de y no lugar de x em sua equação inversa e veja se você obtém o número com o qual começou. Se sim, então sua função inversa está correta.
 processar. Isso dá o resultado y = 6.
processar. Isso dá o resultado y = 6. . Isso retorna y=3, que é o número com o qual você começou. Você pode concluir que sua função inversa está correta.
. Isso retorna y=3, que é o número com o qual você começou. Você pode concluir que sua função inversa está correta.Método 3 de 3: Usando a fórmula quadrada

1. Use a fórmula quadrática para resolver x. Lembre-se, ao resolver equações quadráticas, existe um método para fatorá-las (se possível). Se a fatoração não funcionasse, você poderia usar a fórmula quadrada, que daria as soluções reais para qualquer equação quadrática. Você também pode usar a fórmula quadrada como um método para encontrar funções inversas.
- A fórmula quadrada é x=[-b±√(b^2-4ac)]/2a.
- Observe que a fórmula quadrada produz duas soluções possíveis, uma positiva e uma negativa. Você fará essa escolha com base na determinação do domínio e escopo da função.

2. Comece com uma equação quadrática para encontrar a inversa. Sua equação quadrática deve começar no formato  . Siga os passos algébricos necessários para obter sua equação nessa forma.
. Siga os passos algébricos necessários para obter sua equação nessa forma.
 . Siga os passos algébricos necessários para obter sua equação nessa forma.
. Siga os passos algébricos necessários para obter sua equação nessa forma. .
.
3. Plote a equação para determinar o domínio e o intervalo. Faça o gráfico da função, usando uma calculadora gráfica ou plotando vários pontos até que você possa desenhar a parábola. Você verá que esta equação define uma parábola com o ponto mais alto em (-1,-4). Então para definir isso como uma função que terá uma inversa, você define o domínio como todos os valores de x≤-1. O intervalo é então todos os valores y≥-4.

4. Troque as variáveis x e y. Para encontrar o inverso, troque as variáveis x e y. Deixe a equação inalterada, exceto trocar as variáveis. Neste estágio, substitua x por f(x).
 , isso dá o resultado
, isso dá o resultado  .
.
5. Defina o lado esquerdo da equação igual a zero. Lembre-se que para usar a fórmula quadrática você tem que definir a equação igual a zero, então use os coeficientes na fórmula. Da mesma forma, este método de encontrar uma função inversa começa definindo a equação igual a zero.
 .
.
6. Redefina as variáveis para ajustar a fórmula quadrada. Este passo é um pouco complicado. Saiba que a fórmula quadrada resolve para x, na equação  . Então, para a equação que você tem agora,
. Então, para a equação que você tem agora,  , para estar em conformidade com essa classificação, você deve redefinir os termos da seguinte forma:
, para estar em conformidade com essa classificação, você deve redefinir os termos da seguinte forma:
 . Então, para a equação que você tem agora,
. Então, para a equação que você tem agora,  , para estar em conformidade com essa classificação, você deve redefinir os termos da seguinte forma:
, para estar em conformidade com essa classificação, você deve redefinir os termos da seguinte forma: . Então, x = 1
. Então, x = 1 . Então, b = 2
. Então, b = 2 . Então, c=(-3-x)
. Então, c=(-3-x)
7. Resolva a fórmula quadrada com esses valores redefinidos. Normalmente você processaria os valores de a, b e c na fórmula quadrada para resolver x. No entanto, lembre-se de que você trocou x e y anteriormente para encontrar o da função inversa. Então, quando você usa a fórmula quadrada para resolver x, na verdade está resolvendo y, ou o inverso de f. Os passos para resolver a fórmula quadrada funcionam da seguinte forma:

8. Escreva as duas soluções possíveis. Observe que a fórmula quadrada fornece dois resultados possíveis, usando o símbolo ±. Escreva as duas soluções separadas para facilitar a determinação do domínio e da imagem e forneça a solução final correta. Essas duas soluções são:



9. Determine o domínio e a imagem da função inversa. Observe que para definir a raiz quadrada, o domínio deve ser x≥-4. Lembre-se de que o domínio da função original era x≤-1 e o intervalo era y≥-4. Para escolher a função inversa que corresponde, você precisa da segunda solução,  escolha como a função inversa correta.
escolha como a função inversa correta.
 escolha como a função inversa correta.
escolha como a função inversa correta.
10. Verifique se sua função inversa está correta. Para ter certeza de que seu trabalho está correto e sua inversa é a equação correta, escolha qualquer valor para x e coloque-o na equação original para encontrar y. Em seguida, coloque esse valor de y no lugar de x em sua equação inversa e veja se você obtém o número com o qual começou. Se sim, então sua função inversa está correta.
 , escolha seu x=-2. Isso retorna y=-3. Agora substitua o valor de x=-3 na função inversa,
, escolha seu x=-2. Isso retorna y=-3. Agora substitua o valor de x=-3 na função inversa,  . Isso retorna -2, que é de fato o valor com o qual você começou. Então sua definição da função inversa está correta.
. Isso retorna -2, que é de fato o valor com o qual você começou. Então sua definição da função inversa está correta.Artigos sobre o tópico "Encontrando a inversa de uma equação quadrática"
Оцените, пожалуйста статью
Similar
Popular