Por exemplo, suponha que você tenha a equação 3X + -2X + 14X=0. Por um X fora dos parênteses, obtemos X(3X + -2X + 14)=0. 
Em nossa declaração de exemplo, preenchemos nossos valores a, b e c (respectivamente 3, -2 e 14) na equação quadrática em: Resposta 1: Resposta 2: 
A razão pela qual isso funciona tem a ver com o fato fundamental de que qualquer número multiplicado por zero é igual a zero. Quando você converte a equação para a forma X(Machado + bx + c)=0, você basicamente divide os dois em partes: uma parte é o X-variável fora dos parênteses e a outra é o quadrado dentro dos parênteses. Se qualquer uma dessas partes é igual a zero, então toda a equação também é. Então, se as duas respostas para o quadrado dentro dos parênteses fazem essa parte zero, então as respostas para a equação cúbica também tornarão a parte fora dos parênteses igual a zero. 

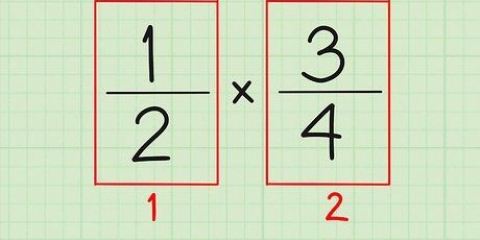
Em nossa declaração de exemplo, uma=2 e d=6. Os fatores de 2 são 1 e 2. Os fatores de 6 são 1, 2, 3 e 6. 
Em nossa equação você calcula os fatores de uma (1, 2) sobre os fatores de d (1, 2, 3, 6) e você obtém a seguinte lista: 1, 1/2, 1/3, 1/6, 2 e 2/3. Agora adicionamos os números negativos à lista para completá-la: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 e -2/3. A solução inteira da nossa equação cúbica pode ser encontrada em algum lugar nesta lista. 
O compartilhamento sintético é um tópico complexo - siga o link acima para obter mais informações. Aqui está um exemplo de como encontrar uma das soluções para nossa equação cúbica usando divisão sintética: 

Em nosso problema de exemplo, resolvemos isso da seguinte forma: 
Em nosso problema de exemplo, resolvemos isso da seguinte forma: 
Em nosso problema de exemplo, determinar Δ é muito simples, porque tanto Δ0 quanto Δ1=0. Resolvemos isso da seguinte forma: 
Em nosso problema de exemplo, encontramos C do seguinte modo: 
Em nosso problema de exemplo, podemos resolver isso verificando a resposta quando n é igual a 1, 2 ou 3. As respostas que obtemos desses testes são as possíveis respostas para nossa equação cúbica - qualquer solução que produz 0 após a substituição na equação está correta. Por exemplo, suponha que obtemos 1 em resposta a um dos testes, porque inserir 1 em X - 3X + 3X - 1 resulta em 0 se resposta, então 1 uma das respostas para nossa equação cúbica.
Resolvendo uma equação cúbica
Contente
A primeira vez que você encontrar uma equação cúbica (da forma Machado + bx + cx + d=0) pode parecer quase insolúvel. No entanto, este método de resolver equações cúbicas existe há séculos! Foi descoberto no século XVI pelos matemáticos italianos Niccolò Tartaglia e Gerolamo Cardano. Foi uma das primeiras fórmulas desconhecidas dos antigos gregos e romanos. Resolver equações cúbicas pode ser muito difícil, mas com a abordagem correta (e conhecimento básico suficiente), mesmo as equações cúbicas mais complicadas podem ser domadas.
Degraus
Método 1 de 3: Resolvendo com a fórmula abc

1. Verifique se a equação cúbica contém uma constante. Como indicado acima, as equações cúbicas têm a forma Machado + bx + cx + d=0. b, c, e d pode ser 0 sem alterar se é ou não uma equação cúbica - essencialmente significando que uma equação não precisa consistir em todos os termos bx, cx ou d ser uma equação cúbica. Você começa a aplicar este método relativamente simples de resolver equações cúbicas verificando primeiro se sua equação tem uma constante (uma d-onde o). É isto não é o caso, então você pode des fórmula abc para encontrar as respostas da equação com um pouco de matemática.
- Se a equação contiver uma constante, você terá que usar um método diferente. Veja abaixo abordagens alternativas.

2. dissolver um X fora da equação. Como sua equação não contém uma constante, cada termo na equação tem um X-variável. Isso significa que um X pode ser fatorado fora da equação para simplificá-la. Faça isso e reescreva sua equação na forma X(Machado + bx + c).

3. Use a fórmula abc para resolver os termos entre parênteses. Você deve ter notado que os termos de sua nova equação entre parênteses estão na forma de uma equação quadrática (Machado + bx + c). Isso significa que podemos encontrar os valores para os quais a equação quadrática é igual a zero por a, b e c na fórmula abc ({-b +/-√ (b- 4ac)}/2uma). Isso encontrará duas das respostas da sua equação cúbica.
- {-b +/-√ (b- 4ac)}/2uma
- {-(-2) +/-√ ((-2)-4(3)(14))}/2(3)
- {2 +/-√ (4 - (12)(14))}/6
- {2 +/-√ (4 - (168)}/6
- {2 +/-√ (-164)}/6
- {2 + √(-164)}/6
- {2 + 12.8eu}/6
- {2 - 12.8eu}/6

4. Use zero e as respostas quadráticas como respostas para sua equação cúbica. As equações quadrilaterais têm duas soluções, mas as equações cúbicas têm três. Você já tem dois - estas são as respostas que você encontrou ao elaborar a "equação quadrática" entre parênteses. Nos casos em que uma equação é apropriada para este `fora de parênteses`, a terceira resposta será sempre 0 são. Parabéns - você acabou de resolver uma equação cúbica.
Método 2 de 3: Resolvendo usando listas de fatores

1. Certifique-se de que sua equação cúbica tenha uma constante. Embora o método acima seja útil porque não exige que você aprenda novas habilidades matemáticas, nem sempre funcionará para resolver equações cúbicas. Se sua equação estiver na forma Machado + bx + cx + d=0 estado, e d for diferente de zero, os parênteses não funcionarão e você precisará deste método ou do da próxima parte.
- Por exemplo, suponha que você tenha a equação 2 dadaX + 9X + 13X=-6. Nesse caso, um 0 à direita do sinal de igual exigirá a adição de 6 a ambos os lados. Nossa nova equação é 2X + 9X + 13X + 6=0, d=6, então não podemos usar os parênteses da parte anterior.

2. Determine os fatores de uma e d. Para resolver a equação cúbica, comece determinando os fatores de uma (o coeficiente de X termos d (a constante no final da equação). Como lembrete, os fatores são aqueles números que multiplicados juntos formam outro número. Por exemplo, porque seu 6 surge da multiplicação 6 &Tempo; 1 e 2 × 3, são 1, 2, 3 e 6 fatores de 6.

3. Compartilhe os fatores de uma pelos fatores de d. Agora você lista todos os valores que obtém dividindo cada fator uma por qualquer fator d. Isso geralmente resulta em muitas frações e alguns números inteiros. As soluções inteiras de sua equação cúbica serão um dos inteiros da lista ou o número negativo de um desses números.

4. Use o compartilhamento sintético para verificar manualmente suas respostas. Depois de reunir a lista de valores, você pode encontrar as soluções inteiras para sua equação cúbica digitando manualmente cada número inteiro e verificando quais são iguais a zero. Se você não quer perder tempo com isso, existe um método um pouco mais rápido de acordo com uma técnica chamada compartilhamento sintético. A essência é que você divide os inteiros pelo original a, b, c e d coeficientes da sua equação cúbica. Se você ficar com um resto de 0, seu valor é uma das soluções da equação cúbica.
- -1 | 2 9 13 6
- __| -2-7-6
- __| 2 7 6 0
- Como acabamos com 0 como resto, sabemos que uma das soluções de nossa equação cúbica é o inteiro -1 é.
Método 3 de 3: usando o `discriminante`

1. Escreva os valores de a, b, c e d. Neste método de encontrar as soluções de uma equação cúbica, dependeremos muito dos coeficientes dos termos em nossa equação. Por esta razão, é aconselhável usar os termos a, b, c e d anote antes de começar para não esquecer o que é cada um.
- Por exemplo, para a comparação X - 3X + 3X - 1, escrevemos uma=1, b=-3, c=3 e d=-1. Não se esqueça disso de um X-variável sem coeficiente assume-se que o coeficiente é igual a 1.

2. Calcule Δ0=b - 3ac. Ao usar o discriminante para resolver equações cúbicas, você precisa de um pouco mais de matemática avançada, mas se você seguir o procedimento com cuidado, verá que ele é uma ferramenta valiosa para resolver aquelas já complicadas equações cúbicas. Comece encontrando Δ0, o primeiro de vários valores importantes que precisamos, substituindo os valores apropriados na fórmula b - 3ac.
- b - 3ac
- (-3) - 3(1)(3)
- 9 - 3(1)(3)
- 9 - 9=0=Δ0

3. Calcular Δ1=2b - 9abc + 27umad. A próxima quantidade importante que precisamos, Δ1, requer um pouco mais de trabalho, mas pode ser encontrada da mesma maneira que Δ0. Substitua os valores corretos na fórmula 2b - 9abc + 27umad para o valor de Δ1.
- 2(-3) - 9(1)(-3)(3) + 27(1)(-1)
- 2(-27) - 9(-9) + 27(-1)
- -54 + 81 - 27
- 81 - 81=0=Δ1

4. Calcular Δ=Δ1 - 4Δ0) ÷ -27uma. Então calculamos o discriminante da equação cúbica dos valores para Δ0 e Δ1. Um discriminante é simplesmente um número que nos diz algo sobre as respostas de um polinômio (inconscientemente você já deve conhecer o discriminante quadrático: b - 4ac). No caso da equação cúbica, se o discriminante é positivo, então a equação tem três soluções reais. Se o discriminante é zero, então a equação tem uma ou duas soluções reais, e algumas dessas soluções são compartilhadas. Se for negativo, então a equação tem apenas uma solução. (Uma equação cúbica sempre tem uma solução real, porque o gráfico é sempre pelo menos uma vez com a X-cortes de eixo.)
- Δ1 - 4Δ0) ÷ -27uma
- (0) - 4(0)) -27(1)
- 0 - 0 27
- 0=Δ, então nossa equação tem 1 ou 2 respostas.

5. calcular C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). O último valor importante a ser calculado é C. Com esta quantidade importante, podemos finalmente encontrar as três soluções. Resolva isso como de costume, substituindo Δ1 e Δ0 quando necessário.
- √(√((Δ1 - 4Δ0) + Δ1)/ 2)
- √(√((0 - 4(0)) + (0))/ 2)
- √(√((0 - 0) + (0))/ 2)
- 0=C

6. Calcule as três respostas com suas variáveis. As respostas para sua equação cúbica são dadas pela fórmula (b + uC + (Δ0/uC)) / 3uma, através do qual vocês=(-1 + √(-3))/2 e n é 1, 2 ou 3. Digite seus valores quando necessário para resolver isso - isso requer muita matemática, mas deve fornecer três respostas possíveis!
Artigos sobre o tópico "Resolvendo uma equação cúbica"
Оцените, пожалуйста статью
Popular