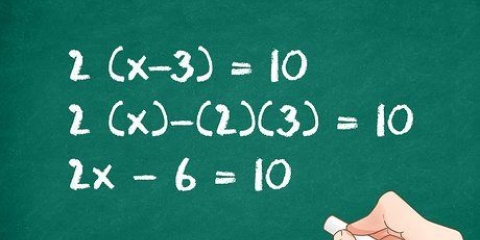4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 √(2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

√(2x+9) - 5 = 0 √(2(8)+9) - 5 = 0 √(16+9) - 5 = 0 √(25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(Para x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (para x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Resolva x em uma equação
Contente
Existem várias maneiras de resolver x em uma equação, se você está trabalhando com expoentes e raízes ou simplesmente precisa dividir ou multiplicar. Seja qual for o método usado, você deve sempre encontrar uma maneira de isolar x de um lado da equação para poder calcular o valor. Veja como fazer isso:
Degraus
Método 1 de 5: Usando uma Equação Linear Ordinária

1. Anote o problema. Aqui está a atribuição:
- 2(x+3) + 9 - 5 = 32

2. Calcule o expoente. Lembre-se da ordem das operações: HMVDOA, que significa Parênteses, Exponenciação, Divisão/Multiplicação, Adição/Subtração. Nesse caso, você não pode descobrir o que está entre parênteses primeiro porque o x pertence a ele, então você começa com a potência, 2. 2 = 4

3. Faça a multiplicação. Multiplique 4 por (x+3). Veja como:

4. Agora faça a adição e a subtração. Basta adicionar ou subtrair os números restantes. Veja como:

5. Isolar a variável. Você faz isso dividindo ambos os lados da equação por 4 para encontrar x. 4x/4 = x e 16/4 = 4, então x = 4.

6. Confira seu cálculo. Substitua x = 4 de volta na equação original para ter certeza de que está correta. Veja como:
Método 2 de 5: com exponenciação

1. Anote o problema. Vamos supor que você esteja trabalhando em um problema em que o termo x também contém um expoente:
- 2x + 12 = 44

2. Isolar o termo com o expoente. A primeira coisa que você deve fazer agora é combinar termos semelhantes para que todas as constantes fiquem no lado direito da equação, enquanto o termo com o expoente está no lado esquerdo. Basta subtrair 12 de ambos os lados. Veja como:

3. Isole a variável com o expoente, dividindo ambos os lados pelo coeficiente do termo x. Neste caso, 2 é o coeficiente x, o que significa que ambos os lados devem ser divididos por 2 para eliminá-lo. Veja como:

4. Tire a raiz quadrada de cada lado da equação. Ao calcular a raiz quadrada de x, você fica com x à esquerda e a raiz quadrada de 16,4, à direita. Então, x = 4.

5. Confira seu cálculo. Substitua x = 4 de volta na equação original para ter certeza de que está correta. Veja como:
Método 3 de 5: Use Frações

1. Anote o problema. Vamos supor que você esteja lidando com o seguinte problema:
- (x + 3)/6 = 2/3

2. Multiplicação cruzada. Para multiplicar transversalmente, multiplique o denominador de cada fração pelo numerador da outra fração. Então, multiplique 6 (o primeiro denominador) por 2 (o segundo numerador), para obter 12 no lado direito da equação.Em seguida, multiplique 3 (o segundo denominador) por x + 3 (o primeiro numerador), para obter 3 x + 9 à esquerda da equação. Veja como será:

3. Combinar termos semelhantes. Combine as constantes na equação subtraindo 9 de ambos os lados da equação. Aqui está o que fazer:

4. Isolar x dividindo cada termo pelo coeficiente x. Basta dividir 3x e 9 por 3, o coeficiente de x, e resolver para x. 3x/3 = x e 3/3 = 1, então você fica com x = 1.

5. Confira seu cálculo. Para verificar seu trabalho, substitua x de volta na equação original para ter certeza de que está correto. Aqui está o que fazer:
Método 4 de 5: usando caracteres raiz

1. Anote o problema. Vamos supor que você resolva x no seguinte problema:
- √(2x+9) - 5 = 0

2. Isolar a raiz quadrada. Você deve isolar a parte da raiz quadrada da equação à esquerda da equação antes de continuar. Então você adiciona 5 a ambos os lados da equação. Veja como:

3. Desenhe a raiz quadrada de ambos os lados. Assim como você divide ambos os lados de uma equação pelo coeficiente multiplicado por x, você também deve tirar a raiz quadrada de ambos os lados de uma equação se x estiver abaixo do sinal do radical. Isso remove o radical da equação. Veja como fazer isso:

4. Combinar termos semelhantes. Combine termos iguais subtraindo 9 de ambos os lados da equação para que todas as constantes fiquem à direita, enquanto x permanece à esquerda. Aqui está o que fazer:

5. Isolar a variável. A última coisa a fazer para resolver x é isolar a variável dividindo ambos os lados da equação por 2, o coeficiente do termo x. 2x/2 = x e 16/2 = 8, então você fica com x = 8.

6. Confira seu cálculo. Digite 8 na equação novamente para x para verificar se seu cálculo está correto:
Método 5 de 5: use o valor absoluto

1. Anote o problema. Vamos supor que você esteja tentando resolver x no seguinte problema:
- |4x +2| - 6 = 8

2. Isolar o valor absoluto. A primeira coisa a fazer é combinar termos semelhantes e isolar o valor absoluto. Nesse caso, você pode fazer isso adicionando 6 a ambos os lados da equação. Veja como:

3. Remova o valor absoluto e resolva a equação. Este é o primeiro e mais fácil passo. Agora você tem que resolver x duas vezes, cada vez que trabalhar com um valor absoluto. Veja como fazer isso pela primeira vez:

4. Remova o valor absoluto e altere o sinal dos termos do outro lado do sinal de igual antes de continuar a resolver. Agora faça isso novamente, desta vez tornando a parte esquerda da equação igual a -14 em vez de 14. Veja como:

5. Confira seu cálculo. Agora que você sabe que x = (3, -4), basta substituir os dois números de volta na equação para ter certeza de que está correto. Veja como:
Pontas
- Para verificar seu trabalho, insira o valor de x de volta na equação original e resolva-o.
- As raízes são outra maneira de representar expoentes.A raiz quadrada de x = x^1/2.
Artigos sobre o tópico "Resolva x em uma equação"
Оцените, пожалуйста статью
Similar
Popular