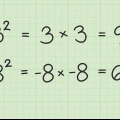Dividindo raízes quadradas

Contente

Degraus
Pontas
Avisos

Dividir por raízes quadradas é essencialmente a simplificação de uma fração. Claro que a presença de raízes quadradas torna o processo um pouco mais complicado, mas existem regras que nos permitem trabalhar com frações de forma relativamente fácil. A coisa mais importante a lembrar é que você precisa dividir coeficientes por coeficientes e raízes por raízes. Você também nunca deve deixar uma raiz quadrada em um denominador.

Degraus

Método 1 de 4: Compartilhando cenouras

Imagem intitulada Divide Square Roots Step 1

1. Configure a fração. Se a expressão ainda não estiver na forma de uma fração, reescreva-a assim. Isso torna mais fácil seguir todas as etapas necessárias para dividir por uma raiz quadrada. Lembre-se que um caractere de divisão é o mesmo que uma barra de fração.

Por exemplo, se você $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ calcula e, em seguida, reescreva o problema como: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Imagem intitulada Divide Square Roots Step 2

2. Use um sinal de radical. Se o seu problema tem uma raiz quadrada no numerador e no denominador, você pode colocar ambas as raízes sob um radical. (Uma raiz é o número sob o radical.) Isso torna a simplificação ainda mais fácil.

Por exemplo,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ pode ser reescrito como

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Imagem intitulada Divide Square Roots Step 3

3. Divida as raízes. Divida os números como faria com qualquer número inteiro. Certifique-se de colocar o quociente sob um novo radical.

Por exemplo,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , assim

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

Imagem intitulada Divide Square Roots Step 4

4. Simplificar, Se necessário. Se o número raiz for um quadrado ou se um dos fatores for um quadrado perfeito, você precisará simplificar a expressão. Um quadrado ou quadrado perfeito é o produto de um inteiro multiplicado por ele mesmo. Por exemplo, 25 é um quadrado perfeito porque

5 \times 5 = 25

$5vezes 5=25$ .

Por exemplo, 4 é um quadrado perfeito porque

2 \times 2 = 4

$2vezes 2=4$ . Por isso:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2vezes 2}}$

= 2

$=2$
assim,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Método 2 de 4: fatoração de raízes

Imagem intitulada Divide Square Roots Step 5

1. Expresse o problema como uma fração. A expressão provavelmente já está escrita desta forma. Se não, altere. Torná-lo uma fração torna as etapas necessárias mais fáceis de seguir, especialmente ao fatorar raízes quadradas. Lembre-se que um caractere de divisão é o mesmo que uma barra de fração.

Por exemplo, ao calcular $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , reescreva a expressão como: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Imagem intitulada Divide Square Roots Step 6

2. Fatore cada cenoura em fatores. Fatore o número como faria com um número inteiro. Deixe os fatores sob os sinais radicais.

Por exemplo:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2times 2times 2}}}{{sqrt{6times 6 }}}}$

Imagem intitulada Divide Square Roots Step 7

3. Simplifique o numerador e o denominador da fração. Para para simplificar uma raiz quadrada, você exclui todos os fatores dos quais o produto é um quadrado?. Um quadrado é o resultado de um número inteiro multiplicado por ele mesmo. O fator agora se torna um coeficiente fora da raiz quadrada.

Por exemplo:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times }}2}}}{{sqrt{{cancel{6times 6}}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
assim,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Imagem intitulada Divide Square Roots Step 8

4. Elimine o sinal de radical do denominador, se necessário. Como regra, uma expressão não pode ter raiz quadrada no denominador. Se sua fração tem raiz quadrada no denominador, você deve eliminá-la. Isso significa remover a raiz no denominador. Para fazer isso, multiplique o numerador e o denominador da fração pela raiz quadrada que você precisa eliminar.

Por exemplo, suponha que sua expressão seja

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , então você tem que multiplicar o numerador e denominador por

\sqrt{3}

${sqrt{3}}$ para remover a raiz quadrada do denominador:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}}times {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Imagem intitulada Divide Square Roots Step 9

5. Simplifique ainda mais, se necessário. Às vezes você fica com coeficientes que podem ser simplificados ainda mais, ou reduzir. Simplifique os inteiros no numerador e no denominador da mesma forma que simplificaria uma fração.

Por exemplo,

\frac{2}{6}

${frac{2}{6}}$ pode ser reduzido a

\frac{1}{3}

${frac{1}{3}}$ , assim

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ pode ser reduzido a

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , ou simplesmente

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Método 3 de 4: Dividindo raízes quadradas com coeficientes

Imagem intitulada Divide Square Roots Step 10

1. Simplifique os coeficientes. Estes são os números fora do radical. Para simplificá-los, compartilhe ou reduzir, ignore as raízes quadradas por enquanto.

Por exemplo, se você $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ tem que calcular, então você simplifica primeiro $\frac{4}{6}$ ${frac{4}{6}}$ . O numerador e o denominador podem ser divididos por um fator de 2. Então você pode simplificar isso para: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Imagem intitulada Divide Square Roots Step 11

2. Simplifique as raízes quadradas. Se o numerador for divisível pelo denominador, basta dividir os números sob os radicais. Caso contrário, simplifique cada raiz quadrada da mesma forma que as outras raízes quadradas.

Por exemplo, como 32 é divisível por 16, você pode dividir as raízes quadradas:

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

Imagem intitulada Divide Square Roots Step 12

3. Multiplique o(s) coeficiente(s) simplificado(s) pela raiz quadrada simplificada. Lembre-se que não pode haver raiz quadrada em um denominador, então ao multiplicar uma fração por uma raiz quadrada, você coloca a raiz quadrada no numerador.

Por exemplo,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Imagem intitulada Divide Square Roots Step 13

4. Elimine a raiz quadrada no denominador, se necessário. Isso é chamado de racionalização do denominador. A regra é que uma expressão não pode ter raiz quadrada no denominador. Para subtrair a raiz do denominador, multiplique o numerador e o denominador pela raiz quadrada que você deseja subtrair.

Por exemplo, se você tiver uma expressão como

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , então você tem que multiplicar o numerador e denominador por

\sqrt{7}

${sqrt{7}}$ para eliminar a raiz quadrada no denominador:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}}times {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Método 4 de 4: Dividindo por um binômio com raiz quadrada

Imagem intitulada Divide Square Roots Step 14

1. Determine se você tem um binômio no denominador. O denominador é o número no problema que você está dividindo por. Um binômio é um polinômio com dois termos. Este método só se aplica à divisão de raízes quadradas envolvendo um binômio.

Por exemplo, se você $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Se você quiser calcular, você tem um binômio no denominador, porque $5 + \sqrt{2}$ $5+{sqrt{2}}$ é um polinômio com dois termos.

Imagem intitulada Divide Square Roots Step 15

2. Determine a conjunção do binômio. Pares conjugados são binômios com os mesmos termos, mas operadores opostos. Usando um par subjuntivo, você pode eliminar a raiz quadrada do denominador.

Por exemplo,

5 + \sqrt{2}

$5+{sqrt{2}}$ e

5 - \sqrt{2}

$5-{sqrt{2}}$ são pares conjuntivos, porque têm os mesmos termos, mas operadores opostos.

Imagem intitulada Divide Square Roots Step 16

3. Multiplique o numerador e o denominador pela conjunção do denominador. Isso permite eliminar a raiz quadrada, pois o produto de um par conjugado é a diferença do quadrado de cada termo no binômio. Aquilo é,

(uma - b) (uma + b) = uma 2 - b^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Por exemplo:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
portanto,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Pontas

Muitas calculadoras têm funções especiais para frações. Insira o coeficiente do numerador, pressione o botão frações e insira o coeficiente do denominador. Quando você pressiona o sinal de igual depois, a calculadora deve reescrever os coeficientes nos menores termos.
Ao contrário da adição e subtração de raízes, em uma fração, as raízes não precisam ser simplificadas primeiro para remover os quadrados. Na verdade, muitas vezes é melhor não fazer isso.
Se você trabalha com raízes quadradas, frações impróprias são mais fáceis de resolver do que números mistos.

Avisos

Nunca coloque um decimal em uma fração. Isso seria de outra forma uma fração dentro de uma fração.
Nunca coloque um número decimal ou misto em uma raiz, converta-o em uma fração e simplifique toda a expressão.
Nunca deixe uma raiz quadrada no denominador de uma fração, mas simplifique a fração.
Se o denominador contiver alguma forma de adição ou subtração, use o método do par conjugado para remover o radical do denominador.