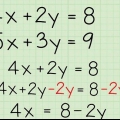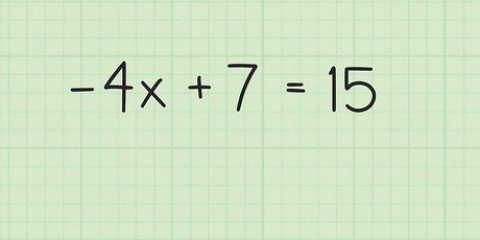Exemplo: nós sabemos isso  e
e  , e assim
, e assim  .
. 
Exemplo:
telefone  em cada lado:
em cada lado: 
Subtraia 3 de cada lado: 
Divida cada lado por 3:  .
.
Exemplo: e
e 



Exemplo: e
e 



Esta é a mesma resposta obtida anteriormente. Nós não cometemos nenhum erro. 
Exemplo: e
e 
As duas linhas se cruzam no ponto (3.6). 
Se as duas linhas são paralelas, elas não se cruzam . Os termos x podem ser eliminados e sua equação pode ser simplificada para uma equação inválida (como  ). Anote aqui`as linhas não se cruzam ou não é uma solução válida` se você responder.
). Anote aqui`as linhas não se cruzam ou não é uma solução válida` se você responder. Se as duas equações descrevem a mesma linha, então elas `se cruzam` em todos os lugares. Você pode eliminar os termos x e simplificar sua equação para uma equação válida (como  ). escreva `as duas linhas são iguais` como resposta.
). escreva `as duas linhas são iguais` como resposta. 

Exemplo: Encontre a interseção de  e
e  .
. Reescreva a equação quadrática em termos de y:  e
e  .
.Este exemplo tem uma equação quadrática e uma equação linear. Problemas com duas equações quadráticas são resolvidos da mesma maneira. 
Exemplo: e
e 


Exemplo:
Subtraia x de cada lado: 
Subtraia 7 de cada lado: 

Exemplo:
O objetivo da fatoração é determinar os dois fatores multiplicados juntos para produzir esta equação. Começando com o primeiro termo, sabemos que  pode ser dividido em x, e x. Escreva (x )(x ) = 0 para mostrar isso.
pode ser dividido em x, e x. Escreva (x )(x ) = 0 para mostrar isso. O último termo é -6. Anote cada par de fatores que se multiplicaram para dar -6 como o produto:  ,
,  ,
,  , e
, e  .
. O termo do meio é x (que você pode escrever como 1x). Some cada par de fatores para obter 1 como resposta. O par certo de fatores é  , Porque
, Porque  .
. Preencha as lacunas em sua resposta com estes poucos fatores:  .
. 
Exemplo (fator): Terminamos com a equação  . Se ambos os fatores entre parênteses são iguais a 0, então a equação é verdadeira. A única solução é
. Se ambos os fatores entre parênteses são iguais a 0, então a equação é verdadeira. A única solução é  →
→  . A outra solução é
. A outra solução é  →
→  .
. Exemplo (equação quadrática ou divisão do quadrado): Se você usar um desses métodos para resolver a equação, uma raiz quadrada aparecerá. Por exemplo, nossa equação se torna  . Lembre-se de que você pode simplificar uma raiz quadrada para duas soluções diferentes:
. Lembre-se de que você pode simplificar uma raiz quadrada para duas soluções diferentes:  , e
, e . Escreva duas equações, uma para cada possibilidade, e resolva x para cada uma delas.
. Escreva duas equações, uma para cada possibilidade, e resolva x para cada uma delas. 
Uma solução: Os problemas podem ser divididos em dois fatores idênticos ((x-1)(x-1) = 0). Introduzido na fórmula quadrática, a raiz quadrada torna-se  . Você só precisa resolver uma equação.
. Você só precisa resolver uma equação. Não há solução real: Não há fatores que atendam aos requisitos (listando para o médio prazo). Entrando na fórmula quadrática você obtém um número negativo sob o radical (como  ). Escreva `sem solução` como sua resposta.
). Escreva `sem solução` como sua resposta. 
Exemplo: Encontramos duas soluções,  e
e  . Uma de nossas linhas tem a equação
. Uma de nossas linhas tem a equação  . substituto
. substituto  e
e  , e resolva cada equação para obter
, e resolva cada equação para obter  e
e  se você receber uma resposta.
se você receber uma resposta. 
Exemplo: Quando nós  entrada, obtemos
entrada, obtemos  , de modo que um ponto de interseção é igual a (2, 9). Fazemos o mesmo para a segunda solução, e isso nos dá o ponto de interseção (-3, 4) sobre.
, de modo que um ponto de interseção é igual a (2, 9). Fazemos o mesmo para a segunda solução, e isso nos dá o ponto de interseção (-3, 4) sobre.
Calcular a intersecção de duas linhas
Contente
Quando linhas retas se cruzam em um gráfico bidimensional, elas o fazem em apenas um ponto, indicado pelas coordenadas x e y. Como ambas as linhas passam por esse ponto, você sabe que as coordenadas x e y devem satisfazer ambas as equações. Com algumas técnicas extras, você pode encontrar as interseções de parábolas e outras curvas quadráticas, usando a mesma lógica.
Degraus
Método 1 de 2: Determinando a interseção entre duas linhas retas

1. Escreva a equação de qualquer linha com y à esquerda. Se necessário, modifique a equação para que y fique isolado em um lado do sinal de igual. Se a equação for escrita com f(x) ou g(x) em vez de y, separe esse termo. Lembre-se que você pode eliminar termos realizando a mesma operação em ambos os lados.
- As equações são desconhecidas, então determine com base nas informações fornecidas.
- Exemplo: Suponha que você tenha duas linhas
e
. Para separar y na segunda equação, adicione 12 a cada lado:

2. Certifique-se de que os lados direitos das equações são iguais. Estamos procurando um ponto onde as duas linhas tenham os mesmos valores xey; este é o ponto onde as linhas se cruzam. Ambas as equações têm apenas um y à esquerda, então sabemos que os lados direitos são iguais entre si. Escreva uma nova equação mostrando isso.
 e
e  , e assim
, e assim  .
.
3. Resolva x na equação. A nova equação tem apenas uma variável, x. Resolva isso com álgebra, realizando a mesma operação em ambos os lados. Encontre os termos x de cada lado da equação e coloque-os na forma x = __ (se não for possível, continue lendo no final desta seção).

 em cada lado:
em cada lado:

 .
.
4. Use este valor de x para resolver para y. Escolha a equação de cada linha. Substitua cada x na equação pela resposta que você encontrou. Agora resolva para y.
 e
e 



5. Verifique seu trabalho. É aconselhável inserir seu valor x na outra equação para ver se você obtém o mesmo resultado. Se você obtiver outra solução para y, volte e verifique se há erros no seu trabalho.
 e
e 




6. Anote as coordenadas x e y da interseção. Agora você resolveu o valor x e o valor y da interseção das duas linhas. Escreva o ponto como uma coordenada, com o valor x como o primeiro número.
 e
e 

7. Processe resultados incomuns. Algumas equações tornam impossível resolver x. Isso não significa necessariamente que você cometeu um erro. Existem duas maneiras pelas quais um par de linhas pode levar a uma solução especial:
 ). Anote aqui`as linhas não se cruzam ou não é uma solução válida` se você responder.
). Anote aqui`as linhas não se cruzam ou não é uma solução válida` se você responder. ). escreva `as duas linhas são iguais` como resposta.
). escreva `as duas linhas são iguais` como resposta.Método 2 de 2: Problemas com equações do segundo grau

1. Aprenda a reconhecer equações do segundo grau. Em uma equação quadrática, há uma ou mais variáveis na forma quadrática ( ou
ou  ), e não há poderes superiores. As linhas representadas pelas equações são curvas e podem, portanto, cruzar uma linha reta em 0, 1 ou 2 pontos. Nesta parte você aprenderá como encontrar as interseções de tal problema.
), e não há poderes superiores. As linhas representadas pelas equações são curvas e podem, portanto, cruzar uma linha reta em 0, 1 ou 2 pontos. Nesta parte você aprenderá como encontrar as interseções de tal problema.
 ou
ou  ), e não há poderes superiores. As linhas representadas pelas equações são curvas e podem, portanto, cruzar uma linha reta em 0, 1 ou 2 pontos. Nesta parte você aprenderá como encontrar as interseções de tal problema.
), e não há poderes superiores. As linhas representadas pelas equações são curvas e podem, portanto, cruzar uma linha reta em 0, 1 ou 2 pontos. Nesta parte você aprenderá como encontrar as interseções de tal problema. - Trabalhe as equações entre parênteses para ver se elas são quadráticas. Por exemplo,
é quadrático, porque você pode colocá-lo fora dos parênteses se
- Ter equações de um círculo ou uma elipse Ambas uma
como um
prazo. Se você achar esses casos especiais difíceis, continue lendo Dicas no final deste artigo.

2. Escreva as equações em termos de y. Se necessário, reescreva cada equação de modo que y fique de um lado.
 e
e  .
. e
e  .
.
3. Combine as duas equações para eliminar o y. Se você fez ambas as equações iguais a y, então você sabe que as duas equações sem o y são iguais entre si.
 e
e 


4. Reorganize a nova equação para que um lado seja igual a zero. Use métodos matemáticos padrão para obter todos os termos em um lado da equação. Esta é a configuração necessária dos problemas para poder resolvê-los na próxima etapa.




5.Resolva a equação quadrática. Se você tem um lado igual a zero, existem três maneiras de resolver a equação quadrática. Todo mundo prefere um método diferente. Você pode ler mais sobre a fórmula quadrática de `dividir o quadrado`, ou você pode seguir este exemplo ainda mais para ele fatorar método:

 pode ser dividido em x, e x. Escreva (x )(x ) = 0 para mostrar isso.
pode ser dividido em x, e x. Escreva (x )(x ) = 0 para mostrar isso. ,
,  ,
,  , e
, e  .
. , Porque
, Porque  .
. .
.
6. Mantenha os olhos abertos para duas soluções para x. Se você trabalhar muito rápido, poderá encontrar uma resposta para o problema sem perceber que existe outra. Veja como encontrar os dois valores de x para linhas que se cruzam em dois pontos:
 . Se ambos os fatores entre parênteses são iguais a 0, então a equação é verdadeira. A única solução é
. Se ambos os fatores entre parênteses são iguais a 0, então a equação é verdadeira. A única solução é  →
→  . A outra solução é
. A outra solução é  →
→  .
. . Lembre-se de que você pode simplificar uma raiz quadrada para duas soluções diferentes:
. Lembre-se de que você pode simplificar uma raiz quadrada para duas soluções diferentes:  , e
, e . Escreva duas equações, uma para cada possibilidade, e resolva x para cada uma delas.
. Escreva duas equações, uma para cada possibilidade, e resolva x para cada uma delas.
7. Resolver problemas com uma ou zero soluções. Duas linhas que mal se tocam têm uma interseção, e duas linhas que nunca se tocam têm zero. Você pode reconhecê-los das seguintes maneiras:
 . Você só precisa resolver uma equação.
. Você só precisa resolver uma equação. ). Escreva `sem solução` como sua resposta.
). Escreva `sem solução` como sua resposta.
8. Conecte os valores x de volta à equação original. Uma vez que você tenha o valor x da interseção, coloque-o de volta em uma das equações com as quais você começou. Resolva para y para encontrar o valor de y. Se houver um segundo valor x, repita para este valor também.
 e
e  . Uma de nossas linhas tem a equação
. Uma de nossas linhas tem a equação  . substituto
. substituto  e
e  , e resolva cada equação para obter
, e resolva cada equação para obter  e
e  se você receber uma resposta.
se você receber uma resposta.
9. Escreva a resposta como coordenadas. Agora você escreve a resposta como coordenadas, com o valor x e o valor y da interseção. Se você tiver duas respostas, certifique-se de combinar o valor x correto com cada valor y.
 entrada, obtemos
entrada, obtemos  , de modo que um ponto de interseção é igual a (2, 9). Fazemos o mesmo para a segunda solução, e isso nos dá o ponto de interseção (-3, 4) sobre.
, de modo que um ponto de interseção é igual a (2, 9). Fazemos o mesmo para a segunda solução, e isso nos dá o ponto de interseção (-3, 4) sobre.Pontas
- As equações para um círculo ou elipse têm um
prazo e uma
prazo. Para encontrar a interseção de um círculo e uma linha reta, resolva x dentro da equação linear. Substitua a solução de x na equação do círculo, e a equação quadrática ficou muito mais fácil. Esses problemas podem ter 0, 1 ou 2 soluções, conforme já indicado nos métodos acima.
- Um círculo e uma parábola (ou qualquer outra equação quadrática) podem ter 0, 1, 2, 3 ou 4 soluções. Encontre a variável que é um quadrado em ambas as equações - digamos que isso é x. solto
e substitua a resposta por
na outra equação. Resolva y para encontrar as soluções 0, 1 ou 2. Conecte cada solução de volta à equação quadrática original e resolva para x. Cada um deles pode ter 0, 1 ou 2 soluções.
Artigos sobre o tópico "Calcular a intersecção de duas linhas"
Оцените, пожалуйста статью
Popular