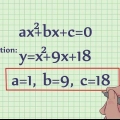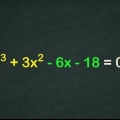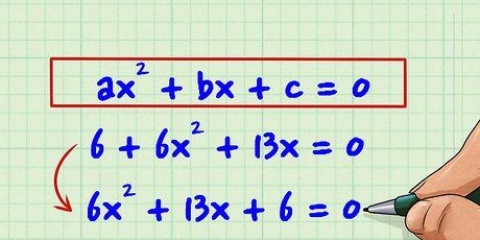Em álgebra, uma equação quadrática é um polinômio que consiste em 3 termos, da forma ax + bx + c. Polinômios têm muitas aplicações em matemática e ciências, e resolver equações quadráticas é uma habilidade importante. Enquanto a maioria das equações quadráticas podem ser simplesmente fatoradas, existem vários casos em que uma equação quadrática deve ser fatorada de uma maneira especial.Se nenhum dos métodos no guia a seguir for útil, pode ser necessário usar métodos para fatorar polinômios mais altos.
Degraus
Método 1 de 4: Divisão Dois
1. Ordene os argumentos da equação quadrática do maior para o menor. Um argumento é uma variável no polinômio; a ordem normal de colocação dos termos é da maior potência para a menor. Então, 5 + x + 6x deve ser ordenado como x + 6x + 5.
2. Excluir todos os fatores que ocorrem em todos os três termos. Se as constantes da equação quadrática forem todas múltiplas do mesmo número, você poderá colocá-las fora dos parênteses, ou se cada componente da equação quadrática tiver uma variável igual, essa variável poderá ser colocada fora dos colchetes.
Por exemplo, na equação quadrática -8a + 24a + 144, cada constante é um múltiplo de 8, então 8 pode ser colocado fora dos parênteses, dando -8(a - 3a - 18). Mesmo que o coeficiente -3 e a constante -18 sejam divisíveis por -3, o coeficiente 1 do primeiro termo não é, então não podemos fatorar mais.Na equação quadrática - x - 2x - 1, cada termo é divisível por -1, que após fatoração pode ser escrito como (-1)(x + 2x + 1).3. Procure padrões que facilitem a resolução de uma equação quadrática. Para obter informações e exemplos cada vez mais detalhados, consulte o método para resolver casos especiais de uma equação quadrática.
4. Se possível, tente dividir a equação quadrática em 2 dois termos da forma (mx + n)(qx + r). Isso geralmente é apenas tentar o que funciona, mas existem truques que tornam isso mais fácil. Vamos primeiro supor que o primeiro termo na equação quadrática (o termo x) é igual a 1 (o termo se parece mais com x do que, por exemplo,., 3x). Os valores m e q dos dois termos são 1, então sua solução ficará como (x + b)(x + d). Em seguida, encontre para sua equação da forma ax + bx + c, os valores n e r tais que: n * r = c e n + r = b.
No exemplo, x + 6x + 5, 5 * 1 = 5 e 5 + 1 = 6. Então, a solução é (x + 1)(x + 5).Se nem todos os termos da equação quadrática forem positivos, não se esqueça de considerar os números negativos. Por exemplo, x - 3x - 18 fator em (x - 6)(x + 3) porque -6 + 3 = -3 e -6 * 3 = -18.5. Se a constante no primeiro termo não for igual a 1 (por exemplo,. se parecer mais com 3x do que com x), a fatoração se torna um pouco mais difícil e, via ax + bx + c, você finalmente obtém uma solução na forma (mx + n) (qx + r). Para uma solução correta, m * q = a, m * r + n * q = b, e n * r = c.
Comece fazendo uma lista de todos os fatores possíveis de a e c. Em seguida, verifique qual par de fatores funciona, usando as restrições indicadas acima.Por exemplo, pegue 3x + 10x + 8. Os pares de fatores possíveis de 3 são 1 * 3. Os pares de fatores possíveis de 8 são 1 * 8 e 2 * 4. Como 3 * 1 = 3 (o termo da equação quadrática), 1 * 4 + 2 * 3 = 10 (o termo b) e 2 * 4 = 8 (o termo c), a solução é (3x + 4) (x + 2).Método 2 de 4: Fatorando casos especiais
1. Verifique se a constante no primeiro termo ou no terceiro termo da equação é primo. Um número primo só é divisível por ele mesmo e por 1. Isso diminui o número de possíveis fatores binomiais. No exemplo anterior: x + 6x + 5 existe apenas 1 conjunto possível de fatores binomiais, (x + 5)(x + 1), pois 5 é primo.
2. Verifique se a equação quadrática é um quadrado perfeito. Isso requer que os valores dos coeficientes a e c da equação ax + bx + c sejam quadrados perfeitos (e positivos!), e que o valor de b é o dobro do valor do produto da raiz quadrada de a e c.
(x + a) torna-se x + 2ax + a. Por exemplo, (x + 3) = x + 6x + 9 e (3x + 2) = 9x + 12x + 4.Da mesma forma, (x - a) torna-se x - 2ax + a. Por exemplo, (x - 3) = x - 6x + 9.3. Para algumas equações quadráticas da forma x - n:
(x + a)(x - a) torna-se x - a. Então x - 9 pode ser rapidamente fatorado em (x + 3)(x - 3), e 4x - 4 = (2x + 2)(2x - 2).Método 3 de 4: Usando a fórmula abc
Para equações quadráticas da forma ax + bx + c que são difíceis ou impossíveis de resolver, use a fórmula abc.
1. Aprenda a usar a fórmula abc.
2. Digite a, b e c e resolva a primeira parte da fórmula. Suponha que temos a equação quadrática x + 5x + 6.
Comece com b - 4ac, que é 5 - 4(1)(6) = 1. A raiz quadrada de 1 é 1.Termine resolvendo a equação. -b + 1 = -5 + 1 = -4. Divida isso por 2a (2 * 1 = 2) para obter -2 como resposta.3. Resolva a outra parte. Já sabemos que a raiz quadrada de b - 4ac = 1. -b - 1 = -6. Divida isso por 2a (2) para obter -3.
4. Verifique suas soluções preenchendo-as para x. Às vezes, uma ou mais das respostas não são soluções válidas (por exemplo, se forem números imaginários). Mas se uma equação quadrática tem uma solução, então a equação irá encontrá-la.
Note que se tivéssemos fatorado esta equação, ao invés de usar a fórmula abc, teríamos como resposta (x + 2)(x + 3). Se você definir essa equação igual a 0, obterá duas soluções, x = 2 e x = -3, que também encontramos com a fórmula.Método 4 de 4: O quadrado oculto em um polinômio
Algumas equações quadráticas são de ordem superior, mas essencialmente apenas quadráticas. Uma vez reconhecido como tal, você pode tratá-los como tal usando a substituição.
1.
Veja as variáveis em cada termo.Por exemplo, x - 7x + 12 parece ser uma potência de 6, mas após a substituição de u = x, isso se torna u - 7u + 12. Isso deixa você com uma equação que é muito mais fácil de resolver.
- Substituições mais complexas podem ajudar a resolver problemas mais complicados. Por exemplo, xy - 7xy + 12y é simplificado para xy(u - 7u + 12) e após a substituição u = x/y. Tal substituição é possível sempre que a soma das potências dos dois termos for duas vezes a potência do termo restante.
2. Se tal substituição puder ocorrer, então fatore o polinômio simples, neste caso, u - 7u + 12 = (u-3)(u-4)
3. Desfaça a substituição e aplique x à solução. Então, substitua u por x , x - 7x + 12 = (x - 3)(x - 4). Se possível ou desejado, cada fator pode ser simplificado ainda mais.
Pontas
- Use o critério de Eisenstein para determinar rapidamente se um polinômio é não redutível e não fatorável. Este critério se aplica a qualquer polinômio, mas especialmente a uma equação quadrática. Se houver um número primo p que torna os dois últimos termos divisíveis e satisfaz as seguintes condições, então o polinômio não pode ser reduzido:
- O termo constante (o c em uma equação quadrática da forma ax + bx + c) é um plural de p, mas não de p.
- O primeiro termo (aqui, a) não é plural de p.
- Por exemplo, 14x + 45x + 51 é irredutível porque tem um número primo (3) que torna 45 e 51 divisíveis, mas não 14 e 51, que não são divisíveis por 3.
Você pode fatorar polinômios de múltiplas variáveis usando os métodos acima se forem equações quadráticas assumindo alguma variável. Por exemplo, pegue 4xy - 5x + 15y. Isso pode ser reescrito como (4x)y + 15y - 5x. Observe que isso se encaixa na forma ax + bx + c, onde a = 4x e c = 5x. Esta equação pode então ser resolvida com a fórmula abc.Você pode praticar a fatoração de equações quadráticas resolvendo problemas em um livro que trata de álgebra.Avisos
- Embora verdadeiro para quadrados, equações quadráticas que podem ser fatoradas não são necessariamente o produto de dois binários. Um contra-exemplo é x + 105x + 46 = (x + 5x + 2)(x - 5x + 23).
Necessidades
- Livro de álgebra/matemática
- Papel e lápis
Artigos sobre o tópico "Fatorar"