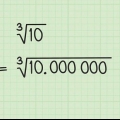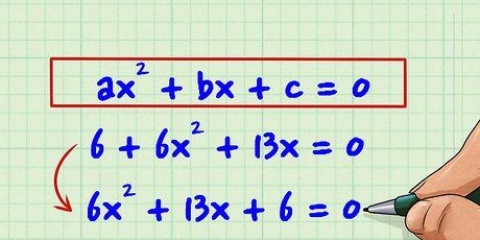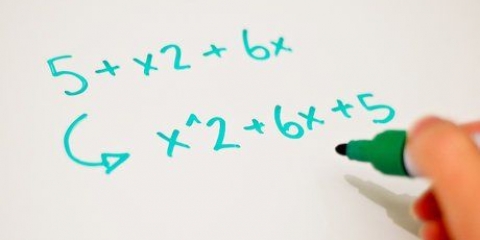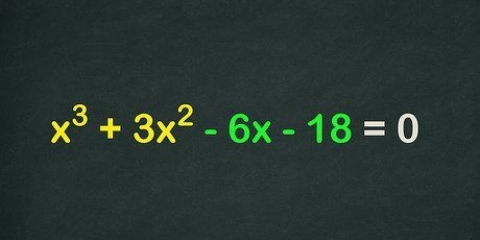→
→ 
 →
→ 
 →
→ 
Observe como os sinais de menos permanecem na frente do 2. Quando um termo é subtraído, o sinal de menos permanece na frente dele. 
Atribuição do exercício: .
. Fatores de 3:1, 3 Fatores de 6: 1, 2, 3, 6. `O máximo divisor comum é 3`. 
Atribuição do exercício: .
. Encontre os máximos divisores comuns: 3 Para remover o fator de ambos os termos:

Atribuição do exercício:
Encontre os máximos divisores comuns: 3 Para remover o fator de ambos os termos:
Multiplique o fator pela nova expressão:
Resposta final dissolvida: 

Para reordenar os termos:
Encontrando o máximo divisor comum:
Para remover o fator de ambos os termos:
Multiplique o fator pela nova expressão:
Verifique a resposta:


Atribuição do exercício:
igual a zero:


Atribuição do exercício:
igual a zero:
Dissolver:

Atribuição do exercício:
igual a zero:
Dissolver:
Faça ambos os termos iguais a zero 0: 




y = 0 

y = 4 


 Esta resposta está correta
Esta resposta está correta

 Essa resposta também está correta.
Essa resposta também está correta.

Atribuição original:
Para reordenar os termos:
Para mesclar termos semelhantes:
Encontre os máximos divisores comuns:
Dissolver:

A fórmula para a diferença de quadrados perfeitos:
Atribuição do exercício:
Determine as raízes quadradas: 

Aplique raízes quadradas à fórmula: 

Fórmula da diferença de terceiras potências:
Atribuição do exercício:
Determine as raízes cúbicas: ![Binômios de fatoração {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômios de fatoração {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Aplique cubos à fórmula: 

Fórmula da soma de cubos perfeitos:
Atribuição do exercício:
Determine as raízes cúbicas: ![Binômios de fatoração {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômios de fatoração {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Aplique os cubos à fórmula: 
Binômios de fatoração
Contente
Em álgebra, binômios são expressões de dois termos conectadas por um sinal de mais ou menos, como 
Degraus
Parte 1 de 3: Binomiais de fatoração

1. Revise os conceitos básicos de fatoração novamente. Fatorar é dividir um número grande em seus divisores mais simples. Cada uma dessas partes é chamada de `fator`. Por exemplo, o número 6 é divisível por quatro números diferentes: 1, 2, 3 e 6. Então 1, 2, 3 e 6 são os fatores de 6.
- Os fatores de 32 são 1, 2, 4, 8, 16 e 32
- Tanto `1` quanto o número que você fatora são sempre fatores. Então os fatores de um número pequeno como 3 são apenas 1 e 3.
- Fatores são apenas aqueles números que são totalmente divisíveis, ou seja, os números `inteiros`. Você pode dividir 32 por 3,564 ou 21,4952, mas esses não são fatores, apenas números decimais.

2. Liste os termos do binômio para torná-los mais fáceis de ler. Um binômio nada mais é do que a adição ou subtração de dois termos, pelo menos um dos quais contém uma variável. Às vezes, essas variáveis têm expoentes, como  ou
ou  . Se você está tentando fatorar binômios pela primeira vez, ajuda ordenar as equações em termos de variáveis decrescentes, o que significa que o maior expoente vem por último. Por exemplo:
. Se você está tentando fatorar binômios pela primeira vez, ajuda ordenar as equações em termos de variáveis decrescentes, o que significa que o maior expoente vem por último. Por exemplo:
 ou
ou  . Se você está tentando fatorar binômios pela primeira vez, ajuda ordenar as equações em termos de variáveis decrescentes, o que significa que o maior expoente vem por último. Por exemplo:
. Se você está tentando fatorar binômios pela primeira vez, ajuda ordenar as equações em termos de variáveis decrescentes, o que significa que o maior expoente vem por último. Por exemplo: →
→ 
 →
→ 
 →
→ 

3. Encontre o máximo divisor comum dos dois termos. Isso significa que você está procurando o maior número que ambas as partes do binômio são divisíveis por. Se isso não funcionar, fatore os dois números por conta própria e veja qual é o número correspondente mais alto. Por exemplo:
 .
.
4. Divida o máximo divisor comum para cada termo. Se você conhece o denominador comum, deve removê-lo de cada termo. Observe que você acabou de dividir os termos, tornando cada um deles um problema de divisão menor. Se feito corretamente, ambas as equações têm o mesmo fator:
 .
.

5. Multiplique seu fator pela expressão resultante para arredondar. No último problema, você removeu um 3 e obtém  . Mas você não quer se livrar dos 3 completamente, apenas os leve em consideração para simplificar as coisas. Você não pode simplesmente excluir números sem colocá-los de volta! Multiplique o fator pela expressão para completar esta seção. Por exemplo:
. Mas você não quer se livrar dos 3 completamente, apenas os leve em consideração para simplificar as coisas. Você não pode simplesmente excluir números sem colocá-los de volta! Multiplique o fator pela expressão para completar esta seção. Por exemplo:
 . Mas você não quer se livrar dos 3 completamente, apenas os leve em consideração para simplificar as coisas. Você não pode simplesmente excluir números sem colocá-los de volta! Multiplique o fator pela expressão para completar esta seção. Por exemplo:
. Mas você não quer se livrar dos 3 completamente, apenas os leve em consideração para simplificar as coisas. Você não pode simplesmente excluir números sem colocá-los de volta! Multiplique o fator pela expressão para completar esta seção. Por exemplo:




6. Verifique seu trabalho multiplicando para a equação original. Se você fez tudo certo, é fácil verificar se fez certo. Multiplique seu fator por ambos os termos individuais entre parênteses. Se corresponder ao binômio original, você fez tudo certo. Do início ao fim resolvemos a expressão  para praticar:
para praticar:
 para praticar:
para praticar:




Parte 2 de 3: Fatorando binômios para resolver equações

1. Fator para simplificar equações para que sejam mais fáceis de resolver. Ao resolver uma equação com binômios, especialmente binômios complexos, pode parecer que não há como fazer tudo corresponder. Por exemplo, tente resolver o seguinte:  . Uma maneira de fazer isso, especialmente com expoentes, é fatorar primeiro.
. Uma maneira de fazer isso, especialmente com expoentes, é fatorar primeiro.
 . Uma maneira de fazer isso, especialmente com expoentes, é fatorar primeiro.
. Uma maneira de fazer isso, especialmente com expoentes, é fatorar primeiro. - Atribuição do exercício:
- Lembre-se que binômios só podem ter dois termos. Se houver mais de dois termos, você deve Aprenda a resolver polinômios.

2. Adicionar e subtrair para que um lado da equação seja igual a zero. Toda essa estratégia se baseia em um dos fatos mais fundamentais da matemática: algo multiplicado por zero deve ser igual a zero. Então, se sua equação é igual a zero, então um dos termos fatorados deve ser igual a zero! Para começar, você irá adicionar e subtrair para que um lado seja igual a zero.




3. Dissolva o lado diferente de zero como você está acostumado. Neste ponto você está apenas fingindo que o outro lado não existe. Encontre o máximo divisor comum, divida-o e crie sua expressão fatorada.




4. Defina os termos dentro e fora dos parênteses iguais a zero. No problema prático você multiplica 2y por (4 – y), e isso deve ser igual a zero. Como algo multiplicado por zero é igual a zero, isso significa que 2y ou (4 – y) deve ser igual a zero. Faça duas equações separadas para descobrir qual valor y deve ter para tornar cada lado igual a zero.






5. Resolva ambas as equações para zero para a resposta ou respostas finais. Você pode obter uma resposta ou várias respostas. Lembre-se, apenas um lado deve ser igual a zero, para que você possa obter alguns valores diferentes para y que resolvam a mesma equação. Os últimos passos da atribuição do exercício:





6. Aplique suas respostas de volta à equação original para se certificar de que estão corretas. Depois de encontrar os valores corretos para y, você poderá usá-los para resolver a equação. Isso é tão simples quanto experimentar cada valor de y em vez da variável como mostrado abaixo. As respostas são y = 0 e y = 4, então:


 Esta resposta está correta
Esta resposta está correta

 Essa resposta também está correta.
Essa resposta também está correta.Parte 3 de 3: Lidando com problemas mais difíceis

1. Lembre-se que as variáveis contam como fatores, mesmo com expoentes. Lembre-se de que fatorar é determinar quais números se encaixam no inteiro. A expressão  é outra maneira de dizer
é outra maneira de dizer  . Isso significa que você pode colocar qualquer x fora dos parênteses se o outro termo também tiver um. Trate variáveis como números regulares. Por exemplo:
. Isso significa que você pode colocar qualquer x fora dos parênteses se o outro termo também tiver um. Trate variáveis como números regulares. Por exemplo:
 é outra maneira de dizer
é outra maneira de dizer  . Isso significa que você pode colocar qualquer x fora dos parênteses se o outro termo também tiver um. Trate variáveis como números regulares. Por exemplo:
. Isso significa que você pode colocar qualquer x fora dos parênteses se o outro termo também tiver um. Trate variáveis como números regulares. Por exemplo: pode ser fatorado, porque ambos os termos contêm um t. A resposta final será
- Você pode até colocar várias variáveis fora dos parênteses ao mesmo tempo. Por exemplo, em
ambos os termos contêm o mesmo
. Você pode dissolver isso em

2. Reconhecer binômios ainda não simplificados combinando termos semelhantes. Tomemos, por exemplo, a expressão  . Aqui parece que você está lidando com quatro termos, mas se você olhar mais de perto, perceberá que existem apenas dois. Você pode adicionar termos semelhantes e, como 6 e 14 não têm variável e 2x e 3x compartilham a mesma variável, eles podem ser mesclados. Dissolver é então fácil:
. Aqui parece que você está lidando com quatro termos, mas se você olhar mais de perto, perceberá que existem apenas dois. Você pode adicionar termos semelhantes e, como 6 e 14 não têm variável e 2x e 3x compartilham a mesma variável, eles podem ser mesclados. Dissolver é então fácil:
 . Aqui parece que você está lidando com quatro termos, mas se você olhar mais de perto, perceberá que existem apenas dois. Você pode adicionar termos semelhantes e, como 6 e 14 não têm variável e 2x e 3x compartilham a mesma variável, eles podem ser mesclados. Dissolver é então fácil:
. Aqui parece que você está lidando com quatro termos, mas se você olhar mais de perto, perceberá que existem apenas dois. Você pode adicionar termos semelhantes e, como 6 e 14 não têm variável e 2x e 3x compartilham a mesma variável, eles podem ser mesclados. Dissolver é então fácil:





3. Reconhecer a especial `diferença de quadrados perfeitos`. Um quadrado perfeito é um número cuja raiz é um número inteiro, como 
 ,
, 
 , ou mesmo
, ou mesmo 
 Se o seu binômio é uma soma negativa com dois quadrados perfeitos, como
Se o seu binômio é uma soma negativa com dois quadrados perfeitos, como  , então você pode simplesmente usá-los nesta fórmula:
, então você pode simplesmente usá-los nesta fórmula:

 ,
, 
 , ou mesmo
, ou mesmo 
 Se o seu binômio é uma soma negativa com dois quadrados perfeitos, como
Se o seu binômio é uma soma negativa com dois quadrados perfeitos, como  , então você pode simplesmente usá-los nesta fórmula:
, então você pode simplesmente usá-los nesta fórmula:





4. Aprenda a simplificar a `diferença de cubos perfeitos`. Como os quadrados perfeitos, esta é uma fórmula simples onde dois cubos são subtraídos um do outro. Por exemplo,  . Como antes, encontre a raiz cúbica de cada um e use isso na fórmula:
. Como antes, encontre a raiz cúbica de cada um e use isso na fórmula:
 . Como antes, encontre a raiz cúbica de cada um e use isso na fórmula:
. Como antes, encontre a raiz cúbica de cada um e use isso na fórmula:

![Binômios de fatoração {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômios de fatoração {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Saiba que a soma de cubos perfeitos também se encaixa em uma fórmula. Ao contrário da diferença de quadrados perfeitos, você pode usar cubos adicionados, como  , também fácil de encontrar com uma fórmula simples. Isso é quase exatamente o mesmo que acima, mas com alguns prós e contras invertidos. A fórmula é tão fácil quanto as outras duas, e tudo o que você precisa fazer é reconhecer os dois cubos do problema:
, também fácil de encontrar com uma fórmula simples. Isso é quase exatamente o mesmo que acima, mas com alguns prós e contras invertidos. A fórmula é tão fácil quanto as outras duas, e tudo o que você precisa fazer é reconhecer os dois cubos do problema:
 , também fácil de encontrar com uma fórmula simples. Isso é quase exatamente o mesmo que acima, mas com alguns prós e contras invertidos. A fórmula é tão fácil quanto as outras duas, e tudo o que você precisa fazer é reconhecer os dois cubos do problema:
, também fácil de encontrar com uma fórmula simples. Isso é quase exatamente o mesmo que acima, mas com alguns prós e contras invertidos. A fórmula é tão fácil quanto as outras duas, e tudo o que você precisa fazer é reconhecer os dois cubos do problema:

![Binômios de fatoração {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binômios de fatoração {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Pontas
- Nem todos os binômios têm divisores comuns! Alguns já foram simplificados o máximo possível.
- Se você não tem certeza se existe um divisor comum, divida por números menores primeiro. Por exemplo, se você não ver imediatamente que 16 é o divisor comum de 32 e 16, comece a dividir os dois números por 2. Isso deixa 16 e 8, que também podem ser divididos por 8. Agora você tem 2 e 1, os menores fatores. Há claramente um divisor comum maior que 8 e 2.
- Observe que uma sexta potência (x) é um quadrado perfeito e é um cubo perfeito. Portanto, você pode aplicar qualquer fórmula especial acima, em qualquer ordem, a um binômio que é a diferença de sextas potências perfeitas, como x - 64. No entanto, você pode achar mais fácil aplicar a fórmula de diferença para quadrados perfeitos primeiro para que você possa fatorar ainda mais o binômio.
Avisos
- Um binômio que é a soma de quadrados perfeitos não pode ser fatorado.
Artigos sobre o tópico "Binômios de fatoração"
Оцените, пожалуйста статью
Popular