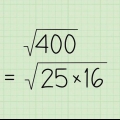Fica claro aqui porque  , Porque
, Porque  está no denominador e você não pode dividir por zero.
está no denominador e você não pode dividir por zero. Se precisar, você pode estender o lado esquerdo para garantir que a esquadria funcione. 

Agora podemos nos livrar dos sinais de valor absoluto, por  colocar à direita. Podemos fazer isso porque o valor absoluto não distingue entre números positivos e negativos, então ambos são válidos. Este detalhe é porque a equação quadrática torna possível obter duas raízes como resultado.
colocar à direita. Podemos fazer isso porque o valor absoluto não distingue entre números positivos e negativos, então ambos são válidos. Este detalhe é porque a equação quadrática torna possível obter duas raízes como resultado. 
Vamos simplificar um pouco mais essa expressão. Como a raiz quadrada de um quociente é o quociente das raízes quadradas, podemos escrever o lado direito como  Então podemos tirar a raiz quadrada do denominador.
Então podemos tirar a raiz quadrada do denominador. 


Aprenda divisão quadrada
Uma das habilidades mais importantes para estudantes de matemática é a fórmula abc, ou 


Degraus
1. Comece com a forma padrão de uma equação quadrática geral. Embora qualquer comparação com um termo como  in, é quadrático, a forma padrão define tudo para zero. Lembre-se disso
in, é quadrático, a forma padrão define tudo para zero. Lembre-se disso  são coeficientes que podem ser qualquer número inteiro, então agora você não pode preencher números para as variáveis - queremos trabalhar com a forma geral.
são coeficientes que podem ser qualquer número inteiro, então agora você não pode preencher números para as variáveis - queremos trabalhar com a forma geral.
 in, é quadrático, a forma padrão define tudo para zero. Lembre-se disso
in, é quadrático, a forma padrão define tudo para zero. Lembre-se disso  são coeficientes que podem ser qualquer número inteiro, então agora você não pode preencher números para as variáveis - queremos trabalhar com a forma geral.
são coeficientes que podem ser qualquer número inteiro, então agora você não pode preencher números para as variáveis - queremos trabalhar com a forma geral. - A única condição é que
, caso contrário, a equação é simplificada para uma equação linear. Veja se você pode encontrar soluções gerais para casos especiais onde
e
.
2. puxar c  fora de ambos os lados. Nosso objetivo é isolar
fora de ambos os lados. Nosso objetivo é isolar  . Começamos movendo um dos coeficientes para o outro lado, de modo que o lado esquerdo consista apenas em termos com
. Começamos movendo um dos coeficientes para o outro lado, de modo que o lado esquerdo consista apenas em termos com  .
.
 fora de ambos os lados. Nosso objetivo é isolar
fora de ambos os lados. Nosso objetivo é isolar  . Começamos movendo um dos coeficientes para o outro lado, de modo que o lado esquerdo consista apenas em termos com
. Começamos movendo um dos coeficientes para o outro lado, de modo que o lado esquerdo consista apenas em termos com  .
.
3. Divida os dois lados uma  . Observe que poderíamos ter trocado isso na etapa anterior e ainda obter a mesma resposta. Lembre-se de que dividir um polinômio por algo envolve dividir cada um de seus termos individuais. Isso facilita a divisão do quadrado.
. Observe que poderíamos ter trocado isso na etapa anterior e ainda obter a mesma resposta. Lembre-se de que dividir um polinômio por algo envolve dividir cada um de seus termos individuais. Isso facilita a divisão do quadrado.
 . Observe que poderíamos ter trocado isso na etapa anterior e ainda obter a mesma resposta. Lembre-se de que dividir um polinômio por algo envolve dividir cada um de seus termos individuais. Isso facilita a divisão do quadrado.
. Observe que poderíamos ter trocado isso na etapa anterior e ainda obter a mesma resposta. Lembre-se de que dividir um polinômio por algo envolve dividir cada um de seus termos individuais. Isso facilita a divisão do quadrado.
4.Divida o quadrado. Lembre-se que o objetivo é criar uma expressão  reescrever como
reescrever como  através do qual
através do qual  é um coeficiente. Isso pode não ser imediatamente claro para você. Para ficar mais claro, reescreva
é um coeficiente. Isso pode não ser imediatamente claro para você. Para ficar mais claro, reescreva  E se
E se  multiplicando o termo por
multiplicando o termo por  Podemos fazer isso porque multiplicar por 1 não muda nada. Agora podemos ver claramente em nosso caso que
Podemos fazer isso porque multiplicar por 1 não muda nada. Agora podemos ver claramente em nosso caso que  , então só falta o termo
, então só falta o termo  . Assim, para dividir o quadrado, adicionamos em ambos os lados - ou seja,,
. Assim, para dividir o quadrado, adicionamos em ambos os lados - ou seja,,  E então é claro que podemos fatorar.
E então é claro que podemos fatorar.
 reescrever como
reescrever como  através do qual
através do qual  é um coeficiente. Isso pode não ser imediatamente claro para você. Para ficar mais claro, reescreva
é um coeficiente. Isso pode não ser imediatamente claro para você. Para ficar mais claro, reescreva  E se
E se  multiplicando o termo por
multiplicando o termo por  Podemos fazer isso porque multiplicar por 1 não muda nada. Agora podemos ver claramente em nosso caso que
Podemos fazer isso porque multiplicar por 1 não muda nada. Agora podemos ver claramente em nosso caso que  , então só falta o termo
, então só falta o termo  . Assim, para dividir o quadrado, adicionamos em ambos os lados - ou seja,,
. Assim, para dividir o quadrado, adicionamos em ambos os lados - ou seja,,  E então é claro que podemos fatorar.
E então é claro que podemos fatorar.
 , Porque
, Porque  está no denominador e você não pode dividir por zero.
está no denominador e você não pode dividir por zero.5. Escreva o lado direito sob um denominador comum. Queremos que ambos os denominadores sejam  são, então multiplique o termo
são, então multiplique o termo  de
de  .
.
 são, então multiplique o termo
são, então multiplique o termo  de
de  .
.
6. Calcule a raiz quadrada de ambos os lados. No entanto, é essencial que você entenda que, ao fazer isso, você está essencialmente dando dois passos. Quando você tira a raiz quadrada de  , então você consegue
, então você consegue  não. Você basicamente obtém o valor absoluto disso,
não. Você basicamente obtém o valor absoluto disso,  . Este valor absoluto é essencial para obter ambas as raízes - simplesmente colocar raízes quadradas acima de ambos os lados produzirá apenas uma das raízes.
. Este valor absoluto é essencial para obter ambas as raízes - simplesmente colocar raízes quadradas acima de ambos os lados produzirá apenas uma das raízes.
 , então você consegue
, então você consegue  não. Você basicamente obtém o valor absoluto disso,
não. Você basicamente obtém o valor absoluto disso,  . Este valor absoluto é essencial para obter ambas as raízes - simplesmente colocar raízes quadradas acima de ambos os lados produzirá apenas uma das raízes.
. Este valor absoluto é essencial para obter ambas as raízes - simplesmente colocar raízes quadradas acima de ambos os lados produzirá apenas uma das raízes.
 colocar à direita. Podemos fazer isso porque o valor absoluto não distingue entre números positivos e negativos, então ambos são válidos. Este detalhe é porque a equação quadrática torna possível obter duas raízes como resultado.
colocar à direita. Podemos fazer isso porque o valor absoluto não distingue entre números positivos e negativos, então ambos são válidos. Este detalhe é porque a equação quadrática torna possível obter duas raízes como resultado.
 Então podemos tirar a raiz quadrada do denominador.
Então podemos tirar a raiz quadrada do denominador.
7. isolar X  subtraindo
subtraindo b 2 uma  em ambos os lados.
em ambos os lados.
 subtraindo
subtraindo  em ambos os lados.
em ambos os lados.
8. Escreva o lado direito sob um denominador comum. Isso não é como a fórmula abc, a fórmula para resolver uma equação quadrática na forma padrão. Isso funciona para qualquer  e dá
e dá  como resultado, que pode ser um número real ou complexo. Para verificar se esse processo funciona, basta seguir as etapas deste artigo na ordem inversa para reverter para o formulário padrão.
como resultado, que pode ser um número real ou complexo. Para verificar se esse processo funciona, basta seguir as etapas deste artigo na ordem inversa para reverter para o formulário padrão.
 e dá
e dá  como resultado, que pode ser um número real ou complexo. Para verificar se esse processo funciona, basta seguir as etapas deste artigo na ordem inversa para reverter para o formulário padrão.
como resultado, que pode ser um número real ou complexo. Para verificar se esse processo funciona, basta seguir as etapas deste artigo na ordem inversa para reverter para o formulário padrão.
Pontas
- É interessante notar que a fórmula abc também se aplica a coeficientes complexos, embora você tenha que simplificar um pouco mais para obter a resposta final, e as raízes não são pares conjugados. Problemas com expressões quadráticas são, no entanto, quase sempre dados com coeficientes reais.
Artigos sobre o tópico "Aprenda divisão quadrada"
Оцените, пожалуйста статью
Popular