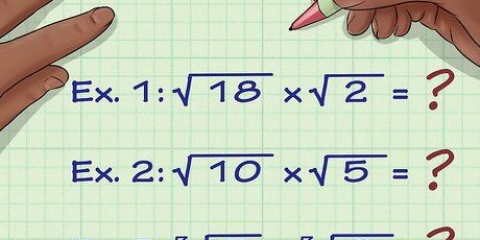Arredondando Números

Contente

Degraus
Pontas
Avisos

O arredondamento faz com que os números tenham menos casas decimais. Embora os números arredondados sejam menos precisos do que os números não arredondados, eles são preferidos em muitos casos. Dependendo da situação, pode ser necessário arredondar decimais ou inteiros. Se você quiser aprender a arredondar números, siga estas etapas.

Degraus

Método 1 de 3: arredondamento de decimais

1. Determine o número de casas decimais dos dígitos após o ponto decimal, para o qual você deve arredondar o número. Isso pode ser determinado pelo seu professor ou você pode inferir a partir do contexto e do tipo de números com os quais está lidando. Por exemplo, quando se trata de dinheiro, você provavelmente deseja arredondar para o centésimo ou para o centavo, enquanto com um peso você precisa arredondar para gramas.

Quanto menos preciso o número precisa ser, menos dígitos após o ponto decimal.
Quanto mais preciso, mais dígitos após o ponto decimal.

2. Determine o número de dígitos após o ponto decimal. é o número 10,7659 dado e você deseja arredondar para um milésimo, haverá 3 dígitos após o ponto decimal. Outra abordagem é arredondar o número para 5 dígitos significativos. Mas primeiro observe o 5 do número.

3. Encontre o número imediatamente à direita do número a ser arredondado (o 5). Esse é o número 9. Este número determina se o 5 é arredondado para cima ou para baixo.

4. Arredonde o dígito a ser arredondado (o dígito relevante) se o dígito à direita for 5, 6, 7, 8 ou 9. Isso é chamado de arredondamento, porque o número para o qual você arredonda é maior que o número a ser arredondado. A figura relevante 5, torna-se agora 6. Todos os dígitos à esquerda deste dígito permanecem os mesmos, e os dígitos à direita desaparecem (eles não importam mais, basta defini-los iguais a zero). Então, o número 10,7659 torna-se igual a após o arredondamento para o milésimo mais próximo 10.766.

Embora o 5 esteja no meio dos números 1-9, o número 5 precisa de outro número para decidir como arredondar. Embora seus professores nem sempre apliquem isso quando avaliam você!

5. Arredonde um dígito se o dígito à direita dele for 0, 1, 2, 3 ou 4. Isso significa que, para o número relevante, ele simplesmente permanece o mesmo, mesmo que isso seja chamado de arredondamento para baixo. Você nunca pode alterar um número para um número menor. Por exemplo, você tem o número 10,7653, então você arredondaria isso para baixo para 10.765 porque o grau 3 do lado direito do 5 é menor que 5.

Deixar tudo igual e definir os números à direita do dígito arredondado para zero torna o número final menor que o original.

Método 2 de 3: arredondando inteiros

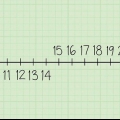
1. Arredonde um número para os próximos dez. Para fazer isso, olhe para o número à direita das dez. O dez é o segundo dígito, visto da direita para a esquerda, de um número. (Tome 12, então 1 é o dez.) Então, se esse número estiver entre 0-4, deixe o dígito para arredondar inalterado; se estiver entre 5-9, arredonde este número 1. aqui estão alguns exemplos:

12 --> 10
114 --> 110
57 --> 60
1.334 --> 1330
1.488 --> 1490
97--> 100

2. Arredonde um número para a próxima centena. Siga o mesmo protocolo de antes com os dez. Verifique a centena, o terceiro dígito de um número, à esquerda da dez. (No número 1.234, 2 é a centena). Em seguida, use o número à direita da centena, o dez, para determinar se deve arredondar para cima ou para baixo, com os números depois iguais a zero. aqui estão alguns exemplos:

7.891 -- > 7.900

15.753 --> 15.800

99. 961 --> 100.000

3.350 --> 3.300

450 --> 500

3. Arredonde um número para o próximo milhar. As mesmas regras se aplicam aqui novamente. Encontre o mil e depois verifique a centena antes de arredondar. Se o número estiver entre 0 e 4, arredonde para baixo e se estiver entre 5 e 9, arredonde para cima. Aqui estão mais alguns exemplos:

8.800 --> 9.000

1.015 --> 1.000

12.450 --> 12.000

333.878 --> 334.000

400.400 --> 400.000

Método 3 de 3: arredondando números para dígitos significativos

1. Tente entender o que é um número significativo. Considere um dígito significativo como um "interessante" ou um "importante" número que fornece informações úteis sobre um número. Isso significa que todos os zeros à direita dos inteiros ou à esquerda dos decimais podem ser omitidos, pois eles apenas preenchem o espaço. Para encontrar o número de dígitos significativos em um número, basta contar o número de dígitos da esquerda para a direita. Aqui estão alguns exemplos:

1.239 tem 4 dígitos significativos
134,9 tem 4 dígitos significativos
0,0165 tem 3 dígitos significativos

2. Arredondar um número para um número de dígitos significativos. Isso depende da tarefa em que você está trabalhando. Por exemplo, se você arredondar um número para dois dígitos significativos, tente reconhecer o segundo dígito significativo do número e use o número à direita para determinar se deve arredondar para cima ou para baixo. aqui estão alguns exemplos:

1,239 arredondado para 3 dígitos significativos é 1,24. Isso está correto porque o dígito à direita do terceiro dígito (3) é um 9 (mais de 5).

134,9 arredondado para 1 dígito significativo é 100. Isso está correto porque o dígito à direita da centena (1) é um 3 (menor que 5).

0.0165 arredondado para 2 dígitos significativos é 0.017. Isso está correto porque o segundo dígito significativo é igual a 6 e o número à direita é um 5, então arredondando para cima.

3. Arredonde para o número correto de algarismos significativos ao adicionar. Para fazer isso, é necessário primeiro somar os números fornecidos. Em seguida, encontre o número com o menor número de dígitos significativos e arredonde sua resposta para esse número. Veja como isso funciona:

13,214 + 234,6 + 7,0350 + 6,38=261,2290

Observe que o segundo número, 234,6, tem precisão de apenas um décimo e tem quatro dígitos significativos.

Arredonde a resposta para que ela tenha a mesma precisão, ou seja, para o décimo mais próximo ou para uma casa decimal. 261,2290 então se torna 261,2.

4. Arredonde para o número correto de dígitos significativos ao multiplicar. Primeiro multiplique todos os números dados. Em seguida, verifique qual dos números é arredondado para o menor número de dígitos significativos. Finalmente, arredonde a resposta com o mesmo grau de precisão que esse número. Veja como isso funciona:

16,235 × 0,217 × 5=17,614975

Observe que o número 5 tem apenas um dígito significativo. Isso significa que a resposta final pode ter apenas um dígito significativo.

17,614975 arredondado para um dígito significativo, em seguida, torna-se 20.

Pontas

É comum omitir os zeros à direita de um decimal após o arredondamento. Zeros à direita de um decimal não alteram o valor do número. É por isso que eles devem ser deixados de fora. Isso não se aplica a zeros à esquerda (antes) de um decimal.
Depois de encontrar o número relevante para arredondar, sublinhe-o. Isso garante que não haja confusão sobre o número que você vai arredondar e o número para o qual esse número relevante é arredondado.

Avisos

Certifique-se de estar familiarizado com a terminologia. A diferença entre dezenas e décimos, centenas e centésimos, decimais, decimais, significância etc...