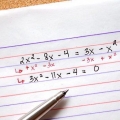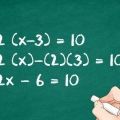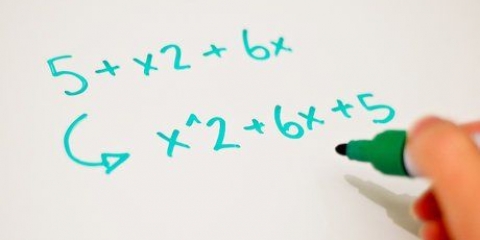Por exemplo, 

Por exemplo, para  dentro
dentro  para isolar, você puxa
para isolar, você puxa  fora de ambos os lados da equação a equação:
fora de ambos os lados da equação a equação:




Por exemplo, para  ser resolvido em
ser resolvido em  , divida cada lado da equação por
, divida cada lado da equação por  :
:



Então a solução de é é
é  .
. 

Por exemplo, reescrever  então se
então se  .
. 
Por exemplo,  .
. 
Por exemplo, para o polinômio quadrático  , você precisa encontrar dois números (
, você precisa encontrar dois números ( e
e  ), verdadeiro
), verdadeiro  e
e  .
. Porque você  você sabe que um dos números será negativo.
você sabe que um dos números será negativo. Você deveria ver isso  e
e  . Então você se divide
. Então você se divide  em
em  e reescreva o polinômio quadrático:
e reescreva o polinômio quadrático:  .
. 
Por exemplo, os dois primeiros termos do polinômio  são
são  . Um termo que ocorre em ambos é
. Um termo que ocorre em ambos é  . Este se torna o grupo dissolvido
. Este se torna o grupo dissolvido  .
. 
Por exemplo, os dois segundos termos no polinômio  são
são  . Um termo que ocorre em ambos é
. Um termo que ocorre em ambos é  . Assim é o grupo dissolvido
. Assim é o grupo dissolvido  .
. 
Por exemplo, depois de fatorar por agrupamento, . torna-se  igual a
igual a  .
. O primeiro binômio é  .
. O segundo binômio é  .
. Então o polinômio quadrático original,  pode ser escrito como a expressão fatorada
pode ser escrito como a expressão fatorada  .
. 
Por exemplo, para encontrar a primeira solução de  , defina a primeira expressão binomial igual a
, defina a primeira expressão binomial igual a  e te soltar
e te soltar  sobre. Por isso:
sobre. Por isso:



Então, a primeira solução do polinômio quadrático é
é  .
. 
Por exemplo, para encontrar a segunda solução para  , iguale a segunda expressão binomial a
, iguale a segunda expressão binomial a  e te soltar
e te soltar  sobre. Por isso:
sobre. Por isso:



Então a segunda solução do polinômio quadrático é igual a
igual a  .
.
Resolver polinômios
Contente
Um polinômio é uma expressão composta de adição e subtração de termos. Um termo pode consistir em variáveis, constantes e coeficientes. Ao resolver polinômios, você geralmente tenta descobrir para quais pontos x = 0. Polinômios de grau mais baixo têm uma ou duas soluções, dependendo se são polinômios lineares ou polinômios quadráticos. Esses tipos de polinômios podem ser facilmente resolvidos usando álgebra elementar e fatoração. Para resolver polinômios de alto grau, você pode ler artigos no wikiHow.
Degraus
Método 1 de 2: Resolvendo um polinômio linear

1. Determine se você está lidando com um polinômio linear. Um polinômio linear é um polinômio de primeiro grau. Isso significa que nenhuma variável terá um expoente (ou um expoente maior que 1). Como este é um polinômio de primeiro grau, ele tem exatamente uma solução.
- Por exemplo,
é um polinômio linear (ou polinômio), porque a variável
não tem expoente (que é o mesmo que um expoente de 1).

2. Faça a equação igual a zero. Este é um passo necessário para resolver todos os polinômios.


3. Mova o termo variável para um lado. Faça isso adicionando ou subtraindo a constante de ambos os lados da equação. Uma constante é um termo sem uma variável.
 dentro
dentro  para isolar, você puxa
para isolar, você puxa  fora de ambos os lados da equação a equação:
fora de ambos os lados da equação a equação:



4. Resolva a variável. Normalmente você tem que dividir cada lado da equação pela constante. Isso lhe dá a solução do polinômio.
 ser resolvido em
ser resolvido em  , divida cada lado da equação por
, divida cada lado da equação por  :
:


Então a solução de é
 é
é  .
.Método 2 de 2: Resolvendo um polinômio quadrático

1. Determine se você está lidando com um polinômio quadrático. Um polinômio quadrático é uma equação quadrática. Isso significa que nenhuma variável tem um expoente maior que 2. Como este é um polinômio de segundo grau, existem duas soluções.
- Por exemplo,
é um polinômio quadrático, porque a variável
uma
tem como expoente.

2. Certifique-se de que o polinômio está escrito em ordem de grau. Isso significa que o termo com expoente  é listado primeiro seguido pelo termo de primeiro grau, então a constante.
é listado primeiro seguido pelo termo de primeiro grau, então a constante.
 é listado primeiro seguido pelo termo de primeiro grau, então a constante.
é listado primeiro seguido pelo termo de primeiro grau, então a constante. então se
então se  .
.
3. Faça a equação igual a zero. Este é um passo necessário para resolver todos os polinômios.
 .
.
4. Reescreva a expressão como uma expressão de quatro termos. Você faz isso dividindo o termo de primeiro grau (de  prazo). Você está procurando dois números cuja soma é igual ao coeficiente de primeiro grau e cujo produto é igual à constante.
prazo). Você está procurando dois números cuja soma é igual ao coeficiente de primeiro grau e cujo produto é igual à constante.
 prazo). Você está procurando dois números cuja soma é igual ao coeficiente de primeiro grau e cujo produto é igual à constante.
prazo). Você está procurando dois números cuja soma é igual ao coeficiente de primeiro grau e cujo produto é igual à constante. , você precisa encontrar dois números (
, você precisa encontrar dois números ( e
e  ), verdadeiro
), verdadeiro  e
e  .
. você sabe que um dos números será negativo.
você sabe que um dos números será negativo. e
e  . Então você se divide
. Então você se divide  em
em  e reescreva o polinômio quadrático:
e reescreva o polinômio quadrático:  .
.
5. Fator por agrupamento. Você faz isso fatorando um termo que corresponda às duas primeiras condições no polinômio.
 são
são  . Um termo que ocorre em ambos é
. Um termo que ocorre em ambos é  . Este se torna o grupo dissolvido
. Este se torna o grupo dissolvido  .
.
6. Fatore o segundo grupo. Você faz isso fatorando um termo que ocorre nos dois segundos termos do polinômio.
 são
são  . Um termo que ocorre em ambos é
. Um termo que ocorre em ambos é  . Assim é o grupo dissolvido
. Assim é o grupo dissolvido  .
.
7. Reescreva o polinômio como dois binômios. Um binômio é uma expressão com dois termos. Você já tem um binômio, a expressão entre parênteses para cada grupo. Esta expressão deve ser a mesma para todos os grupos. O segundo binômio é feito combinando os dois termos fatorados de cada grupo.
 igual a
igual a  .
. .
. .
. pode ser escrito como a expressão fatorada
pode ser escrito como a expressão fatorada  .
.
8. Encontre a solução primeiro. Você faz isso resolvendo  no primeiro binômio.
no primeiro binômio.
 no primeiro binômio.
no primeiro binômio. , defina a primeira expressão binomial igual a
, defina a primeira expressão binomial igual a  e te soltar
e te soltar  sobre. Por isso:
sobre. Por isso:


Então, a primeira solução do polinômio quadrático
 é
é  .
.
9. Determine a segunda solução. Você faz isso por  resolver no segundo binômio.
resolver no segundo binômio.
 resolver no segundo binômio.
resolver no segundo binômio. , iguale a segunda expressão binomial a
, iguale a segunda expressão binomial a  e te soltar
e te soltar  sobre. Por isso:
sobre. Por isso:


Então a segunda solução do polinômio quadrático é
 igual a
igual a  .
.Pontas
- Não se preocupe com variáveis, como t, ou se você tiver uma equação que equivale a f(x) em vez de 0. Se a questão quiser ver raízes, zeros ou fatores, trate-a como qualquer outro problema.
- Lembre-se da ordem das operações enquanto trabalha - limpando os parênteses primeiro, depois fazendo a multiplicação e a divisão e, finalmente, a adição e a subtração.
Artigos sobre o tópico "Resolver polinômios"
Оцените, пожалуйста статью
Popular