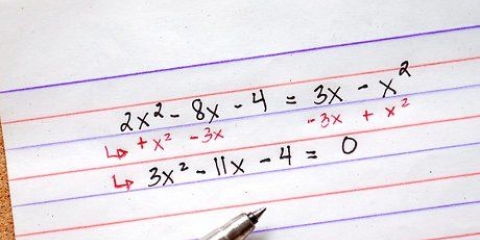Se o movimento o levar a uma "caixa" acima do quadrado mágico, fique na coluna dessa caixa, mas coloque o número na linha inferior dessa coluna. Se o movimento o levar a uma caixa à direita do quadrado mágico, permaneça nessa linha, mas coloque o número na coluna dessa linha, à esquerda do quadrado. Se a movimentação o levar para uma caixa que já possui um número, volte para a caixa anterior que foi preenchida e coloque o próximo número diretamente acima dela. 

soma = [6 * (62 + 1)] / 2 soma = [6 * (36 + 1)] / 2 soma = (6 * 37) / 2 soma = 222 / 2 A constante mágica de um quadrado 6x6 é 222/2, ou 111. Todas as linhas, colunas e diagonais devem ser somadas para obter esse número. 
Então, para cada quadrado 6x6, cada quadrante se torna um quadrado 3x3. 
No exemplo de um quadrado 6x6, o Quadrante A é resolvido com os números de 1 a 9; Quadrante B com os de 10-18; Quadrante C com 19-27 e Quadrante D com 28-36. 
Trate o primeiro número de cada quadrante como se fosse um. Coloque-o na caixa do meio na linha superior de cada quadrante. Trate cada quadrante como um pequeno quadrado mágico. Mesmo que a caixa esteja disponível em um quadrante adjacente, ignore-a e pule para a `regra de exceção` que se encaixa nessa situação. 
Use um lápis para marcar todos os quadrados na linha superior até chegar à caixa do meio do Quadrante A. Então, em um quadrado 6x6 você marca a caixa 1 (com o número 8), mas em um quadrado 10x10 você marca as caixas 1 e 2 (com os números 17 e 24, respectivamente). Marque um quadrado usando as caixas que você acabou de marcar como a linha superior. Se você marcou apenas uma caixa, seu quadrado não consistirá em mais de uma caixa. Chamamos isso de Marcação A-1. Assim, em um quadrado mágico de 10x10, o marcador A-1 é composto pelas caixas 1 e 2 nas linhas 1 e 2, criando um quadrado de 2x2 no quadrante superior esquerdo. Na linha imediatamente abaixo do Marcador A-1, pule o número na primeira coluna e marque quantas caixas de lado a lado você indicou no Marcador A-1. Chamamos essa linha do meio de Marcação A-2. A seleção A-3 é uma caixa semelhante a A-1, mas colocada no canto inferior esquerdo do quadrante. Seleção A-1, A-2 e A-3 juntos formam o Marcador A. Repita este processo no Quadrante D, criando uma área de marcador idêntica, Marcador D. 

Aqui estão duas imagens de um Magic Square 14x14 antes e depois de ambos os switches. A superfície de comutação do Quadrante A está marcada em azul, a superfície do Quadrante D é verde, para o Quadrante C amarela e para o Quadrante B laranja. Magic Square de 14x14 antes da troca (passos 6, 7 e 8) Quadrado Mágico de 14x14 após realizar as substituições (passos 6, 7 e 8) 

soma = [4 * (42 + 1)] / 2 soma = [4 * (16 + 1)] / 2 soma = (4 * 17) / 2 soma = 68 / 2 A constante mágica de um quadrado 4x4 é 68/2, ou 34. Todas as linhas, colunas e diagonais devem formar este número. 
Em um quadrado 4x4, basta marcar os quatro quadrados de canto. Em um quadrado de 8x8, cada Marcador é uma área de 2x2 nos cantos. Em um quadrado de 12x12, cada Marcador é uma área de 3x3 nos cantos, etc. 
Em um quadrado 4x4, o Marcador Central é uma área 2x2 no centro. Em um quadrado de 8x8, o Marcador Central é uma área de 4x4 no centro, etc. 
1 na caixa superior esquerda e 4 na caixa superior direita 6 e 7 nas caixas do meio na Linha 2 10 e 11 nas caixas do meio na linha 3 13 na caixa inferior esquerda e 16 na caixa inferior direita. 
15 e 14 nas caixas do meio na Linha 1 12 na caixa mais à esquerda e 9 na caixa mais à direita na Linha 2 8 na caixa mais à esquerda e 5 na caixa mais à direita na linha 3 3 e 2 nas caixas do meio na Linha 4 Neste ponto, todas as colunas, linhas e diagonais devem ter uma soma igual à constante mágica calculada anteriormente.
Resolva quadrados mágicos
Contente
Os quadrados mágicos só cresceram em popularidade desde o surgimento de jogos baseados em matemática como o Sudoku. Um quadrado mágico é um arranjo de números em um quadrado de tal forma que a soma de cada linha, coluna e diagonal seja um número constante, a chamada constante mágica. Este artigo vai explicar como resolver qualquer tipo de quadrado mágico, seja um quadrado ímpar, par simples ou par duplo.
Degraus
Método 1 de 3: Resolvendo um quadrado mágico ímpar

1. Calcule a constante mágica. Você pode encontrar esse número usando uma fórmula matemática simples, onde n = o número de linhas ou colunas em seu quadrado mágico. Assim, por exemplo, em um quadrado mágico 3x3, n = 3. A constante mágica = [n * (n2 + 1)] / 2. Então, no exemplo do quadrado 3x3:
- soma = [3 * (32 + 1)] / 2
- soma = [3 * (9 + 1)] / 2
- soma = (3 * 10) / 2
- soma = 30 / 2
- A constante mágica de um quadrado 3x3 é 30/2, ou 15.
- Todas as linhas, colunas e diagonais têm esse número como soma.

2. Coloque o número 1 na caixa do meio da linha superior. Este é sempre o ponto em que você começa se o seu quadrado mágico de lados tiver um número ímpar de lados, não importa quão grande ou pequeno esse número seja. Então, se você tem um quadrado 3x3, coloque o número 1 na caixa 2; em um quadrado de 15x15, coloque o número 1 na caixa 8.

3. Preencha os números restantes em um padrão um para cima, um para a direita. Você sempre preenche os números de acordo com uma série (1, 2, 3, 4, etc.).) subindo uma linha e depois uma coluna à direita. Você percebe imediatamente que ao colocar o número 2 você acaba acima da linha superior, fora do quadrado mágico. Tudo bem - embora você sempre siga o método de um para o outro, há três exceções que também seguem um padrão previsível:
Método 2 de 3: Resolvendo um quadrado mágico par simples

1. Entenda o que é um simples quadrado par. Todo mundo sabe que um número par é divisível por 2, mas com quadrados mágicos existem métodos diferentes para resolver quadrados pares simples e duplos.
- Um quadrado par simples tem um número de quadrados por lado que é divisível por 2, mas não por 4.
- O menor quadrado mágico par é 6x6, porque 2x2 quadrados mágicos não podem ser feitos.

2. Calcule a constante mágica. Use o mesmo método que usaria para quadrados mágicos ímpares: a constante mágica = [n * (n2 + 1)] / 2, onde n = o número de quadrados por lado. Então, no exemplo de um quadrado 6x6:

3. Divida o quadrado mágico em quatro quadrantes de tamanhos iguais . Rotule-os A (superior esquerdo), C (superior direito), D (inferior esquerdo) e B (inferior direito). Para determinar o tamanho de cada quadrado, divida o número de caixas em cada linha ou coluna pela metade.

4. Atribuir um intervalo de números a cada quadrante. O quadrante A recebe um quarto dos números; Quadrante B no segundo trimestre; Quadrante C o terceiro trimestre e Quadrante D o último quarto do intervalo total de números de um quadrado mágico 6x6.

5. Resolva cada quadrante usando o método do quadrado mágico com um número ímpar de caixas por lado. O quadrante A é fácil de preencher, pois começa com o número 1, como os quadrados mágicos costumam fazer. Os quadrantes B-D, no entanto, começam com números ímpares - 10, 19 e 28, como no nosso exemplo.

6. Faça os marcadores A e D. Se você tentou adicionar colunas, linhas e diagonais imediatamente, notou que elas não somam a constante mágica. Você precisará trocar algumas caixas dos quadrantes superior esquerdo e inferior esquerdo para completar seu quadrado mágico. Chamamos essas áreas de Marcador A e Marcador D.

7. Trocar os marcadores A e D. Esta é uma troca de 1 para 1. Mova as caixas entre o Quadrante A e o Quadrante D sem alterar a ordem. Depois de ter feito isso, todas as linhas, colunas e diagonais em seu quadrado mágico devem ter a constante mágica calculada anteriormente como sua soma.

8. Troque uma vez extra por quadrados mágicos individuais maiores que 6x6. Além da troca para os quadrantes A e D mencionados acima, você também precisa fazer uma troca para os quadrantes C e B. Marque as colunas do lado direito do quadrado para a esquerda, uma a menos que o número de colunas marcadas para destaque A-1. Troque os valores do Quadrante C pelos valores do Quadrante B dessas colunas, usando o mesmo método de um para um.
Método 3 de 3: Resolvendo um quadrado mágico par duplo

1. Entenda o que é um quadrado par duplo. Um quadrado par simples tem um número de quadrados por lado que é divisível por 2. Um quadrado par duplo tem um número de quadrados por lado que são divisíveis por 4.
- O menor quadrado duplamente par que pode ser feito é o quadrado 4x4.

2. Calcule a constante mágica. Use o mesmo método que para os quadrados mágicos ímpares ou pares singulares: a constante mágica = [n * (n2 + 1)] / 2, onde n = o número de quadrados por lado. Então, no exemplo de um quadrado 4x4:

3. Aplicar marcadores A-D. Em cada canto do quadrado mágico, coloque um pequeno quadrado com lados de n/4, onde n = o comprimento de um lado de todo o quadrado mágico. No sentido anti-horário, rotule-os como Marcadores A, B, C e D.

4. Coloque a Marca Central. Marque todas as caixas no centro do quadrado mágico em uma área quadrada de comprimento n/2, onde n = o comprimento de cada lado de um quadrado mágico completo. O Marcador Central não deve se sobrepor aos Marcadores A-D, mas deve tocá-los nos cantos.

5. Preencha o quadrado mágico, mas apenas nas áreas marcadas. Comece a preencher seus números quadrados mágicos da esquerda para a direita, mas só coloque um número se a caixa estiver dentro de um marcador. Então, em uma caixa 4x4, preencha as seguintes caixas:

6. Preencha o resto do quadrado mágico contando para trás. Este é essencialmente o inverso do passo anterior. Comece novamente com a caixa superior esquerda, mas desta vez pule todas as caixas que caem na área marcada e preencha as caixas não selecionadas contando para trás. Comece com o maior número em seu intervalo de números. Então, em um quadrado mágico 4x4, preencha:
Pontas
- Experimente variações dessas etapas para descobrir seus próprios métodos de solução.
Necessidades
- Lápis
- Papel
- Apagador
Artigos sobre o tópico "Resolva quadrados mágicos"
Оцените, пожалуйста статью
Popular