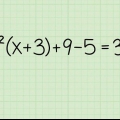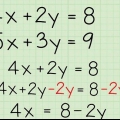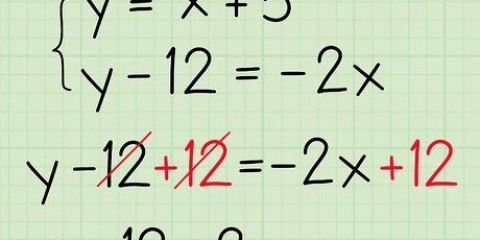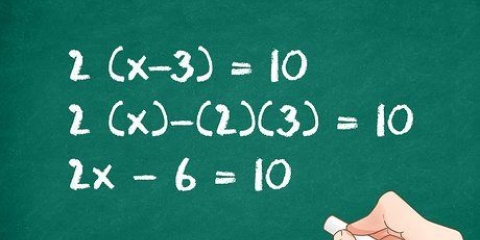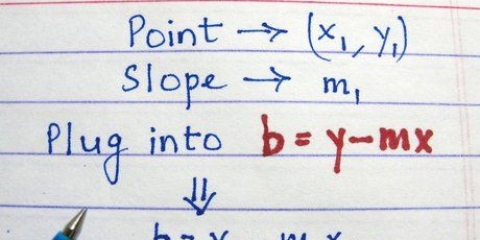Resolva uma equação em duas etapas

Contente

Degraus
Pontas

Equações que você pode resolver em duas etapas são relativamente fáceis – afinal, são necessárias apenas duas etapas. Para resolver tal equação, tudo o que você precisa fazer é isolar a variável adicionando, subtraindo, multiplicando ou dividindo. Se você quiser saber como e de que maneira resolver equações em duas etapas, siga as instruções abaixo.

Degraus

Método 1 de 3: Resolvendo equações com uma variável

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 1

1. Anote o problema. O primeiro passo para resolver tal equação é escrevê-la para que você possa ter uma visão melhor do problema. Suponha que temos o seguinte problema: -4x + 7 = 15.

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 2

2. Decida se deve usar adição ou subtração para isolar o termo solicitado. O próximo passo é encontrar uma maneira de deixar -4x de um lado e as constantes (os inteiros) do outro lado. Para fazer isso, você precisa encontrar o oposto de +7, que é -7. Subtraia 7 de ambos os lados da equação para eliminar o +7 que está do mesmo lado da variável. Basta escrever -7 abaixo de 7 de um lado e abaixo de 15 do outro lado para que a equação fique certa em ambos os lados.

Lembre-se da regra de ouro da álgebra. O que você faz de um lado da equação, você tem que fazer do outro lado, para acertar. Portanto, 7 também foi subtraído de 15. O 7 só precisa ser subtraído uma vez por lado. Portanto, não é subtraído de -4x.

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 3

3. Aumente ou diminua a equação em ambos os lados. Depois disso, a variável é isolada. Subtrair 7 do lado esquerdo da equação torna este lado 0, deixando 8 no lado direito da equação. Então a nova equação se torna -4x = 8.

-4x + 7 = 15 =

-4x = 8

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 4

4. Remova o coeficiente da variável multiplicando ou dividindo. O coeficiente é o número associado à variável. Neste exemplo, o coeficiente é -4. Para remover -4 de -4x, divida ambos os lados da equação por -4.

Novamente, o que você faz de um lado da equação, você deve fazer do outro lado.É por isso que diz duas vezes ÷ -4.

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 5

5. Resolva para a variável. Para fazer isso, divida o lado esquerdo da equação por -4 para obter x. Divida o lado direito da equação por -4 para obter -2.Então, x = -2. Agora você resolveu a equação em duas etapas - subtração e divisão.

Método 2 de 3: Resolva equações com uma variável em cada lado

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 6

1. Escreva a tarefa. O problema que você vai trabalhar é o seguinte: -2x - 3 = 4x - 15. Antes de continuar: certifique-se de que ambas as variáveis são iguais entre si. Nesse caso, -2x e 4x têm a mesma variável x, então você pode continuar.

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 7

2. Traga ambas as constantes para o lado direito da equação. Para fazer isso você precisa adicionar ou subtrair para que você possa remover a constante do lado esquerdo da equação. A constante é -3, então você precisa usar o oposto, +3, e adicionar essa constante aos dois lados da equação.

Adicionando +3 ao lado esquerdo da equação, -2x -3, dá (-2x -3) + 3, ou -2x à esquerda.

Adicionando +3 ao lado direito da equação, 4x -15, dá (4x - 15) +3, ou 4x -12.

Então, (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12

A nova equação é -2x = 4x -12

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 8

3. Mova as variáveis para o lado esquerdo da equação. Para fazer isso, você só precisa subtrair -4x de ambos os lados da equação. À esquerda, -2x - 4x = -6x, e à direita, (4x -12) -4x = -12. Isso torna a nova equação: -6x = -12

-2x - 4x = (4x - 12) - 4x = -6x = -12

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 9

4. Resolva para a variável. Agora que você simplificou a equação para -6x = -12, tudo que você precisa fazer é dividir ambos os lados da equação por -6 para isolar a variável x, que é multiplicada por -6. No lado esquerdo da equação, -6x ÷ -6 = x, e no lado direito, -12 ÷ -6 = 2. então, x = 2.

-6x -6 = -12 ÷ -6

x = 2

Método 3 de 3: Outras maneiras de resolver uma equação de duas etapas

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 10

1. Resolva equações em duas etapas, mantendo a variável no lado direito da equação.Contanto que você isole a variável, você obtém a mesma resposta. Vamos dar uma olhada no próximo problema, 11 = 3 - 7x.Para resolver isso, o primeiro passo é combinar o dinheiro subtraindo 3 de ambos os lados da equação. Então você tem que dividir ambos os lados por -7 para resolver x. Abaixo você pode ver como isso acontece:

11 = 3 - 7x =
11 - 3 = 3 - 3 - 7x =
8 = - 7x =
8/-7 = -7/7x
-8/7 = x ou -1.14 = x

Imagem intitulada Resolver Equações Algébricas em Dois Passos Passo 11

2. Resolva uma equação de duas etapas multiplicando em vez de dividir no final. O princípio para resolver esse tipo de equação é o mesmo: combine as constantes entre si e então isole a variável sem termo. Vamos tomar o seguinte problema como exemplo, x/5 + 7 = -3. A primeira coisa a fazer é subtrair 7 de ambos os lados da equação, depois multiplicar ambos os lados por 5 para resolver x. Veja como você pode fazer isso:

x/5 + 7 = -3 =

(x/5 + 7) - 7 = -3 - 7 =

x/5 = -10

x/5 * 5 = -10 * 5

x = -50

Pontas

Se não houver nenhum número na frente de x, assuma que é 1x.
Não pode haver nenhuma constante em ambos os lados da equação. Se não houver nenhum número após x, suponha que o seguinte seja válido: `x + 0`.