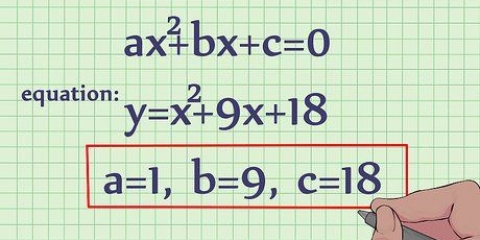Instruções gratuitas passo a passo 
3x + 2x - 8 
6x + 13x + 6 
8x + 10x + 2 
27x - 12 = 0 
x + 4x + 1 = 0 
y = x − x − 2 
Se você não consegue ver onde a parábola cruza com o eixo x, pressione [2nd] e depois [TRACE]. Pressione [2] ou selecione "zero". Mova o cursor para a esquerda de uma interseção e pressione [ENTER]. Mova o cursor para o lado direito de uma interseção e pressione [ENTER]. Mova o cursor o mais próximo possível da interseção e pressione [ENTER]. A calculadora indicará o valor x.Faça o mesmo para o outro ponto de interseção. 
Fatorando equações do segundo grau
Contente
Um polinômio contém uma variável (x) elevada a uma certa potência e vários termos e/ou constantes. Para fatorar um polinômio, você precisará dividir a expressão em expressões menores que são multiplicadas. Isso requer um certo nível de matemática e, portanto, pode ser difícil de entender se você ainda não estiver tão longe.
Degraus
Método 1 de 7: Introdução
1. A equação. O formato padrão para uma equação quadrática é:
ax + bx + c = 0
Comece ordenando os termos em sua equação da maior para a menor potência. Por exemplo, pegue:
6 + 6x + 13x = 0
Vamos reorganizar essa expressão para facilitar o trabalho - simplesmente movendo os termos:
6x + 13x + 6 = 0
Comece ordenando os termos em sua equação da maior para a menor potência. Por exemplo, pegue:
Vamos reorganizar essa expressão para facilitar o trabalho - simplesmente movendo os termos:
2. Encontre os fatores usando um dos métodos abaixo. A fatoração do polinômio resultará em duas expressões menores que podem ser multiplicadas para obter o polinômio original:
6x + 13x + 6 = (2x + 3)(3x + 2)
Neste exemplo, (2x +3) e (3x + 2) são fatores da expressão original, 6x + 13x + 6.
Neste exemplo, (2x +3) e (3x + 2) são fatores da expressão original, 6x + 13x + 6.
3. Verifique seu trabalho! Multiplique os fatores que você encontrou. Combine os termos semelhantes e pronto. Começar com:
(2x + 3)(3x + 2)
Vamos testar isso, multiplicando os termos usando EBBL (primeiro - externo - interno - último), o que nos dá:
6x + 4x + 9x + 6
Agora somamos 4x e 9x porque são termos iguais. Sabemos que os fatores estão corretos porque voltamos a equação com a qual começamos:
6x + 13x + 6
Vamos testar isso, multiplicando os termos usando EBBL (primeiro - externo - interno - último), o que nos dá:
Agora somamos 4x e 9x porque são termos iguais. Sabemos que os fatores estão corretos porque voltamos a equação com a qual começamos:
Método 2 de 7: tentativa e erro
Se você tiver um polinômio bastante simples, poderá ver imediatamente quais são os fatores. Por exemplo, depois de alguma prática, muitos matemáticos são capazes de ver que a expressão 4x + 4x + 1 tem os fatores (2x + 1) e (2x + 1) só porque já viram isso tantas vezes. (Obviamente isso não será tão fácil com polinômios mais complicados.) Vamos usar uma expressão menos padrão para este exemplo:
1. Anote os fatores de uma termo e o c prazo. Utilize o formato ax + bx + c = 0, reconhecer o uma e c termos e observe quais fatores existem. Para 3x + 2x - 8, isso significa:
a = 3 e tem 1 par de fatores: 1 * 3
c = -8 e tem 4 pares de fatores: -2 * 4, -4 * 2, -8 * 1 e -1 * 8.
2. Escreva dois pares de colchetes com um espaço vazio. Aqui você insere as constantes de cada expressão:
(x)(x)
3. Preencha o espaço na frente dos x`s com alguns possíveis fatores do uma onde o. Para o uma termo em nosso exemplo, 3x, há apenas 1 possibilidade:
(3x)(1x)
4. Preencha os 2 espaços após os x com alguns fatores para as constantes. Suponha que escolhemos 8 e 1. Digite isto:
(3x 8)(X 1)
5. Determine quais sinais (mais ou menos) devem ser colocados entre as variáveis x e os números. Dependendo dos sinais da expressão original, é possível descobrir quais devem ser os sinais das constantes. Vamos pegar as duas constantes dos dois fatores h e k mencionar:
Se ax + bx + c então (x + h)(x + k)
Se ax - bx - c ou ax + bx - c então (x - h)(x + k)
Se ax - bx + c então (x - h)(x - k)
Em nosso exemplo, 3x + 2x - 8, o sinal é:(x - h)(x + k), o que nos dá os dois fatores a seguir:
(3x + 8) e (x - 1)
Em nosso exemplo, 3x + 2x - 8, o sinal é:(x - h)(x + k), o que nos dá os dois fatores a seguir:
6. Teste sua escolha com a multiplicação primeiro-exterior-interno-último. Um primeiro teste rápido para ver se o termo médio é pelo menos o valor certo. Se não, então você provavelmente está errado c fatores escolhidos. Vamos testar a resposta:
(3x + 8)(x - 1)
Por multiplicação obtemos:
3x - 3x + 8x - 8
Simplifique esta expressão adicionando os termos semelhantes (-3x) e (8x), e obtemos:
3x - 3x + 8x - 8 = 3x + 5x - 8
Agora sabemos que pegamos os fatores errados:
3x + 5x - 8 3x + 2x - 8
Por multiplicação obtemos:
Simplifique esta expressão adicionando os termos semelhantes (-3x) e (8x), e obtemos:
Agora sabemos que pegamos os fatores errados:
7. Troque suas escolhas, se necessário. Em nosso exemplo, vamos tentar 2 e 4, em vez de 1 e 8:
(3x + 2)(x - 4)
Agora nosso c termo igual a -8, mas o produto externo/interno de (3x * -4) e (2 * x) é -12x e 2x, o que não é o correto b termo ou +2x obtém.
-12x + 2x = 10x
10x 2x
Agora nosso c termo igual a -8, mas o produto externo/interno de (3x * -4) e (2 * x) é -12x e 2x, o que não é o correto b termo ou +2x obtém.
8. Inverta a ordem se necessário. Vamos tentar virar 2 e 4:
(3x + 4)(x - 2)
Agora nosso c termo (4 * 2 = 8) e ainda OK, mas os produtos externos/internos são -6x e 4x.Combinando estes temos:
-6x + 4x = 2x
2x -2x Estamos chegando bem perto do 2x onde queremos estar, mas o sinal ainda não está certo.
Agora nosso c termo (4 * 2 = 8) e ainda OK, mas os produtos externos/internos são -6x e 4x.Combinando estes temos:
9. Verifique novamente seus personagens, se necessário. Mantemos essa ordem, mas trocamos com o sinal de menos:
(3x - 4)(x + 2)
Agora o c prazo ainda ok, e os produtos externos/internos agora são (6x) e (-4x). Porque:
6x - 4x = 2x
2x = 2x Agora vemos o 2x positivo de volta do problema original. Estes devem ser os fatores certos.
Agora o c prazo ainda ok, e os produtos externos/internos agora são (6x) e (-4x). Porque:
Método 3 de 7: Decomposição
Este método fornece todos os fatores possíveis de uma e c termos e usá-los para descobrir quais fatores estão corretos. Se os números forem muito grandes ou a adivinhação de outros métodos demorar muito, use desta maneira. Um exemplo:
1. Multiplique o uma termo com o c prazo. Neste exemplo,, uma é 6 e c também é 6.
6 * 6 = 36
2. Encontre o b termo por fatoração e teste. Estamos procurando 2 números que são fatores de uma * c , e juntos o b termo (13) formulário.
4 * 9 = 36
4 + 9 = 13
3. Substitua os dois números que você obtém em sua equação como a soma dos b prazo. Vamos k e h para representar os 2 números que temos, 4 e 9:
ax + kx + hx + c
6x + 4x + 9x + 6
4. Fatorar o polinômio por agrupamento. Organize a equação para que você possa isolar o máximo divisor comum dos dois primeiros termos e dos dois últimos termos. Ambos os fatores devem ser os mesmos. Some os GCDs e coloque-os entre parênteses, ao lado dos fatores; como resultado, você obtém os dois fatores:
6x + 4x + 9x + 6
2x(3x + 2) + 3(3x + 2)
(2x + 3)(3x + 2)
Método 4 de 7: Triple Play
Semelhante ao método de decomposição. O método `triple play` examina os possíveis fatores do produto de uma e c e usá-lo para descobrir o que b devemos ser. Tome a equação como exemplo:
1. Multiplique o uma termo com o c prazo. Tal como acontece com o método de decomposição, usamos isso para determinar os candidatos para o b prazo. Neste exemplo: uma é 8 e c é 2.
8 * 2 = 16
2. Encontre os 2 números com este número como produto e com uma soma igual ao b prazo. Esta etapa é equivalente ao método de decomposição - testamos candidatos para as constantes. O produto do uma e c termos é 16, e o c termo é 10:
2 * 8 = 16
8 + 2 = 10
3. Pegue esses 2 números e substitua-os na fórmula `triple play`. Pegue os 2 números do passo anterior - vamos colocá-los h e k chame-os - e coloque-os na expressão:
((ax + h)(ax + k))/a
Com isso obtemos:
((8x + 8)(8x + 2)) / 8
Com isso obtemos:
4. Veja qual dos dois termos no denominador pode ser completamente dividido por uma. Neste exemplo, estamos vendo se (8x + 8) ou (8x + 2) pode ser dividido por 8. (8x + 8) é divisível por 8, então dividimos este termo por uma e vamos deixar o outro em paz.
(8x + 8) = 8(x + 1)
O termo que mantivemos aqui é o que sobra depois de dividir pelo uma termo: (x + 1)
O termo que mantivemos aqui é o que sobra depois de dividir pelo uma termo: (x + 1)
5. Pegue o máximo divisor comum (mdc) de um ou de ambos os termos, se possível. Neste exemplo, vemos que o segundo termo tem um mdc de 2, porque 8x + 2 = 2(4x + 1). Combine esta resposta com o termo que você descobriu na etapa anterior. Estes são os fatores da sua equação.
2(x + 1)(4x + 1)
Método 5 de 7: A diferença entre dois quadrados
Alguns coeficientes em um polinômio podem ser reconhecidos como `quadrados`, ou também como o produto de 2 dos mesmos números. Ao descobrir quais são esses quadrados, você poderá fatorar os polinômios muito mais rapidamente. Tomamos a equação:
1. Remova o mdc da equação, se possível. Neste caso vemos que 27 e 12 são ambos divisíveis por 3, então podemos colocá-los separadamente:
27x - 12 = 3(9x - 4)
2. Determine se os coeficientes da sua equação são quadrados. Para usar este método é necessário ser capaz de determinar a raiz dos termos. (Observe que omitimos os decimais - como esses números são quadrados, eles podem ser o produto de 2 números negativos)
9x = 3x * 3x e 4 = 2 * 2
3. Usando a raiz quadrada que você determinou, agora você pode escrever os fatores. Nós pegamos o uma e c valores da etapa anterior: uma = 9 e c = 4, então as raízes disso são: - √uma = 3 ec = 2. Estes são os coeficientes das expressões fatoradas:
27x - 12 = 3(9x - 4) = 3(3x + 2)(3x - 2)
Método 6 de 7: A Fórmula ABC
Se nada parecer funcionar e você não puder fatorar a equação, use a fórmula abc. Tome o seguinte exemplo:
1. Preencha os valores correspondentes, na fórmula abc:
x = -b ± √(b - 4ac)
---------------------
2a
Agora temos a expressão:
x = -4 ± √(4 - 4•1•1) / 2
---------------------
2a
Agora temos a expressão:
2. Resolva para x. Agora você deve obter 2 valores para x. Estes são:
x = -2 + √(3) ou x = -2 - √(3)
x = -2 + √(3) ou x = -2 - √(3)
3. Use os valores de x para determinar os fatores. Preencha os valores x obtidos nas duas equações, como constantes. Esses são seus fatores. Se respondermos as duas h e k então escrevemos os dois fatores da seguinte forma:
(x - h) (x - k)
Neste caso, a resposta final é:
(x - (-2 + √(3))(x - (-2 - √(3))) = (x + 2 - √(3))(x + 2 + √(3))
Neste caso, a resposta final é:
Método 7 de 7: Use uma calculadora
Se for permitido (ou obrigatório) usar uma calculadora gráfica, isso torna a fatoração muito mais fácil, especialmente durante exames e exames. As instruções a seguir são para uma calculadora gráfica TI. Usamos a equação do exemplo:
1. Digite a equação em sua calculadora. Você usará o solucionador de equações, também conhecido como tela [Y = ].
2. Faça o gráfico da equação com a calculadora. Depois de inserir a equação, pressione [GRAPH] - agora você deve ver uma linha curva, uma parábola como representação gráfica de sua equação (e é uma parábola, porque estamos lidando com um polinômio).
3. Encontre onde a parábola cruza com o eixo x. Como uma equação quadrática é tradicionalmente notada como ax + bx + c = 0, esses são os dois valores de x que tornam a equação igual a zero:
(-1, 0), (2, 0)
x = -1, x = 2
4. Insira os valores de x que você obteve, nas duas expressões fatoradas. Se tomarmos os dois valores de x h e k escreva-o como um termo, então a expressão que usamos fica assim:
(x - h)(x - k) = 0
Então nossos dois fatores se tornam:
(x - (-1))(x - 2) = (x + 1)(x - 2)
Então nossos dois fatores se tornam:
Pontas
- Se você fatorou o polinômio com a fórmula abc e sua resposta contém raízes, você pode converter os valores de x em frações para verificá-los.
- Se um termo não tem coeficiente na frente dele, então o coeficiente é igual a 1, por exemplo. x = 1x.
- Se você tem uma calculadora TI-84, existe um programa chamado SOLVER que pode resolver uma equação quadrática para você. Isso também resolve polinômios de grau mais alto.
- Depois de muita prática, você acabará conseguindo resolver polinômios de cor. Mas só para ter certeza, é melhor sempre escrevê-los.
- Se um termo não existe, então o coeficiente é igual a zero. Então pode ser útil reescrever a equação. Por exemplo. x + 6 = x + 0x + 6.
Avisos
- Quando você aprender esse conceito na aula de matemática, preste atenção ao que o professor explica e não use apenas seu método favorito. Você pode ser solicitado a usar um método específico em um teste, ou calculadoras gráficas podem não ser permitidas.
Necessidades
- Lápis
- Papel
- Equação quadrática (também chamada de equação quadrática)
- Calculadora gráfica (opcional)
Artigos sobre o tópico "Fatorando equações do segundo grau"
Оцените, пожалуйста статью
Popular
