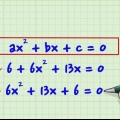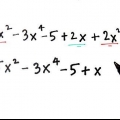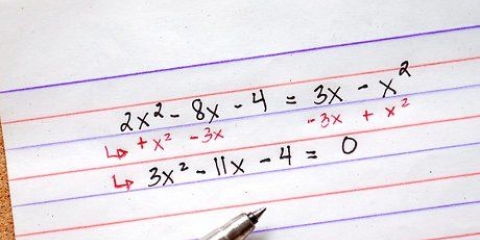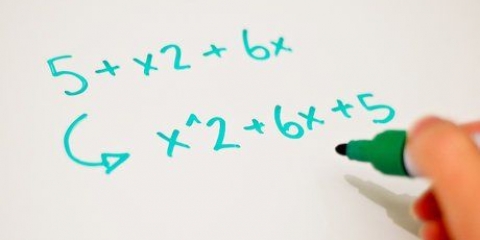Em (x + 3x), vemos que x é igual. Em (-6x - 18), vemos que -6 é igual. 
Fatorando x obtemos x(x + 3). Decompondo -6 da segunda peça, obtemos -6(x + 3). 
Isso dá (x + 3)(x - 6). 
As soluções são -3 e √6. 

Fatores são os números que você pode multiplicar para obter outro número. Neste caso, estes são os fatores de 10, ou "d": 1, 2, 5 e 10. 
Comece usando o primeiro fator,1. substituto "1" para cada "X" na comparação:
(1) - 4(1) - 7(1) + 10 = 0 Isso dá: 1 - 4 - 7 + 10 = 0. Como 0 = 0 é uma afirmação verdadeira, você sabe que x = 1 é a solução. 
"x = 1" é o mesmo que "x - 1 = 0" ou "(x - 1)". Você só tem um "1" subtraído de cada lado da equação. 
Você pode fatorar (x - 1) de x? Não, isso não é possível. Mas se você primeiro emprestar um -x da segunda variável: x(x - 1) = x - x. Você pode fatorar (x - 1) do que resta da segunda variável? Não, isso não é possível aqui também. Você tem que pegar emprestado algo da terceira variável novamente, que é 3x de -7x. Isso nos dá -3x(x - 1) = -3x + 3x. Como você tirou 3x de -7x, a terceira variável agora é -10x e a constante é 10. Você pode desvincular isso. Sim claro! -10(x - 1) = -10x + 10. O que você fez foi reorganizar as variáveis para obter o fator (x - 1) de toda a equação. A equação modificada fica assim: x - x - 3x + 3x - 10x + 10 = 0, mas ainda é a mesma que x - 4x - 7x + 10 = 0. 
x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Você pode reorganizá-los para facilitar a dissolução novamente: (x - 1)(x - 3x - 10) = 0. Aqui você está apenas tentando fatorar (x - 3x - 10). Os fatores então se tornam (x + 2)(x - 5). 
(x - 1)(x + 2)(x - 5) = 0 Isso dá as soluções para 1, -2 e 5. Insira -2 na equação: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0. Insira 5 na equação: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Fatorando um polinômio de terceiro grau
Contente
Este artigo trata da fatoração de um polinômio cúbico, também chamado de polinômio. Vamos explorar como podemos fazer isso usando o agrupamento e os fatores do termo livre.
Degraus
Parte 1 de 2: Dissolver por agrupamento

1. Divida o polinômio em dois grupos. Dividir o polinômio ajuda a resolver cada parte individual.
- Suponha que estamos trabalhando com o seguinte polinômio:" x + 3x - 6x - 18 = 0. Vamos dividir isso em (x + 3x) e (-6x - 18)

2. Tente descobrir o que é o mesmo em cada grupo.

3. Remova esses fatores iguais dos dois termos.

4. Se cada um dos dois termos contiver o mesmo fator, você poderá combinar esses fatores.

5. Encontre a solução olhando para as raízes. Se você tiver x em uma raiz quadrada, lembre-se de que os números positivos e negativos são válidos para essa equação.
Parte 2 de 2: Fatorando com o termo livre

1. Reorganize a expressão da seguinte forma: ax+bx+cx+d.
- Suponha que você trabalhe com a equação: x - 4x - 7x + 10 = 0.

2. Encontre todos os fatores de "d". A constante "d" torna-se o número sem variáveis ao lado dele como "X".

3. Encontre um fator que torne o polinômio igual a zero. Queremos determinar qual fator torna o polinômio igual a zero se aplicarmos esse fator para "X" preencha a equação.
(1) - 4(1) - 7(1) + 10 = 0

4. Agora vá reorganizar tudo. Se x=1 então é possível escrever esta equação de forma ligeiramente diferente sem alterar o significado.

5. Fatore a raiz quadrada da equação. "(x - 1)" é a raiz. Tente fatorar isso do resto da equação. Faça isso com um polinômio de cada vez.

6. Prossiga para substituir os fatores do termo livre. Veja os números que você resolveu usando (x - 1) na Etapa 5:

7. Sua solução são as raízes fatoradas. Verifique esta solução inserindo cada um deles de volta na equação original.
Pontas
- A equação cúbica é o produto de 3 equações de primeiro grau ou de uma equação de primeiro grau e uma equação de segundo grau que não pode ser fatorada. No último caso, depois de encontrar o polinômio de primeiro grau, você usa a divisão longa para encontrar o polinômio de segundo grau.
- Não há polinômios cúbicos que não possam ser fatorados quando se trata de números reais, porque esta equação deve ter uma raiz quadrada de números reais. Equações de terceiro grau como x + x + 1 que têm uma raiz real irracional não podem ser fatoradas em polinômios com números inteiros ou racionais como coeficiente. Embora possa ser fatorado na própria equação, não pode ser reduzido a um polinômio inteiro.
Método 2 equivale a divisão longa de dois polinômios, um.v:
(x-1) ∕x³ - 4x²-7x+10 ∕
- x³ - 1x².................................= (x-1) (x²)
- - 3x²-7x
- 3x²+ 3x.........................= (x-1) (-3x)
- - 10x + 10
- 10x + 10................= (x-1) (-10)
- 0............................ x²- 3x-10 (quociente)
Os determinantes x², -3x e -10 do quociente são obtidos subtraindo-se sempre o 1º termo do divisor ( x ) do primeiro termo do dividendo, ou o que resta dele ( x³, -3x², -10x ).
Artigos sobre o tópico "Fatorando um polinômio de terceiro grau"
Оцените, пожалуйста статью
Popular