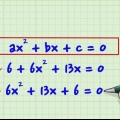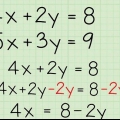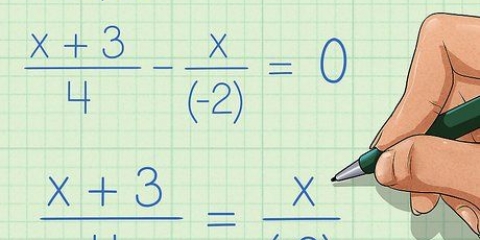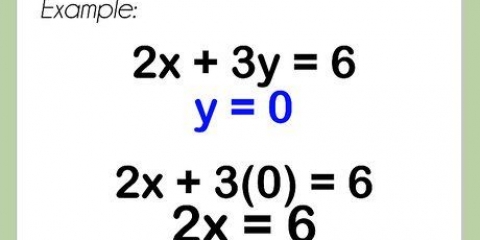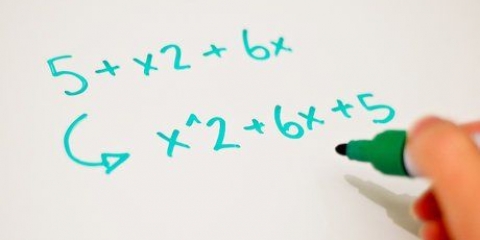Por exemplo, a variável 12y pode ser reescrita como o produto dos fatores de 12 e y. Podemos escrever 12y como 3(4y), 2(6y), etc., usando os fatores de 12 que são mais convenientes. Podemos até ir tão longe quanto 12 anos várias vezes dissolver. Em outras palavras, não precisamos parar em 3(4y) ou 2(6y) - podemos fatorar 4y e 6y em 3(2(2y) e 2(3(2y) respectivamente). Aparentemente essas duas expressões são equivalentes entre si. 
Vamos tentar um problema de exemplo. Para fatorar a equação 12x + 6, primeiro procuramos o mdc de 12x e 6. 6 é o maior número que divide 12x e 6, então podemos simplificar a equação para 6(2x + 1). Este processo também se aplica a equações envolvendo números negativos e frações. x/2 + 4, por exemplo, pode ser simplificado para 1/2(x + 8) e -7x + -21 pode ser fatorado em -7(x + 3). 

Por exemplo, pegue a equação quadrática x + 5x + 6 = 0. Como 3 x 2 = 6 e 3 + 2 = 5, a equação simplificada se torna (x + 3)(x + 2). Pequenas variações nesta solução rápida simples podem ser encontradas na própria equação: Se a equação quadrática estiver na forma x-bx+c, sua resposta ficará assim: (x - _)(x - _). Se estiver na forma x+bx+c, sua resposta ficará assim: (x + _)(x + _). Se estiver na forma x-bx-c, sua resposta ficará assim: (x + _)(x - _). Nota: Os espaços em branco podem ser frações ou decimais. Por exemplo, a equação x + (21/2)x + 5 = 0 fatores em (x + 10)(x + 1/2). 
Vamos fazer uma tarefa de exemplo. 3x - 8x + 4 parece um pouco intimidante no começo. Mas se percebermos que 3 tem apenas dois fatores (3 e 1), fica muito mais fácil, pois sabemos que nossa resposta deve ser da forma (3x +/- _)(x +/- _). Nesse caso, inserir -2 nos espaços em branco dará a resposta correta. -2 × 3x = -6x e -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, então vemos que os termos fatorados entre parênteses multiplicados, têm a equação original como o produto. 
Por exemplo, a equação x + 6x + 9 satisfaz esta forma. 3 é 9 e 3 × 2 é 6. Então sabemos que os fatores desta equação são iguais a (x + 3)(x + 3) ou (x + 3). 
Vamos voltar para a equação x + 5x + 6 = 0. A equação resolvida é (x + 3)(x + 2) = 0. Se um desses fatores for igual a 0, então a equação inteira é 0, então as respostas possíveis para x são aqueles números onde (x + 3) e (x + 2) são iguais a 0. Esses números são -3 e -2, respectivamente. 
Aplicamos -2 e -3 a x + 5x + 6 = 0. Primeiro: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Isso está correto, então -2 é uma resposta válida. Agora tentamos -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Isso também está correto, então -3 também é uma resposta válida. 

A equação 4x + 8xy + 4y pode ser reescrita como 4x + (2 × 2 × 2)xy + 4y. Agora fica claro que está na forma correta, de modo que podemos afirmar com alguma confiança que nossa equação pode ser fatorada em (2x + 2y). 
Por exemplo: 8x - 27y pode ser fatorado em (2x - 3y)(4x + ((2x)(3y)) + 9y).
Equações de fatoração
Contente
Em matemática é fatorar determinar números ou expressões que, quando multiplicados, produzem um determinado valor ou equação. A fatoração é uma habilidade útil para aprender ao resolver problemas matemáticos simples; a capacidade de fatorar corretamente torna-se quase essencial ao lidar com equações quadráticas e outros polinômios. A fatoração pode ser usada para simplificar equações matemáticas simples para resolvê-las mais facilmente. A fatoração pode permitir que você mesmo exclua possíveis respostas muito mais rápido do que se tivesse que verificar cada uma delas.
Degraus
Método 1 de 3: fatoração de números e equações simples

1. Entenda a definição de fatoração em números. A fatoração é simples em princípio, mas na prática pode ser bastante desafiadora ao resolver equações complexas. Portanto, a abordagem mais simples é começar com números pequenos e depois equações simples antes de passar para aplicações mais avançadas. O fatores de um determinado número são os números que, multiplicados entre si, produzem esse único número. Por exemplo, os fatores de 12 são 1, 12, 2, 6, 3 e 4, porque 1 × 12, 2 × 6 e 3 × 4 têm 12 como produto.
- Outra maneira de pensar nisso é que os fatores de um determinado número são aqueles números que fazem o número em pode ser compartilhado em sua totalidade.
- Você pode encontrar todos os fatores de 60? Usamos o número 60 para várias aplicações (o número de minutos em uma hora, segundos em um minuto, etc.).) porque é divisível por um grande conjunto de números.
- Os fatores de 60 são 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60.

2. Entenda que as equações também podem ser fatoradas. Assim como os números, variáveis com coeficientes também podem ser fatoradas. Você faz isso encontrando os fatores do coeficiente da variável. Saber como fatorar variáveis é útil para simplificar as equações das quais as variáveis fazem parte.

3. Aplicar a propriedade distributiva da multiplicação para fatorar equações matemáticas. Usando seu conhecimento de como fatorar números regulares e variáveis com coeficientes, você também pode simplificar equações matemáticas determinando os fatores comuns a números e variáveis em uma equação matemática. Normalmente, simplificaremos a equação o máximo possível, procurando o máximo divisor comum (mcd). Este processo de simplificação é possível devido à propriedade distributiva da multiplicação, que afirma que para qualquer número a, b e c, a(b + c) = ab + ac.
Método 2 de 3: fatoração de equações quadráticas

1. Verifique se a equação está na forma quadrática (ax + bx + c = 0). equações quadráticas são da forma ax + bx + c = 0, onde a, b e c são constantes numéricas e a não é igual a 0 (note que a é igual a posso estão em 1 ou -1). Se você está lidando com uma equação com uma variável (x) e um ou mais termos de x ao quadrado, normalmente você pode trocar os termos da equação usando uma operação matemática padrão para obter 0 em um lado da equação. sinal e machado, etc. por outro lado.
- Por exemplo, você tem a seguinte equação matemática: 5x + 7x - 9 = 4x + x - 18 que pode ser simplificada para x + 6x + 9 = 0, na forma quadrática.
- Equações com potências maiores de x, como x, x, etc. não são equações do segundo grau. Estas são equações cúbicas ou superiores, a menos que a equação possa ser simplificada para que os termos com maiores potências de x (que quadrados) sejam eliminados.

2. Em equações quadráticas onde a = 1, você fatora em (x+d )(x+e), onde d × e = ce d + e = b. Se sua equação quadrática estiver na forma x + bx + c = 0 (em outras palavras, se o coeficiente de x = 1), então é possível (mas não certo) que um atalho relativamente simples possa ser usado para fatorar a equação. Encontre dois números que tenham c como produto e some-os para obter b como uma soma. Se você tiver esses dois números d e e, coloque-os na seguinte expressão: (x+d)(x+e). Esses dois termos, quando multiplicados, dão a você a equação quadrática - em outras palavras, eles são os fatores da sua equação quadrática.

3. Se possível, você também pode dissolver os fatores apenas olhando de perto. Acredite ou não, você pode resolver equações quadráticas simples apenas observando o problema com cuidado e depois pesando as respostas possíveis até encontrar a correta. Em outras palavras, decomponha-se em fatores experimentando. Se a equação é da forma ax+bx+c e a>1, então os termos serão da forma (dx +/- _)(ex +/- _), onde d e e são constantes, maiores que zero, que multiplicadas têm a como produto. Ambos d e e (ou ambos) posso igual a 1, mas nem sempre é assim. Se ambos forem 1, você basicamente usou o método rápido descrito acima.

4. Resolva isso ao quadrado. Em alguns casos, equações quadráticas podem ser fatoradas rápida e facilmente usando uma propriedade matemática especial. Qualquer equação quadrática da forma x + 2xh + h = (x + h). Então, se em sua equação o valor de b é o dobro da raiz quadrada de c, então sua equação pode ser fatorada em (x + (sqrt(c))).

5. Use fatores para resolver equações do segundo grau. Independentemente de como você fatora uma equação quadrática; uma vez que é fatorado, você pode encontrar as respostas possíveis para o valor de x definindo cada fator igual a zero e resolvendo para ele. Como você está procurando valores para x onde sua equação é zero, um valor para x que torne qualquer fator igual a zero será a resposta possível da sua equação quadrática.

6. Verifique suas respostas – algumas delas podem estar incorretas! Depois de encontrar as respostas possíveis para x, aplique-as de volta à sua equação original para ver se elas são válidas. Às vezes, as respostas que você encontra serão a equação original não igualar a zero ao aplicá-los. Essas respostas são incorreta e nós os ignoramos.
Método 3 de 3: Fatorando outras formas de equações

1. Se a equação é da forma a-b, então os termos fatorados são (a+b)(a-b). As equações de duas variáveis são resolvidas de forma diferente das equações quadráticas. Para qualquer equação a-b onde a e b não são iguais a 0, os fatores da equação são (a+b)(a-b).
- Por exemplo, a equação 9x - 4y = (3x + 2y)(3x - 2y).

2. Se a equação é da forma a+2ab+b, decomponha-a em (a+b). Nota: com a o trinômio da forma a-2ab+b, a forma dissolvida é ligeiramente diferente: (a-b).

3. Se a equação é da forma a-b, então você a decompõe em (a-b)(a+ab+b). Finalmente, deve-se mencionar que equações cúbicas e polinômios superiores também podem ser fatorados, embora esse processo rapidamente se torne inviável e complicado.
Pontas
- a-b pode ser fatorado, mas a+b não.
- Aprenda a fatorar constantes – isso pode ajudar.
- Cuidado com as frações durante a fatoração e calcule-as corretamente e com cuidado.
- Se você tem um trinômio da forma x+bx+ (b/2), então a forma fatorada é (x+(b/2)) (você pode encontrar isso com uma fórmula quadrada).
- Lembre-se que x 0 = 0.
Necessidades
- Papel
- Lápis
- Livro de matemática (se necessário)
Artigos sobre o tópico "Equações de fatoração"
Оцените, пожалуйста статью
Popular