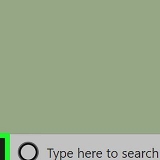
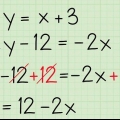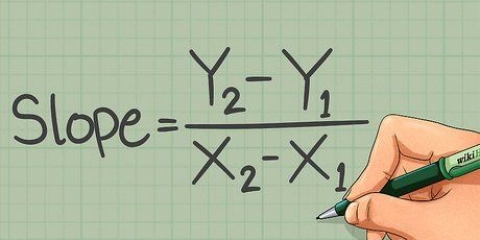4x = 8 - 2a (4x)/4 = (8/4) - (2a/4) x = 2 - y 
Agora você sabe que: x = 2 - y. A segunda equação, que você ainda não alterou, é: 5x + 3x = 9. Na segunda equação, substitua x por `2 - ½y`: 5(2 - ½ ano) + 3 anos = 9. 
5(2 - ½ ano) + 3 anos = 9 10 – (5/2)a + 3a = 9 10 – (5/2)a + (6/2)a = 9 (Se você não entender esta etapa, aprenda como somar frações. Isso é frequentemente, mas nem sempre, necessário com este método). 10 + y = 9 y = -1 y = -2 
Agora você sabe que: y = -2 Uma das equações originais é: 4x + 2a = 8. (Ambas as equações podem ser usadas para esta etapa). Conecte -2 em vez de y: 4x + 2(-2) = 8. 4x - 4 = 8 4x = 12 x = 3 
Se você terminar com uma equação sem variáveis e que não é verdadeira (por exemplo, 3 = 5), então o problema tem sem solução. (Se você tiver representado graficamente as equações, verá que elas são paralelas e nunca se cruzam). Se você terminar com uma equação sem variáveis, mas aquelas Nós vamos é verdadeiro (por exemplo, 3 = 3), então o problema tem um número infinito de soluções. As duas equações são exatamente iguais entre si. (Se você representar graficamente as duas equações, verá que elas se sobrepõem exatamente). 

Suponha que você tenha o sistema de equações 3x - y = 3 e -x + 2y = 4. Vamos modificar a primeira equação para que a variável y está sendo eliminado. (Você também pode fazer isso para X fazer e obter a mesma resposta). O - você da primeira equação deve ser eliminada com o+ 2 anos ` na segunda equação. Podemos fazer isso por - y multiplicar por 2. Multiplicamos ambos os lados da primeira equação por 2, como segue: 2(3x - y)=2(3), e assim 6x - 2a = 6. Agora vai - 2 anos cair contra o +2 anos na segunda equação. 
Suas equações são: 6x - 2a = 6 e -x + 2y = 4. Combine os lados esquerdos: 6x - 2y - x + 2y = ? Combine os lados certos: 6x - 2y - x + 2y = 6 + 4. 
Você tem: 6x - 2y - x + 2y = 6 + 4. Agrupe as variáveis X e y um com o outro: 6x - x - 2y + 2y = 6 + 4. Simplificar: 5x = 10 Resolva para x: (5x)/5 = 10/5, de modo a x = 2. 
Você sabe disso x = 2, e que uma de suas equações originais 3x - y = 3 é. Conecte 2, em vez de x: 3(2) - y = 3. Resolva para y na equação: 6 - y = 3 6 - y + y = 3 + y, assim 6 = 3 + y 3 = y 
Se sua equação combinada não tiver variáveis e não for verdadeira (como 2 = 7), então não há sem solução que vale para ambas as equações. (Se você representar graficamente ambas as equações, verá que elas são paralelas e nunca se cruzam). Se sua equação combinada não tem variáveis e é verdadeira (como 0 = 0), então existem um número infinito de soluções. As duas equações são realmente idênticas. (Se você colocá-los em um gráfico, verá que eles se sobrepõem completamente). 

A primeira equação é: 2x + y = 5. Altere isso para: y = -2x + 5. A segunda equação é: -3x + 6a = 0. Altere isso para 6a = 3x + 0, e simplificar paray = ½ x + 0. As duas equações são idênticas, então toda a linha se torna uma `interseção`. Escrever: soluções infinitas. 
Se você não tiver papel milimetrado, use uma régua para garantir que os números estejam espaçados uniformemente. Se você estiver usando números grandes ou decimais, talvez seja necessário dimensionar o gráfico. (Por exemplo 10, 20, 30 ou 0.1, 0.2,0.3 em vez de 1, 2, 3). 
Nos exemplos acima mencionados, uma linha (y = -2x + 5) no eixo y 5. A outra linha (y = ½ x + 0) passa pelo ponto zero 0. (Estes são os pontos (0,5) e (0,0) no gráfico). Marque cada uma das linhas com uma cor diferente, se possível. 
No nosso exemplo, a regra y = -2x + 5 uma inclinação de -2. Em x = 1, a linha cai 2 baixado ponto x = 0. Desenhe o segmento de linha entre (0,5) e (1,3). A regra y = ½ x + 0tem uma inclinação de ½. Em x = 1, a linha vai ½ acima do ponto x = 0. Desenhe o segmento de linha entre (0,0) e (1,½). Se as linhas têm a mesma inclinação as linhas nunca se cruzarão, então não há solução para o sistema de equações. Escrever: sem solução. 
Se as linhas estiverem se movendo uma em direção à outra, você continuará desenhando pontos nessa direção. Se as linhas se afastarem uma da outra, volte e desenhe pontos na outra direção, começando em x = -1. Se as linhas não estiverem próximas umas das outras, pule em frente e trace pontos mais distantes, como x = 10. 
Resolvendo sistemas de equações com duas variáveis
Contente
Em um `sistema de equações` você é solicitado a resolver duas ou mais equações ao mesmo tempo. Quando esses dois contêm variáveis diferentes, como x e y, ou a e b, pode ser difícil, à primeira vista, ver como resolvê-los. Felizmente, uma vez que você sabe o que fazer, você só precisa de algumas habilidades matemáticas básicas (e às vezes algum conhecimento de frações) para resolver o problema. Se for necessário, ou se você é um aprendiz visual, aprenda também a representar graficamente as equações. Desenhar (traçar) um gráfico pode ser útil para `ver o que está acontecendo` ou para verificar seu trabalho, mas também pode ser mais lento do que os outros métodos e não funciona com todos os sistemas de equações.
Degraus
Método 1 de 3: usando o método de substituição

1. Mova as variáveis para diferentes lados da equação. Este método de `substituição` começa por `resolver x` (ou qualquer outra variável) em uma das equações. Por exemplo, temos as seguintes equações: 4x + 2a = 8 e 5x + 3x = 9. Primeiro, vamos olhar para a primeira equação. Reorganize subtraindo 2y de cada lado e você obtém: 4x = 8 - 2a.
- Este método geralmente usa frações em um estágio posterior. Você também pode usar o método de eliminação abaixo, se preferir não trabalhar com frações.

2. Divida ambos os lados da equação para `resolver para x`. Depois de ter o termo x (ou qualquer variável que você use) em um lado da equação, divida os dois lados da equação para isolar a variável. Por exemplo:

3. Conecte isso de volta à outra equação. Certifique-se de retornar ao Outras comparação, não a que você já usou. Nessa equação, você substitui a variável que resolveu de modo que resta apenas uma variável. Por exemplo:

4. Resolva para a variável restante. Agora você tem uma equação com apenas uma variável. Use técnicas comuns de álgebra para resolver essa variável. Se as variáveis se cancelarem, vá para a última etapa. Caso contrário, você terá uma resposta para uma de suas variáveis:

5. Use a resposta para resolver a outra variável. Não cometa o erro de terminar o problema pela metade. Você precisará reinserir a resposta obtida em uma das equações originais para poder resolver a outra variável:

6. Saiba o que fazer quando ambas as variáveis se cancelam. Quando você x = 3y + 2 ou obtém uma resposta semelhante na outra equação, então você tenta obter uma equação com apenas uma variável. Às vezes você acaba com uma equação em vez disso sem variáveis. Verifique seu trabalho e certifique-se de substituir a primeira equação (reorganizada) na segunda equação, não na primeira equação. Quando tiver certeza de que não cometeu nenhum erro, você obterá um dos seguintes resultados:
Método 2 de 3: Usando o método de eliminação
1. Determina a variável a ser eliminada. Às vezes, as equações `eliminam` umas às outras em uma variável assim que você as adiciona. Por exemplo, quando você faz as equações 3x + 2a = 11 e 5x - 2a = 13 combina, o `+2y` e o `-2y` se eliminarão, com todos os `ys são removidos da equação. Veja as equações do seu problema para descobrir se alguma das variáveis será eliminada desta forma. Se nenhuma das variáveis for eliminada, leia a próxima etapa para obter conselhos.


2. Multiplicar uma equação para eliminar uma variável. (Pule esta etapa se as variáveis já se eliminaram). Se nenhuma das variáveis nas equações for eliminada por si só, você precisará modificar uma das equações para que elas. Isso é mais fácil de entender com um exemplo:

3. Combine as duas equações. Para combinar duas equações, some os lados esquerdo e direito. Se você escreveu a equação corretamente, uma das variáveis deve se cancelar em relação à outra. Aqui está um exemplo usando as mesmas equações da última etapa:

4. Resolva a última variável. Simplifique a equação combinada e use a álgebra básica para resolver a última variável. Se não houver mais variáveis após a simplificação, pule para a última etapa desta seção. Caso contrário, você deve acabar com uma resposta simples para uma de suas variáveis. Por exemplo:

5. Resolva as outras variáveis. Você encontrou uma variável, mas ainda não terminou. Substitua sua resposta em uma das equações originais para que você possa resolver a outra variável. Por exemplo:

6. Saiba o que fazer se ambas as variáveis se cancelarem. Às vezes, combinar duas equações resulta em uma equação que não faz sentido ou não ajuda a resolver o problema. Verifique seu trabalho desde o início, mas se você não cometeu um erro, escreva uma das seguintes respostas:
Método 3 de 3: Representando graficamente as equações

1. Use este método somente quando especificado. A menos que você esteja usando um computador ou uma calculadora gráfica, muitos sistemas de equações só podem ser resolvidos aproximadamente usando esse método. Seu professor ou livro de matemática pode pedir para você usar esse método, então você provavelmente está familiarizado com equações gráficas como linhas. Você também pode usar este método para verificar se suas respostas de um dos outros métodos estão corretas.
- A ideia básica é que você faça o gráfico de ambas as equações e determine o ponto onde elas se cruzam. Os valores de x e y neste ponto rendem o valor de x e o valor de y no sistema de equações.

2. Resolva as duas equações para y. Mantendo as duas equações separadas, use álgebra para converter cada equação na forma `y = __x + __`. Por exemplo:

3. Desenhe um sistema de coordenadas. Em um pedaço de papel quadriculado, desenhe um `eixo y` vertical e um `eixo x` horizontal. Comece no ponto em que as linhas se cruzam e rotule os números 1, 2, 3, 4, etc. para cima ao longo do eixo y e novamente à direita ao longo do eixo x. Rotule os números -1, -2, etc. para baixo no eixo y e para a esquerda ao longo do eixo x.

4. Desenhe a interseção y para cada linha. Uma vez que você tenha uma equação na forma y = __x + __ você pode começar a grafá-lo, desenhando um ponto onde a linha intercepta o eixo y. Isso está sempre em um valor y, igual ao último número nesta equação.

5. Use a inclinação para continuar desenhando as linhas. Na forma y = __x + __, é o número para o x de declive fora da linha. Cada vez que x é aumentado em um, o valor de y aumentará pelo valor da inclinação. Use esta informação para encontrar o ponto no gráfico para cada linha, quando x = 1. (Alternativamente, substitua x = 1 para qualquer equação e resolva para y).

6. Continue traçando as linhas até que elas se cruzem. Pare e olhe para o seu gráfico. Se as linhas já se cruzaram, continue para a próxima etapa. Caso contrário, você toma uma decisão com base no que as linhas fazem:

7. Encontre a resposta na intersecção das linhas. Uma vez que as duas linhas se cruzam, os valores x e y nesse ponto são a solução para o problema. Se você tiver sorte, a resposta será um número inteiro. Por exemplo, em nossos exemplos, as duas linhas se cruzam (2.1) assim é a sua resposta x = 2 e y = 1. Em alguns sistemas de equações, as linhas se cruzarão em um valor entre dois inteiros e, a menos que seu gráfico seja extremamente preciso, será difícil dizer onde ele está. Se este for o caso, você pode dar uma resposta como: `x está entre 1 e 2`. Você também pode usar o método de substituição ou o método de eliminação para encontrar a resposta exata.
Pontas
- Você pode verificar seu trabalho alimentando as respostas de volta nas equações originais. Se as equações forem verdadeiras (por exemplo, 3 = 3), sua resposta está correta.
- No método de eliminação, às vezes você tem que multiplicar uma equação por um número negativo para eliminar uma variável.
Avisos
- Esses métodos não podem ser usados ao lidar com um número de potência, como x. Para mais informações sobre equações deste tipo você precisa de um guia para fatorar quadrados com duas variáveis.
Artigos sobre o tópico "Resolvendo sistemas de equações com duas variáveis"
Оцените, пожалуйста статью
Popular