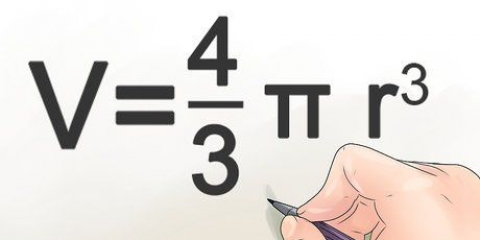bol: onde r é o raio da esfera.
onde r é o raio da esfera. Cone: onde r é o raio da base circular e h é a altura do cone.
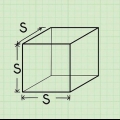
onde r é o raio da base circular e h é a altura do cone. Cubo:  onde s é o comprimento de um lado.
onde s é o comprimento de um lado. Prisma Retângular:  onde l é o comprimento de um lado de uma face retangular, w é a largura de uma face retangular e h é a altura do prisma.
onde l é o comprimento de um lado de uma face retangular, w é a largura de uma face retangular e h é a altura do prisma. Cilindro:  onde r é o raio da base circular e h é a altura do cone.
onde r é o raio da base circular e h é a altura do cone. Pirâmide:  onde B é a área da base da pirâmide e h é a altura da pirâmide.
onde B é a área da base da pirâmide e h é a altura da pirâmide. 
O raio de um círculo é metade do seu diâmetro. Meça o diâmetro com uma régua pelo centro do círculo e leia a leitura. Calcule o raio dividindo o diâmetro por dois. Determinar o raio de uma esfera requer um pouco mais de esforço, mas pode ser feito de várias maneiras, como mostra a figura Este artigo. O comprimento, a largura e a altura dos objetos podem ser medidos com uma régua, medindo de uma extremidade de um objeto à outra. 
Não se esqueça de dar sua resposta em unidades cúbicas. Se você usa métricas ou SIs, a unidade de volume é sempre cúbica. Sempre adicione unidades no final do seu cálculo. 

Ao medir o volume inicial de água, observe o nível do líquido ao nível dos olhos e observe a leitura na parte inferior do menisco. O menisco é a curva que a água faz quando entra em contato com uma superfície. 
Se você derramou água ao colocar o objeto no copo, tente novamente com um copo medidor maior ou use menos água. 
Por exemplo, suponha que você começou com 35 ml de água e terminou com 65 ml de água; o volume do seu objeto é então 65 – 35 = 30 ml ou 30 cm 


Por exemplo, calcule a densidade  de uma substância com um volume de 8 cm e uma massa de 24 g.
de uma substância com um volume de 8 cm e uma massa de 24 g. 
Calcular volume e densidade
Contente
Volume é a quantidade de espaço que um objeto ocupa enquanto densidade é a massa do objeto por unidade de volume. Você deve primeiro saber o volume de um objeto antes de poder calcular sua densidade. Você pode calcular o volume de objetos regulares com uma fórmula simples, determinada pela forma do objeto. As unidades comumente usadas para volume são os centímetros cúbicos (cm) e metros cúbicos (m). Depois de calcular o volume, a densidade é determinada com um cálculo simples. As unidades comumente usadas para densidade são gramas por centímetro cúbico (g/cm) ou gramas por mililitro (g/mL).
Degraus
Parte 1 de 3: Calculando o volume de um objeto regular

1. Determine a forma do objeto. Ao conhecer a forma de um objeto, você pode determinar a fórmula correta e fazer os cálculos necessários para o volume.
- UMA esfera é um objeto tridimensional perfeitamente redondo, onde cada ponto em sua superfície é equidistante do centro. Em outras palavras, uma esfera é um objeto esférico.
- UMA cone é um objeto tridimensional com uma base circular e um ponto. Outra maneira de pensar nisso é que um cone é um tipo especial de pirâmide com uma base circular.
- UMA cubo é uma forma tridimensional com seis faces quadradas idênticas.
- UMA paralelepípedo, também chamado de prisma retangular, parece um cubo, pois é uma forma tridimensional com seis lados, mas neste caso os lados são retangulares em vez de quadrados.
- UMA cilindro é uma forma tridimensional com dois círculos planos idênticos e uma única superfície plana curvada conectando os dois círculos.
- UMA pirâmide é uma forma tridimensional com um polígono como base e lados inclinados que se encontram em um ponto (a ponta da pirâmide).Uma pirâmide regular é uma pirâmide com um polígono regular como base da pirâmide, o que significa que todos os lados do polígono são iguais em comprimento e todos os ângulos são iguais em tamanho.
- Se o seu objeto tiver uma forma irregular, você pode usar o método de deslocamento para determinar seu volume.

2. Escolha a equação correta para calcular o volume. Cada forma tem sua própria fórmula para calcular quanto espaço tridimensional ela ocupa. Abaixo você encontrará as fórmulas para os objetos mencionados anteriormente. Leia mais sobre isso calculando o volume para exemplos e imagens mais detalhados dessas fórmulas.
 onde r é o raio da esfera.
onde r é o raio da esfera. onde r é o raio da base circular e h é a altura do cone.
onde r é o raio da base circular e h é a altura do cone. onde s é o comprimento de um lado.
onde s é o comprimento de um lado. onde l é o comprimento de um lado de uma face retangular, w é a largura de uma face retangular e h é a altura do prisma.
onde l é o comprimento de um lado de uma face retangular, w é a largura de uma face retangular e h é a altura do prisma. onde r é o raio da base circular e h é a altura do cone.
onde r é o raio da base circular e h é a altura do cone. onde B é a área da base da pirâmide e h é a altura da pirâmide.
onde B é a área da base da pirâmide e h é a altura da pirâmide.
3. Faça as medidas necessárias. As medidas que você precisa são determinadas pela forma do objeto. Para a maioria dos objetos, você precisa da altura, mas o raio é suficiente se a forma for circular ou o comprimento e a largura de objetos com faces retangulares.

4. Calcule o volume. Agora que você determinou a forma, sabe qual fórmula usar e fez as medidas necessárias, pode calcular o volume. Insira suas leituras e faça os cálculos necessários. O produto final é o volume do seu objeto.
Parte 2 de 3: Calcule o volume de um objeto irregular

1. Calcule o volume do objeto usando o deslocamento. Pode ser difícil determinar as dimensões de objetos de formato irregular, o que posteriormente levará a medições incorretas e cálculos de volume. Ao medir quanta água é deslocada por um objeto, você pode calcular seu volume sem fórmulas complexas.
- Este método também pode ser usado para calcular o volume de uma forma regular.

2. Encha um cilindro graduado com água. Um cilindro graduado é um instrumento de laboratório com marcações na parte externa e permite medir o volume de uma certa quantidade de líquido. Certifique-se de que o cilindro graduado é grande o suficiente para segurar o objeto. Encha-o com água suficiente para que o objeto fique completamente submerso, mas a água não derrame pela borda. Observe o nível inicial da água.

3. Coloque o objeto calmamente no copo. Tenha cuidado para não deixar cair o objeto na água, caso contrário a água pode escorrer pela borda e a leitura será incorreta. Certifique-se de que o objeto esteja completamente submerso na água. Observe o novo nível de água do copo, novamente ao nível dos olhos, prestando muita atenção ao menisco.

4. Subtraia o novo nível de água do nível inicial. A quantidade de água deslocada pelo objeto é igual ao volume do objeto medido em centímetros cúbicos. Líquidos são geralmente medidos em mililitros, e um mililitro é igual a um centímetro cúbico.
Parte 3 de 3: Calculando a densidade

1. Determine a massa do objeto. A quantidade de matéria em um objeto é a massa desse objeto. Isso pode ser medido diretamente colocando o objeto em uma balança com a unidade em gramas.
- Tenha uma balança precisa à mão e coloque o objeto sobre ela. Anote sua massa em seu caderno.
- Você também pode medir a massa com uma balança. Com o objeto de um lado, coloque pesos de massa conhecida do outro lado da balança até que estejam em equilíbrio com o objeto. A massa do seu objeto é igual à massa total dos pesos.
- É importante certificar-se de que seu item está seco antes de pesá-lo. Dessa forma, você tem a certeza de que o resultado da medição não é menos preciso devido à água absorvida.

2. Calcule o volume do seu objeto. Se o seu objeto tiver uma forma regular, calcule o volume usando um dos métodos indicados anteriormente. Se a forma for irregular, calcule o volume usando o método de deslocamento conforme explicado acima.

3. Calcule a densidade. A densidade é definida como a massa dividida pelo volume. Finalmente, para determinar a densidade, divida a massa ponderada pelo volume medido. O resultado é a densidade do metal expressa em g/cm.
 de uma substância com um volume de 8 cm e uma massa de 24 g.
de uma substância com um volume de 8 cm e uma massa de 24 g.
Pontas
- Você pode testar seus cálculos de volume comparando o resultado do método de deslocamento e os cálculos.
- Os objetos geralmente são uma montagem de vários objetos geométricos, então você pode dividi-los em grupos básicos menores para determinar o volume de cada um e, em seguida, somá-los todos juntos para determinar o volume do objeto.
Avisos
- Certifique-se de ter todas as medidas em unidades métricas ou SI antes de prosseguir com seus cálculos.
Artigos sobre o tópico "Calcular volume e densidade"
Оцените, пожалуйста статью
Popular