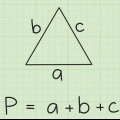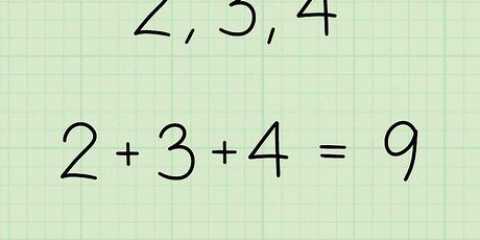Determinando o Terceiro Ângulo de um Triângulo

Contente

Degraus
Avisos

Determinar o terceiro ângulo de um triângulo se você souber quais são os outros dois ângulos é fácil. Tudo o que você precisa fazer é subtrair os outros ângulos de 180° para encontrar o terceiro ângulo. No entanto, existem algumas outras maneiras de determinar o terceiro ângulo de um triângulo, dependendo do problema com o qual você está trabalhando. Se você quiser aprender a determinar esse ilustre terceiro canto de um triângulo, leia o Passo 1 para começar.

Degraus

Método 1 de 3: Usando os outros dois cantos

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 1

1. Some os dois ângulos conhecidos. Tudo que você precisa saber é que todos os ângulos de um triângulo somam sempre ser 180°. Isso é sempre verdade. Então, se você conhece dois dos três cantos do triângulo, está faltando apenas uma pequena peça do quebra-cabeça. A primeira coisa que você pode fazer é somar os ângulos que você já conhece. Neste exemplo, os ângulos que você conhece são 80° e 65°. Adicione-os (80° + 65°) para obter 145°.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 2

2. Subtraia este número de 180°. Os ângulos de um triângulo são somados 180°. Portanto devo o ângulo restante junto com os outros ângulos são 180°. Neste exemplo: 180° - 145° = 35°.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 3

3. Anote sua resposta. Agora você sabe que o terceiro ângulo é 35°. Em caso de dúvida, basta verificar o seu trabalho. Os três ângulos juntos devem ser 180 graus, caso contrário não é um triângulo. 80° + 65° + 35° = 180°. Agora você está pronto.

Método 2 de 3: usando variáveis

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 4

1. Anote o problema. Às vezes você não tem tanta sorte e não sabe os valores dos dois ângulos de um triângulo, mas só tem algumas variáveis, ou algumas variáveis e um ângulo. Digamos que você esteja lidando com o seguinte problema: Determine o ângulo `x` do triângulo com dimensões `x`, `2x` e 24°. Apenas escreva isso primeiro.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 5

2. Adicione todas as dimensões juntas. É o mesmo princípio que você seguiria se conhecesse os dois ângulos. Basta combinar os valores dos ângulos combinando as variáveis. assim, x + 2x + 24° = 3x + 24°.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 6

3. Subtraia esses valores de 180°. Em seguida, subtraia esses valores de 180° para chegar mais perto de resolver o problema. Verifique se a equação é igual a 0. Isto é o que isto parece:

180° - (3x + 24°) = 0

180° - 3x - 24° = 0

156° - 3x = 0

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 7

4. Agora resolva para x. Agora mova as variáveis para um lado da equação e os números para o outro lado. Você obtém 156° = 3x. Agora divida ambos os lados da equação por 3 para obter x = 52°. Isso significa que o terceiro ângulo do triângulo deve ser de 52°. O outro ângulo é 2x (2x 52° ou 104°).

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 8

5. Verifique seu trabalho. Se você quiser ter certeza de que este é um triângulo válido, basta somar os três valores dos ângulos para ver se eles somam 180°. Isso é 52° + 104° + 24° = 180°. Agora você está pronto.

Método 3 de 3: usando outros métodos

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 9

1. Encontre o terceiro ângulo de um triângulo isósceles. Triângulos isósceles têm dois lados iguais e dois ângulos iguais. Os lados iguais são marcados com um sinal de hash, o que indica que os ângulos opostos a ambos os lados são iguais. Se você conhece a medida angular de um ângulo igual de um triângulo isósceles, então também conhece o outro ângulo igual. Você pode determinar isso da seguinte forma:

Se um dos ângulos iguais é 40°, então você sabe que o outro ângulo também é 40°. Você pode encontrar o terceiro lado, se necessário, subtraindo 40° + 40° (que é 80°) de 180°. 180° - 80° = 100°, que é o ângulo restante.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 10

2. Encontre o terceiro ângulo de um triângulo equilátero. Um triângulo equilátero tem apenas lados iguais e ângulos iguais. Muitas vezes isso é indicado por duas marcas de hash no meio de cada um dos lados. Isso significa que o valor de qualquer ângulo em um triângulo equilátero é 60°. Verifique seu trabalho. 60° + 60° + 60° = 180°.

Imagem intitulada Encontre o terceiro ângulo de um triângulo Passo 11

3. Encontre o terceiro ângulo de um triângulo retângulo. Suponha que você tenha um triângulo retângulo, cujos outros ângulos são 30°. Se for um triângulo retângulo, então você sabe que um dos ângulos é exatamente 90°. Os mesmos princípios se aplicam. Tudo o que você precisa fazer é somar os ângulos que conhece (30° + 90° = 120°) e subtrair esse número de 180°. De fato, 180° - 120° = 60°. Então o terceiro ângulo é 60°.

Avisos

Cometer um erro ao adicionar e subtrair devem resultar em uma resposta errada. É sempre uma boa ideia verificar o seu trabalho, mesmo que não pareça estar errado.