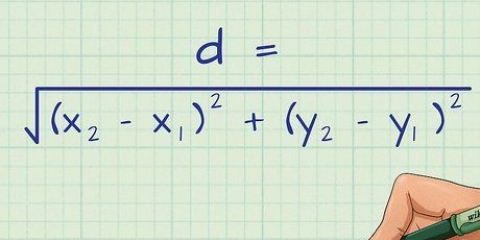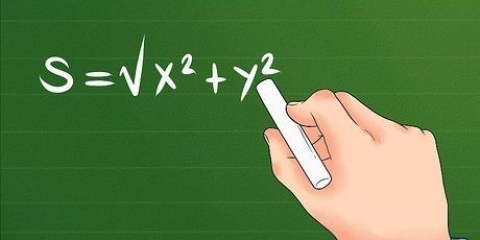Use as informações fornecidas no problema para fazer um desenho da prova. Nomeie os conhecidos e estranhos. Ao elaborar a evidência, use as informações necessárias para apoiar a evidência. 
Você percebe que uma prova é apenas um bom argumento onde cada passo é fundamentado. Você pode encontrar muitas evidências para estudar on-line e em um livro didático. 
Consulte seu professor após a aula para obter explicações adicionais. 

Conhecer seu público ajudará você a articular as evidências de uma maneira que ele entenderá, dada a quantidade de conhecimento prévio que o público possui. 
Uma prova de duas colunas é uma estrutura em que os dados e as declarações são colocados em uma coluna e as evidências de apoio ao lado em uma segunda coluna. Eles são muito comumente usados em geometria. Uma prova informal em parágrafos usa declarações gramaticalmente corretas e menos símbolos. Em um nível mais alto, você deve sempre usar provas informais. 
Por exemplo: Ângulo A e ângulo B formam um par linear. Dado. O ângulo ABC é reto. Definição de ângulo reto. Ângulo ABC é 180°. Definição de uma linha. Ângulo A + ângulo B = ângulo ABC. Postulado para adicionar ângulos. Ângulo A + ângulo B = 180°. substituição. Ângulo A como complemento do ângulo B. Definição de Ângulos Adicionais. Q.E.d. 
Por exemplo: suponha que os ângulos A e B sejam pares lineares. A hipótese é que o ângulo A e o ângulo B se complementam (são suplementares). O ângulo A e o ângulo B formam uma linha reta porque são pares lineares. Uma linha reta é definida como tendo um ângulo de 180°. Dado o postulado para a adição de ângulos, os ângulos A e B juntos formam a linha ABC. Por substituição, A e B juntos são 180°, portanto, são ângulos suplementares. Q.E.d. 

Por exemplo: Prove que dois ângulos formando um par linear (ângulo A e ângulo B) são suplementares. Dado: ângulo A e ângulo B formam um par linear Demonstração: o ângulo A é suplementar ao ângulo B. 
Não use variáveis em sua prova que ainda não estão definidas. Por exemplo: Variáveis são as medidas do ângulo A e do ângulo B. 
Edite as etapas no início e no final para ver se são semelhantes. Use os dados, definições que você aprendeu e evidências semelhantes. Faça perguntas a si mesmo ao longo do caminho. `Porque isto é assim?` e `Existe alguma maneira de isso ser falso?` são boas perguntas para qualquer reclamação ou reclamação. Não se esqueça de escrever os passos na ordem correta para a prova final. Por exemplo: Se os ângulos A e B são suplementares, então eles devem ser 180° juntos. Os dois ângulos juntos formam a linha ABC. Você sabe que eles formam uma linha por causa da definição de pares lineares. Como uma linha reta mede 180°, você pode usar a substituição para provar que o ângulo A e o ângulo B somam 180°. 
Comece declarando as suposições com as quais você está trabalhando. Divida-os em etapas simples e diretas para que o leitor não precise se perguntar como uma etapa segue logicamente de outra. Não é incomum formular várias provas. Continue reorganizando até que todas as etapas estejam na ordem mais lógica. Por exemplo: comece no início. Ângulo A e ângulo B formam um par linear. O ângulo ABC é reto. Ângulo ABC é 180°. Ângulo A + ângulo B = ângulo ABC. Ângulo A + ângulo B = 180°. O ângulo A é suplementar ao ângulo B. 
As exceções ao uso de abreviaturas são: ex. (por exemplo) e d.C.z. (isto é), mas certifique-se de usá-los corretamente. 
Tentando aplicar sua evidência a um caso em que falso deveria ser, e verifique se este é realmente o caso. Se o resultado não for falso, modifique a prova para que seja. Muitas provas geométricas são escritas como uma prova de duas colunas, com a afirmação e a prova. Uma prova matemática formal destinada à publicação é escrita como gramática correta de parágrafo. 
Q.E.d. significa `quod erat demonstrandum` (latim para `o que tinha que ser provado`). Se você não tem certeza se sua prova está correta, apenas escreva em poucas frases qual é sua conclusão e por que ela é significativa.
Formulando provas matemáticas
Contente
Provas matemáticas podem ser difíceis, mas com o conhecimento básico de matemática e da estrutura de uma prova, você certamente pode formulá-las com sucesso. Infelizmente, não há uma maneira rápida e fácil de aprender a construir provas. Você precisa de uma base sólida em seu conhecimento do assunto para criar os teoremas e definições corretos para desenvolver sua prova logicamente. Ao ler exemplos e praticar você mesmo, você será capaz de dominar a habilidade de provas matemáticas.
Degraus
Método 1 de 3: Entendendo o problema

1. Entenda a pergunta. Você deve primeiro determinar exatamente o que está tentando provar. Esta questão também servirá como o teorema final da prova. Nesta etapa, você também definirá as premissas com as quais trabalhará. Identificar a pergunta e fazer as suposições necessárias fornece um ponto de partida para entender o problema e elaborar as evidências.

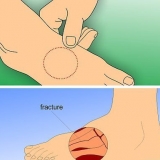
2. Desenhar diagramas. Ao tentar entender o funcionamento interno de um problema de matemática, às vezes é mais fácil desenhar um diagrama do que está acontecendo. Os diagramas são particularmente importantes em provas geométricas porque permitem visualizar o que você realmente quer provar.

3. Estudo de provas de teoremas relacionados. Provas são difíceis de aprender a compor, mas uma excelente maneira de aprender isso é estudar teoremas relacionados e como eles foram provados.

4. Pergunte. É perfeitamente normal ficar preso em evidências. Pergunte ao seu professor ou colegas se você não consegue descobrir. Este último pode ter perguntas semelhantes e você pode trabalhar juntos nas questões. Melhor fazer perguntas e depois entender do que percorrer cegamente as evidências.
Método 2 de 3: Estruturando uma prova

1. Defina provas matemáticas. Uma prova matemática é uma série de afirmações lógicas apoiadas por teoremas e definições, que provam a exatidão de outra afirmação matemática. As provas são a única maneira de saber se uma afirmação é matematicamente válida.
- Ser capaz de formular uma prova matemática indica uma compreensão fundamental do problema em si e de todos os conceitos envolvidos no problema.
- A evidência também força você a olhar para a matemática de uma maneira nova e empolgante. Apenas tentando provar algo, você ganha mais conhecimento e compreensão sobre isso, mesmo que sua evidência, em última análise, não pareça correta.

2. Conheça seu público. Antes de escrever uma prova, você precisa pensar no público para o qual está escrevendo e no que eles já sabem. Se você escrever uma prova para uma publicação, você o fará de maneira diferente de uma turma do ensino médio.

3. Entenda o tipo de evidência que você está formulando. Existem alguns tipos diferentes de provas, e a que você escolher dependerá do seu público-alvo e da atribuição. Se você não tiver certeza de qual versão usar, peça conselhos ao seu professor. No ensino médio, você deve formular a prova em um formato específico, como uma prova formal de duas colunas.

4. Escreva a prova em duas colunas como uma visão geral. Estruturar uma prova em duas colunas é uma maneira fácil de organizar seus pensamentos e considerar o problema. Desenhe uma linha no centro da página e escreva todos os dados e declarações à esquerda. Escreva as definições/declarações correspondentes à direita, ao lado dos dados que eles suportam.

5. Converter a prova em duas colunas para uma prova informal. A partir da prova em duas colunas, escreva uma prova informal como um parágrafo sem muitos símbolos e abreviaturas.
Método 3 de 3: Formulando a evidência

1. Aprenda o vocabulário da prova matemática. Existem certas declarações e frases que você vê repetidamente em uma prova matemática. Estas são as frases com as quais você deve estar familiarizado e ser capaz de usar ao formular suas próprias evidências.
- `Se A, então B` significa que você tem que mostrar que se A é verdadeiro, B também deve ser verdadeiro.
- `A se e somente se B` significa que você tem que provar que A e B são verdadeiros e falsos ao mesmo tempo. Prove tanto `Se A, então B` e `Se não A, então não B`.
- `A somente se B` significa o mesmo que `Se A, então B`, por isso não é frequentemente usado. É bom estar ciente disso quando você se deparar com isso.
- Ao preparar as provas, evite usar "eu" em favor de "nós".

2. Registre todos os dados. Ao compilar uma prova, o primeiro passo é identificar e registrar todos os dados. Este é o melhor lugar para começar, pois ajudará você a pensar sobre o que é conhecido e quais informações você precisa para concluir a prova. Leia o problema e anote cada detalhe.

3. Definir todas as variáveis. Além de escrever os dados, é útil definir todas as variáveis. Escreva as definições no início da prova para evitar confusão para o leitor. Se as variáveis não forem definidas, um leitor pode facilmente se perder ao tentar entender sua evidência.

4. Trabalhe com as evidências de trás para frente. Muitas vezes é mais fácil pensar para trás sobre um problema. Comece com a conclusão, o que você está tentando provar e pense nas etapas que podem levá-lo de volta ao início.

5. Coloque seus passos em ordem lógica. Comece a prova no início e trabalhe até a conclusão. Embora seja útil pensar sobre as evidências, começando com a conclusão e trabalhando de trás para frente, apresentar as evidências reais colocará a conclusão no final. As afirmações nas provas devem seguir umas das outras, com fundamentação para cada afirmação, para que não haja motivos para duvidar da validade de suas provas.

6. Evitar o uso de setas e abreviaturas nas provas escritas. Ao esboçar o plano para sua prova, você pode usar taquigrafia e símbolos, mas ao escrever a prova final, símbolos, como setas, podem confundir o leitor. Use palavras como "então" ou "então" em vez disso.

7. Apoie todas as declarações com um teorema, lei ou definição. Uma prova é tão boa quanto a prova usada. Você não pode fazer uma reclamação sem fundamentar com uma definição. Consulte outras evidências semelhantes como exemplo.

8. Termine com uma conclusão ou Q.E.d. A última afirmação da prova deve ser a hipótese que você estava tentando provar. Depois de ter feito esta afirmação, feche a prova com um símbolo final, como Q.E.d. ou um quadrado fechado, para indicar que a prova está completa.
Pontas
- Seus dados devem estar todos relacionados à sua prova final. Se um dado não contribui em nada, você pode excluí-lo.
Artigos sobre o tópico "Formulando provas matemáticas"
Оцените, пожалуйста статью
Popular