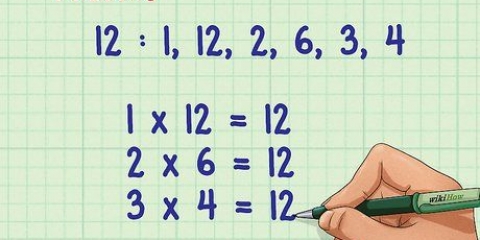Exemplo: a seguinte expressão 2x + 4(5 + 2) + 3 - (3 + 4/2). Primeiro resolva os termos entre parênteses, então 5 + 2 e 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. O termo entre o segundo par de colchetes se torna 5 porque primeiro temos que calcular 4/2 e só então calcular a adição. Se simplesmente trabalhássemos da esquerda para a direita, a soma seria 3 + 4 : 2, sendo que primeiro 3 + 4 e depois 7/2 seriam calculados, resultando na resposta errada 7/2. Nota – se vários colchetes estiverem aninhados (parênteses entre colchetes), dissolva o interno primeiro e trabalhe em direção aos colchetes externos. 
Depois de resolver os parênteses, o exemplo ficou assim. 2x + 4(7) + 3 - 5. A única potência em nosso exemplo é 3, e isso é igual a 9. A expressão agora se torna 2x + 4(7) + 9 - 5. 
Existem duas multiplicações no problema: 2x (2x é 2 × x) e 4(7). Não sabemos o valor de x, então vamos deixar como 2x. 4(7) = 4 × 7 = 28. Podemos escrever isso de forma diferente como 2x + 28 + 9 - 5. 
Como já resolvemos um problema de divisão que estava entre parênteses, não há mais problemas de divisão em nosso problema, então podemos pular esta etapa. Isso levanta um ponto importante - se uma operação não ocorrer em uma expressão, prossiga para a próxima operação conforme indicado nas regras de regras matemáticas. 
Nossa expressão é agora parcialmente simplificada para "2x + 28 + 9 - 5". Agora somamos o máximo possível – da esquerda para a direita. Não podemos adicionar 2x aos outros números, porque não sabemos o valor de x, então pulamos este. 28 + 9 = 37, podemos reescrever a expressão como "2x + 37 - 5". 
Em nossa expressão, "2x + 37 - 5", há apenas uma subtração,37 - 5 = 32 
Nossa resposta final é "2x + 32". Não podemos resolver a adição sem saber o valor de x, mas quando o fazemos, é muito mais fácil resolver do que a expressão original. 

Por exemplo, suponha que temos que resolver a fração 36/60. Se tivermos uma calculadora em mãos, a resposta (6) é calculada assim. Se não tivermos isso, podemos percorrer um longo caminho eliminando fatores semelhantes. Outra maneira de pensar em 36/60 é como (6 × 6)/(6 × 10). Isso pode ser reescrito novamente como 6/6 × 6/10. 6/6 = 1, então nossa expressão se torna 1 × 6/10 = 6/10. Mas ainda não chegamos lá - tanto 6 quanto 10 têm o mesmo fator de 2. Repetindo o procedimento acima, mantemos3/5 cerca de. 
Suponha que temos a expressão (3x + 3x)/(-3x + 15x).Esta fração pode ser reescrita como (x + 1)(3x)/(3x)(5 - x), 3x ocorre tanto no numerador quanto no denominador. Removendo esses fatores da equação dá (x + 1)/(5 - x). Da mesma forma, este é o caso da equação (2x + 4x + 6)/2. Como todo termo é divisível por 2, podemos reescrevê-lo como (2(x + 2x + 3))/2 e assim simplificar para x + 2 x + 3. Lembre-se, você não pode eliminar todos os termos - apenas os fatores que estão no numerador e no denominador. Por exemplo, a expressão (x(x + 2))/x, onde o "X" pode ser removido da fração, deixando (x + 2)/1 = (x + 2). Mas (x + 2)/x não é para simplificar para 2/1 = 2. 
Por exemplo, a expressão 3(x + 8 pode ser simplificada para3x + 24, enquanto 3x(x + 8) pode ser simplificado para 3x + 24x. Observe que em alguns casos, como com frações variáveis, a constante fora dos parênteses pode ser usada na simplificação e, portanto, não deve ser multiplicada. Por exemplo, na fração (3(x + 8))/3x, o fator 3 ocorre tanto no numerador quanto no denominador, então podemos cancelá-lo e simplificar a expressão para (x + 8)/x. Isso é mais simples e fácil de trabalhar do que com (3x + 24x)/3x, que teria sido a resposta se tivéssemos multiplicado. 
Dê outra olhada na expressão x - 5x + 6. Isso pode ser resolvido em (x - 3)(x - 2). Então, se x - 5x + 6 é o numerador de uma equação com um desses fatores no denominador (como em (x - 5x + 6)/(2(x - 2))), então podemos fatorá-lo em fatores como que podemos nos livrar do denominador. Em outras palavras, em (x - 3)(x - 2)/(2(x - 2)), (x - 2) desaparece, deixando-nos(x - 3)/2 restou. Como indicado acima, você também pode resolver uma equação com fatoração, especialmente se for igual a zero. Por exemplo: pegue a equação x - 5x + 6 = 0. A fatoração nos dá (x - 3)(x - 2) = 0. Como um número vezes zero é igual a zero, podemos definir ambos os termos iguais a zero, para encontrar a resposta para este problema. Então a resposta da equação é x =3 e x= 2.
Simplificando expressões matemáticas
Contente
Problemas de matemática geralmente pedem uma resposta "o mais simples possível" escrever – em outras palavras, dar uma resposta da forma mais elegante possível. Embora uma expressão longa e desajeitada e uma versão mais curta e elegante tecnicamente signifiquem a mesma coisa, uma resposta geralmente não é aceita até que seja simplificada o máximo possível.Além disso, as respostas simplificadas também são mais fáceis de trabalhar. `É por isso que aprender a simplificar é uma habilidade essencial para futuros matemáticos.
Degraus
Método 1 de 2: A ordem das operações matemáticas

1. A ordem das operações. Ao simplificar expressões matemáticas, você não pode simplesmente avaliar da esquerda para a direita. Certas operações têm precedência sobre outras e, portanto, devem ser feitas primeiro. Se você não fizer isso, você pode obter a resposta errada. A ordem das operações em matemática é a seguinte: parênteses, exponenciação e enraizamento, multiplicação e divisão, adição e subtração. Um mnemônico para lembrar essa sequência é "Como devemos nos livrar do inadequado " ou "HMWVDOA".
- Observe que, embora um conhecimento básico das operações seja suficiente para resolver a maioria das expressões padrão, são necessárias técnicas especiais para resolver expressões contendo variáveis, incluindo a maioria dos polinômios. Veja o Método Dois para obter mais informações.

2. Comece resolvendo todos os termos entre parênteses. Em matemática, parênteses significam que todos os termos que eles encerram devem ser resolvidos separadamente da expressão circundante. Independentemente das operações, certifique-se de resolver primeiro todos os termos entre parênteses se quiser simplificar uma expressão. Tenha em mente que as regras de cálculo para a ordem das operações também se aplicam entre parênteses. Então aqui também primeiro parênteses, depois exponenciação, etx.

3. Agora dissolva os poderes. Depois de resolver os parênteses, agora você pode passar para a exponenciação. Resolva-os um por um.

4. Agora resolva as somas da multiplicação. Lembre-se que uma multiplicação pode ser escrita de várias maneiras. Com um ponto, sem um ponto ou com um símbolo ×. Mas também algo como 4(x)) indica uma multiplicação.

5. Continuar com problemas de divisão. Se você estiver procurando por problemas de divisão, lembre-se de que eles também podem ser escritos de maneiras diferentes. O símbolo ÷ simples, com dois pontos ou uma barra (como 3/4) todos indicam uma divisão.

6. Adicionar. Agora some os diferentes termos. Trabalhe isso da esquerda para a direita, como está na expressão e o que for mais conveniente. Por exemplo, na soma 49 + 29 + 51 +71, é mais fácil dividir o problema nos seguintes blocos: 49 + 51 = 100, 29 + 71 = 100 e 100 + 100 = 200. Isso é mais fácil do que 49 + 29 = 78, 78 + 51 = 129 e 129 + 71 = 200.

7. subtrair. O último passo das operações é subtrair os termos restantes. Trabalhe o resto da sua expressão, da esquerda para a direita. Você pode fazer a adição de números negativos nesta ou na etapa anterior - não importa para sua resposta.

8. Veja sua expressão. Depois de trabalhar com a sequência de operações, você fica com vários termos na forma mais simplificada. Se houver uma ou mais variáveis na expressão, elas permanecerão praticamente inalteradas. Simplificar expressões com variáveis requer que resolvamos essas equações ainda mais para as incógnitas ou usando métodos especiais (veja o próximo passo).
Método 2 de 2: simplificando expressões complexas

1. Adicione potências variáveis iguais. Ao lidar com expressões que contêm variáveis, é importante lembrar que termos com a mesma variável e o mesmo expoente (ou "termos iguais") podem ser somados (ou subtraídos) como números regulares. Os termos devo não só têm a mesma variável, mas também o mesmo expoente. Por exemplo, 7x e 5x podem ser somados, mas 7x e 5x não podem.
- Esta regra também pode ser estendida para termos multivariados. Por exemplo, 2xy pode ser adicionado a -3xy, mas não -3xy ou -3y.
- Tome as seguintes expressões: x + 3x + 6 - 8x. Nesta expressão, podemos somar os termos 3x e -8x porque eles são iguais entre si. Nossa expressão fica então simplificada: x - 5x + 6.

2. Simplifique frações eliminando ou dividindo fatores. Frações que consistem apenas em números (e sem variáveis) podem ser simplificadas de várias maneiras. Uma fração é apenas uma soma de divisão e deve ser tratada como tal. Além disso, se ocorrer a mesma multiplicação no numerador ou denominador, ela pode ser eliminada, pois já dão a resposta 1 quando compartilhadas. Em outras palavras, se o numerador e o denominador tiverem o mesmo fator, então ele pode ser removido da fração, simplificando o resultado.

3. Se você está lidando com frações que contêm variáveis, tente eliminar as variáveis. Essas expressões oferecem possibilidades únicas para simplificar. Assim como as frações regulares, as frações variáveis permitem remover fatores que estão tanto no numerador quanto no denominador. Mas, no último caso, esses fatores podem ser tanto números quanto variáveis.

4. Multiplique os termos entre parênteses por suas constantes. Ao lidar com termos variáveis entre parênteses mais uma constante, multiplicar qualquer termo dentro dos parênteses pela constante fora dos parênteses pode resultar em uma expressão mais simples.Isso se aplica a constantes numéricas e constantes com variáveis.

5. Simplifique por fatoração. Esta é uma técnica que pode simplificar algumas equações. Ao fatorar, pense em algo que seja o oposto de "multiplicando parênteses" – às vezes uma equação pode ser representada mais simplesmente como dois termos multiplicados juntos do que como uma equação. Isso é especialmente verdadeiro se você puder eliminar parte da equação com ele. Em certos casos (como nas equações do segundo grau), você também pode resolver a própria equação com fatoração.
Artigos sobre o tópico "Simplificando expressões matemáticas"
Оцените, пожалуйста статью
Popular