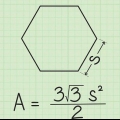
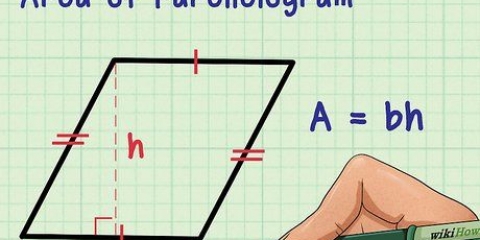A fórmula para calcular o comprimento do apótema é a seguinte: o comprimento do lado (s) dividido por 2 vezes a tangente (tan) de 180 graus, dividido pelo número de lados (n). 

O perímetro é 6 x 10 (n X s) é igual a 60 (então p = 60). O apótema é calculado ligando 6 e 10 para o n e s da fórmula. O resultado de 2tan(180/6) é 1,1547, e então dividimos 10 por 1,1547 - o que equivale a 8,66. A área do polígono é uma = uma X p / 2 ou 8,66 multiplicado por 60 dividido por 2. A solução é uma área de 259,8. Observe que não há parênteses no "superfície"-equação, então 8,66 dividido por 2 multiplicado por 60 dá o mesmo resultado, assim como 60 dividido por 2 multiplicado por 8,66. 


Encontrando a área de polígonos regulares
Contente
Um polígono regular é uma figura convexa bidimensional com lados congruentes e ângulos iguais. Para muitos polígonos, como quadriláteros ou triângulos Existem fórmulas simples para encontrar sua área, mas se você estiver lidando com um polígono, provavelmente é melhor escolher uma fórmula que use o apótema e o perímetro da forma. Com um pouco de esforço você pode encontrar a área de polígonos regulares em apenas alguns minutos.
Degraus
Parte 1 de 2: Calculando o perímetro

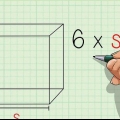
1. Calcule a circunferência. O perímetro é o comprimento combinado do perímetro de uma figura bidimensional. Para um polígono regular, isso pode ser calculado multiplicando o comprimento de um lado pelo número de lados (n) da figura.

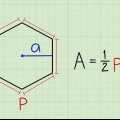
2. Determine o apótema. O apótema de um polígono regular é a distância mais curta de seu centro para ambos os lados, criando um ângulo reto. Isso é um pouco mais difícil de determinar do que a circunferência.

3. Conheça a fórmula certa. A área de um polígono regular é dada pela fórmula:Área = (uma X p)/2,através do qual uma é o comprimento do apótema, e p o perímetro do polígono.

4. Insira os valores deuma e p na fórmula para calcular o perímetro. Como exemplo, vamos pegar um hexágono (6 lados) com comprimento 10 para cada lado (s).
Parte 2 de 2: Entendendo os conceitos de uma maneira diferente

1. Um polígono regular pode ser considerado como uma coleção de triângulos. Cada lado representa a base de um triângulo, e há tantos triângulos no polígono quanto os lados. Cada um dos triângulos são iguais em base, altura e área.

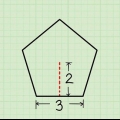
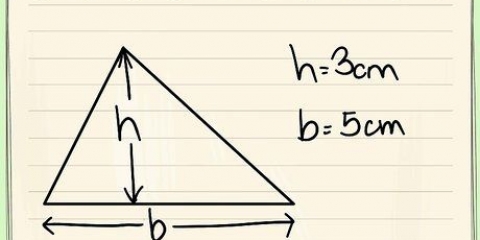
2. Use a fórmula da área de um triângulo. A área de um triângulo é 1/2 do comprimento de sua base (que é igual a um lado de um polígono), multiplicado por sua altura (que é igual ao apótema de um polígono regular).

3. Observe as semelhanças. Novamente, a fórmula para um polígono regular é 1/2 vezes o apótema multiplicado pelo perímetro. O perímetro é o comprimento de um lado multiplicado pelo número de lados (n); em um polígono regular representa n também o número de triângulos que compõem a figura. Então a fórmula nada mais é do que a área de um triângulo multiplicada pelo número de triângulos no polígono.
Pontas
- Veja o wikiHow para mais informações sobre como trabalhar com raízes quadradas e raízes cúbicas.
- Se o desenho do seu octógono (ou qualquer outra forma) for dividido em triângulos e a área de um triângulo for rotulada, você não precisará mais do apótema. Basta pegar a área desse triângulo e multiplicá-lo pelo número de lados no polígono original.
Artigos sobre o tópico "Encontrando a área de polígonos regulares"
Оцените, пожалуйста статью
Popular