Instruções gratuitas passo a passo 
Este valor é o valor x em sua equação de inclinação, onde inclinação = y/x. Então, se você mediu 7, sua equação será "inclinação = y/7". 
Este montante é o oposto ou valor y na sua equação de inclinação. Então, se você mediu 5, a equação se torna "inclinação = 5/7". 
Então, para continuar o exemplo, a equação se torna `inclinação = 5/7` e isso é 0,71428571. 
Para continuar com o exemplo, uma inclinação de 0,71428571 dá um ângulo de 35,5 graus. 
Efetivamente, você criou um pequeno ângulo reto no ângulo obtuso que deseja medir, tornando o raio superior do ângulo obtuso a hipotenusa do seu ângulo reto. 
Você determina a inclinação do ângulo do triângulo agudo, com o qual você pode calcular os graus no ângulo agudo. A linha de fundo é o adjacente valor na equação `inclinação = oposto/adjacente`. 
O comprimento de sua linha vertical é o oposto valor na equação `inclinação = oposto/adjacente`. Se você conhece os valores tanto do lado oposto quanto do adjacente, pode calcular a inclinação do ângulo agudo. 
Por exemplo, a equação `inclinação = 2/4` produzirá uma inclinação de 0,5. 
Para continuar com o exemplo, se sua inclinação for 0,5, o ângulo agudo será um ângulo de 26,565 graus. 
Para continuar com o exemplo, se você tem um ângulo agudo de 26,565 graus, você tem um ângulo obtuso de 153,435 graus (180 – 26,565 = 153,435). 
A linha horizontal será o lado adjacente do seu triângulo e a linha vertical será o lado oposto do ângulo agudo que você deseja medir. 
Meça a linha horizontal do vértice até o ponto onde ela intercepta a linha vertical. Meça a linha vertical do ponto onde ela intercepta a linha horizontal até o ponto onde ela intercepta a linha diagonal. 
Por exemplo, se sua linha horizontal for 8 e a linha vertical for 4, sua equação se tornará "inclinação = 4/8". A inclinação do seu ângulo é então 0,5. 
Para continuar com o exemplo, se sua inclinação for 0,5, o ângulo agudo será 26,565 graus. 
Para continuar com o exemplo, se o ângulo agudo menor for 26,565 graus, então o ângulo reflexo será 333,435 graus.
Medindo um ângulo sem um transferidor
Contente
A maneira mais fácil de medir um ângulo é com um transferidor. No entanto, se você não tiver um transferidor à mão, poderá determinar o tamanho de um ângulo usando os princípios geométricos básicos dos triângulos. Você precisa de uma calculadora científica para resolver as equações. A maioria dos smartphones está equipada com ele, mas você também pode baixar aplicativos gratuitos ou usar uma calculadora gratuita online. Os cálculos que você precisa fazer dependem se você está lidando com um ângulo agudo (menos de 90 graus), ângulo obtuso (mais de 90 graus, mas menos de 180) ou um `ângulo reflexo` (mais de 180 graus, mas menos) . do que 360).
Degraus
Método 1 de 3: canto agudo
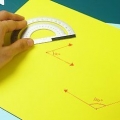
1. Desenhe uma linha vertical conectando os dois raios do ângulo. Para encontrar o número de graus em um ângulo agudo, conecte os dois raios para formar um triângulo. Alinhe a extremidade curta da régua com o raio inferior e desenhe uma linha vertical cruzando o outro raio usando o lado longo da régua.
- A linha vertical cria um triângulo retângulo. O ângulo formado pelo lado adjacente (o raio inferior do ângulo) do triângulo e o lado oposto (a linha vertical) é de 90 graus.
2. Meça o comprimento do lado adjacente em torno do lado adjacente ou valor x achar. Coloque a extremidade de sua régua no vértice. Meça o comprimento do lado adjacente do vértice ao ponto onde ele intercepta o lado oposto.
3. Medimos o comprimento do outro lado para encontrar o oposto. Alinhe a extremidade curta da régua com o lado adjacente do triângulo. Meça o comprimento da linha vertical do ponto onde ela encontra o lado adjacente até o ponto onde ela encontra o raio superior do canto (a hipotenusa do seu triângulo).
4. Divida o oposto pelo adjacente (o valor de y pelo valor de x) para encontrar a inclinação do ângulo. A inclinação é a inclinação da linha diagonal, ou hipotenusa, do seu triângulo. Depois de conhecer esse número, você pode calcular os graus do seu ângulo agudo.
Dica: Não arredonde o número antes de convertê-lo em graus - caso contrário, o resultado será menos preciso.
5. Use sua calculadora para calcular o ângulo em graus. Digite o valor da inclinação em sua calculadora científica e pressione o botão tangente inversa (tan). Isso lhe dará o ângulo em graus.
Método 2 de 3: Ângulo obtuso
1. Estender o raio inferior do canto em uma linha reta. Marque seu vértice com um ponto e, em seguida, use o lado comprido da régua para desenhar uma linha reta à esquerda do vértice. O raio inferior do canto deve ser uma única linha longa que se estende abaixo do raio superior aberto do canto.
- Certifique-se de que a linha esteja perfeitamente reta. Se a linha estiver inclinada para cima ou para baixo, isso arruinará a precisão da sua equação.
Dica: Se estiver trabalhando em papel sem pauta, você pode alinhar o lado curto da régua com o lado do papel para garantir que a extensão da linha esteja reta.
2. Desenhe uma linha vertical conectando o raio superior à linha. Alinhe o lado curto de sua régua com o raio inferior em um ponto onde o lado longo cruza o raio superior. Siga o lado longo para desenhar uma linha reta a partir da viga inferior conectando os dois.
3. Meça o comprimento da linha inferior do vértice. Coloque sua régua abaixo da linha inferior, começando na linha vertical criando o ângulo reto. Meça o comprimento dessa interseção até o vértice do ângulo original.
4. Meça o comprimento da linha vertical. Alinhe a extremidade curta de sua régua com a linha inferior do pequeno triângulo agudo. Meça com a régua até o ponto onde a linha vertical cruza o raio aberto do seu ângulo obtuso. Este é o comprimento da sua linha vertical.
5. Determine a inclinação do ângulo agudo. Compartilhe o oposto valor pelo adjacente valor para determinar a inclinação do ângulo agudo. Você usará este valor para calcular o ângulo agudo em graus.
6. Calcule os graus do ângulo agudo. Digite a inclinação em sua calculadora científica e pressione o botão `tan inverso`. O valor exibido é o número de graus do ângulo agudo.
7. Subtraia o número de graus do ângulo agudo de 180. Uma linha plana é um ângulo reto com 180 graus. Como você desenhou uma linha reta, a soma do ângulo agudo que você calculou e o ângulo obtuso será de 180 graus. Subtraindo os graus do ângulo agudo de 180 dá-lhe o número de graus do seu ângulo obtuso.
Método 3 de 3: Ângulo reflexo (ângulo obtuso > 180)
1. Determine o menor ângulo agudo associado ao ângulo obtuso que é maior que 180 graus (doravante: ângulo reflexo). Um ângulo reflexo é maior que 180 graus, mas menor que 360 graus. Isso significa que, se você olhar para o ângulo reflexo, também verá um ângulo agudo dentro dele.
- Ao determinar o número de graus do ângulo agudo, você pode calcular o número de graus do ângulo reflexo. Você pode usar a equação básica da inclinação e a função da tangente inversa em sua calculadora científica para encontrar os graus do ângulo agudo.
Dica: Se você está confuso porque o ângulo está de cabeça para baixo, vire o papel e ignore o ângulo reflexo até o último passo.
2. Desenhe uma linha vertical conectando os raios do ângulo agudo. Alinhe a extremidade curta de sua régua com o raio do canto que é horizontal em vez de diagonal. Em seguida, desenhe uma linha vertical que cruza o raio horizontal do canto.
3. Meça a linha oposta e adjacente do ângulo agudo. Na equação `inclinação = oposto/adjacente`, o oposto é o comprimento da linha vertical ou o lado oposto do seu triângulo. Adjacente é o comprimento da linha horizontal ou o lado adjacente do seu triângulo.
4. Divida o oposto pelo adjacente para calcular a inclinação do ângulo agudo. Use os valores encontrados para o comprimento das linhas verticais e horizontais em sua equação de inclinação. Quando você divide o comprimento da linha vertical pelo comprimento da linha horizontal, obtém a inclinação do ângulo.
5. Use sua calculadora para encontrar os graus do ângulo agudo. Digite o valor que você tem para a inclinação do ângulo em sua calculadora científica e pressione o botão `tangente inversa` (tan). O valor exibido é o número de graus do ângulo agudo menor.
6. Subtraia o número de graus do ângulo agudo de 360. Um círculo tem 360 graus. Como um ângulo reflexo é um ângulo maior que 180 graus, considere-o parte de um círculo. Os graus do ângulo reflexo e os graus do ângulo agudo menor somam 360.
Pontas
- Verifique se as funções trigonométricas da sua calculadora científica estão definidas em graus, não em radianos.
- A inclinação é a relação entre o movimento x e o movimento y. A unidade de medida que você usa para quantificar os comprimentos das duas linhas é irrelevante - apenas certifique-se de usar a mesma unidade para ambas as linhas. Em outras palavras, se você medir o comprimento de uma linha em centímetros, você também deve medir a outra em centímetros.
Necessidades
- Calculadora científica
- Governante
Artigos sobre o tópico "Medindo um ângulo sem um transferidor"
Оцените, пожалуйста статью
Popular
