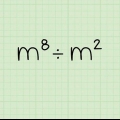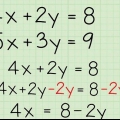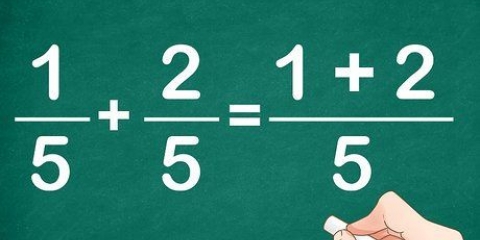Dez elevado a três











Como mostrado aqui, você pode continuar multiplicando a base pelo produto de cada um dos primeiros pares de números, até obter a resposta final. Apenas continue multiplicando os dois primeiros números, depois multiplique esta resposta pelo próximo número na sequência. Isso vale para qualquer expoente. Quando você terminar com o exemplo, você obtém  .
. 




Use um mecanismo de pesquisa como Startpage, Duckduckgo ou Google para encontrar a resposta. Você pode usar o botão `^` no seu computador, tablet ou smartphone para inserir a expressão na caixa de pesquisa, e você verá imediatamente a resposta e sugestões de expressões semelhantes para explorar (Duckduckgo até mostra uma calculadora completa). 





Como tudo é o mesmo número, mas multiplicado, podemos combiná-los: 




Como as bases são as mesmas, você pode apenas adicioná-las: 




Como você verá em breve, qualquer número que faça parte de uma fração, como  , ser reescrito como
, ser reescrito como  . Expoentes negativos formam frações.
. Expoentes negativos formam frações. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Lembre-se que um número sem uma potência tem um expoente de 1
Lembre-se que um número sem uma potência tem um expoente de 1 =
= 
 =
= 




![Resolvendo expoentes x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Resolvendo expoentes ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Resolvendo expoentes
Contente
Expoentes são usados quando um número é multiplicado por ele mesmo. Em vez de 



Degraus
Método 1 de 3: Resolvendo expoentes simples

1. Aprenda os termos e vocabulário corretos para problemas exponenciais. Você tem um expoente como  , então você trabalha com duas partes simples. O número do chassi aqui é 2, ou o base. Este número é elevado à potência de 3, também conhecido como expoente ou potência. Estamos falando sobre
, então você trabalha com duas partes simples. O número do chassi aqui é 2, ou o base. Este número é elevado à potência de 3, também conhecido como expoente ou potência. Estamos falando sobre  , então dizemos `dois à terceira`, `dois à terceira potência`, ou `dois aumentos à terceira potência`.`
, então dizemos `dois à terceira`, `dois à terceira potência`, ou `dois aumentos à terceira potência`.`
 , então você trabalha com duas partes simples. O número do chassi aqui é 2, ou o base. Este número é elevado à potência de 3, também conhecido como expoente ou potência. Estamos falando sobre
, então você trabalha com duas partes simples. O número do chassi aqui é 2, ou o base. Este número é elevado à potência de 3, também conhecido como expoente ou potência. Estamos falando sobre  , então dizemos `dois à terceira`, `dois à terceira potência`, ou `dois aumentos à terceira potência`.`
, então dizemos `dois à terceira`, `dois à terceira potência`, ou `dois aumentos à terceira potência`.` - Se um número for elevado à segunda potência, como
, então você também pode dizer que o número é ao quadrado é, como `cinco ao quadrado.`
- Se um número for elevado à terceira potência, como
, então você também pode dizer que o número a número do cubo é.
- Se um número sem expoente for mencionado, como 4, por exemplo, então, em teoria, ele está na primeira potência e pode ser reescrito como
.
- Se o expoente for igual a 0 e um `número (diferente de zero)` for elevado à `potência zero`, então o inteiro será igual a 1, como
ou mesmo algo como
Mais sobre isso na seção `Dicas`.

2. Multiplique a base o número de vezes por ela mesma conforme indicado pelo expoente. Se você tiver que resolver uma potência manualmente, comece reescrevendo-a como uma multiplicação. Você multiplica a base o número de vezes por ela mesma, conforme indicado pelo expoente. Então, você tem  então você multiplica três quatro vezes por ele mesmo
então você multiplica três quatro vezes por ele mesmo  . Mais alguns exemplos são:
. Mais alguns exemplos são:
 então você multiplica três quatro vezes por ele mesmo
então você multiplica três quatro vezes por ele mesmo  . Mais alguns exemplos são:
. Mais alguns exemplos são:



3. Resolva uma expressão: Multiplique os dois primeiros números juntos para obter o produto. Por exemplo, com  , você começa com
, você começa com  Isso parece uma tarefa tediosa, mas basta fazê-lo passo a passo. Comece a multiplicar os dois primeiros quatros. Em seguida, substitua os dois quatros pela resposta, conforme mostrado abaixo:
Isso parece uma tarefa tediosa, mas basta fazê-lo passo a passo. Comece a multiplicar os dois primeiros quatros. Em seguida, substitua os dois quatros pela resposta, conforme mostrado abaixo:
 , você começa com
, você começa com  Isso parece uma tarefa tediosa, mas basta fazê-lo passo a passo. Comece a multiplicar os dois primeiros quatros. Em seguida, substitua os dois quatros pela resposta, conforme mostrado abaixo:
Isso parece uma tarefa tediosa, mas basta fazê-lo passo a passo. Comece a multiplicar os dois primeiros quatros. Em seguida, substitua os dois quatros pela resposta, conforme mostrado abaixo:



4. Multiplique a resposta do primeiro par (16) pelo próximo número. Continue multiplicando os números para `crescer` seu expoente. Continuando com nosso exemplo, multiplicamos 16 pelos próximos 4 para que:






 .
.
5. Tente também os exemplos a seguir e verifique suas respostas com uma calculadora.




6. Use o `exp`, `X n  botão ` ou `^` da sua calculadora para os expoentes. É quase impossível encontrar expoentes maiores, como
botão ` ou `^` da sua calculadora para os expoentes. É quase impossível encontrar expoentes maiores, como  à mão, mas as calculadoras podem lidar com isso facilmente. O botão para isso geralmente é indicado com bastante clareza. A calculadora do Windows pode ser expandida para uma calculadora científica clicando na guia `Exibir` da calculadora e selecionando `Científica`. Se você quiser a calculadora padrão de volta, clique em `Visualizar` novamente e selecione `Padrão`.
à mão, mas as calculadoras podem lidar com isso facilmente. O botão para isso geralmente é indicado com bastante clareza. A calculadora do Windows pode ser expandida para uma calculadora científica clicando na guia `Exibir` da calculadora e selecionando `Científica`. Se você quiser a calculadora padrão de volta, clique em `Visualizar` novamente e selecione `Padrão`.
 botão ` ou `^` da sua calculadora para os expoentes. É quase impossível encontrar expoentes maiores, como
botão ` ou `^` da sua calculadora para os expoentes. É quase impossível encontrar expoentes maiores, como  à mão, mas as calculadoras podem lidar com isso facilmente. O botão para isso geralmente é indicado com bastante clareza. A calculadora do Windows pode ser expandida para uma calculadora científica clicando na guia `Exibir` da calculadora e selecionando `Científica`. Se você quiser a calculadora padrão de volta, clique em `Visualizar` novamente e selecione `Padrão`.
à mão, mas as calculadoras podem lidar com isso facilmente. O botão para isso geralmente é indicado com bastante clareza. A calculadora do Windows pode ser expandida para uma calculadora científica clicando na guia `Exibir` da calculadora e selecionando `Científica`. Se você quiser a calculadora padrão de volta, clique em `Visualizar` novamente e selecione `Padrão`.Método 2 de 3: somando, subtraindo e multiplicando expoentes

1. Você só pode adicionar ou subtrair números de potência um do outro se eles tiverem a mesma base e o mesmo expoente. Se você estiver lidando com bases e expoentes idênticos, como  , então você pode simplificar a adição dos termos a uma multiplicação. Não esqueça isto
, então você pode simplificar a adição dos termos a uma multiplicação. Não esqueça isto  pode ser considerado como
pode ser considerado como  , de modo a
, de modo a  adicionando, onde `1 daquele + 1 daquele = 2 daquele`, qualquer que seja `aquilo`. Basta somar o número de termos semelhantes (aqueles com base e expoente idênticos) e multiplicar a soma por essa expressão exponencial. Você pode então
adicionando, onde `1 daquele + 1 daquele = 2 daquele`, qualquer que seja `aquilo`. Basta somar o número de termos semelhantes (aqueles com base e expoente idênticos) e multiplicar a soma por essa expressão exponencial. Você pode então  resolva e multiplique essa resposta por dois. Lembre-se que isso é possível porque uma multiplicação nada mais é do que reescrever uma adição, porque
resolva e multiplique essa resposta por dois. Lembre-se que isso é possível porque uma multiplicação nada mais é do que reescrever uma adição, porque  . Aqui estão alguns exemplos:
. Aqui estão alguns exemplos:
 , então você pode simplificar a adição dos termos a uma multiplicação. Não esqueça isto
, então você pode simplificar a adição dos termos a uma multiplicação. Não esqueça isto  pode ser considerado como
pode ser considerado como  , de modo a
, de modo a  adicionando, onde `1 daquele + 1 daquele = 2 daquele`, qualquer que seja `aquilo`. Basta somar o número de termos semelhantes (aqueles com base e expoente idênticos) e multiplicar a soma por essa expressão exponencial. Você pode então
adicionando, onde `1 daquele + 1 daquele = 2 daquele`, qualquer que seja `aquilo`. Basta somar o número de termos semelhantes (aqueles com base e expoente idênticos) e multiplicar a soma por essa expressão exponencial. Você pode então  resolva e multiplique essa resposta por dois. Lembre-se que isso é possível porque uma multiplicação nada mais é do que reescrever uma adição, porque
resolva e multiplique essa resposta por dois. Lembre-se que isso é possível porque uma multiplicação nada mais é do que reescrever uma adição, porque  . Aqui estão alguns exemplos:
. Aqui estão alguns exemplos: 
2. Multiplicar números com a mesma base somando os expoentes. Se você tiver dois expoentes com a mesma base, como  , então você só precisa adicionar os dois expoentes com a mesma base. assim,
, então você só precisa adicionar os dois expoentes com a mesma base. assim, . Se você achar isso um pouco estranho, divida-o em partes menores para entender como o sistema funciona:
. Se você achar isso um pouco estranho, divida-o em partes menores para entender como o sistema funciona:
 , então você só precisa adicionar os dois expoentes com a mesma base. assim,
, então você só precisa adicionar os dois expoentes com a mesma base. assim, . Se você achar isso um pouco estranho, divida-o em partes menores para entender como o sistema funciona:
. Se você achar isso um pouco estranho, divida-o em partes menores para entender como o sistema funciona:






3. Multiplique um número exponencial elevado a outra potência, como ( X 2 ) 5  . Se você elevar um número a uma determinada potência e o todo for elevado a uma determinada potência, basta multiplicar os dois expoentes. assim,
. Se você elevar um número a uma determinada potência e o todo for elevado a uma determinada potência, basta multiplicar os dois expoentes. assim,  . Se você ficar confuso, pense novamente no que esses símbolos realmente significam.
. Se você ficar confuso, pense novamente no que esses símbolos realmente significam.  significa apenas você
significa apenas você  Multiplica 5 vezes por ele mesmo, então:
Multiplica 5 vezes por ele mesmo, então:
 . Se você elevar um número a uma determinada potência e o todo for elevado a uma determinada potência, basta multiplicar os dois expoentes. assim,
. Se você elevar um número a uma determinada potência e o todo for elevado a uma determinada potência, basta multiplicar os dois expoentes. assim,  . Se você ficar confuso, pense novamente no que esses símbolos realmente significam.
. Se você ficar confuso, pense novamente no que esses símbolos realmente significam.  significa apenas você
significa apenas você  Multiplica 5 vezes por ele mesmo, então:
Multiplica 5 vezes por ele mesmo, então:



4. Pense em expoentes negativos como frações, ou o recíproco do número. Não sei o que é recíproco, não tem problema. Se você estiver lidando com um expoente negativo, como  , então faça o expoente positivo e coloque isso como o denominador abaixo de um, resultando em
, então faça o expoente positivo e coloque isso como o denominador abaixo de um, resultando em  . Aqui estão alguns exemplos adicionais:
. Aqui estão alguns exemplos adicionais:
 , então faça o expoente positivo e coloque isso como o denominador abaixo de um, resultando em
, então faça o expoente positivo e coloque isso como o denominador abaixo de um, resultando em  . Aqui estão alguns exemplos adicionais:
. Aqui estão alguns exemplos adicionais:


5. Divida dois números com a mesma base subtraindo os expoentes. A divisão é o oposto da multiplicação e, embora não sejam resolvidos exatamente como opostos, eles estão aqui. Se você está lidando com a equação  , basta subtrair o expoente superior do inferior e deixar a base como está. assim,
, basta subtrair o expoente superior do inferior e deixar a base como está. assim,  , ou 16.
, ou 16.
 , basta subtrair o expoente superior do inferior e deixar a base como está. assim,
, basta subtrair o expoente superior do inferior e deixar a base como está. assim,  , ou 16.
, ou 16. , ser reescrito como
, ser reescrito como  . Expoentes negativos formam frações.
. Expoentes negativos formam frações.
6. Experimente alguns exercícios práticos para se acostumar a trabalhar com números de potência. Os exercícios a seguir praticam tudo o que foi abordado até agora. Para a resposta, basta selecionar a linha que contém o problema.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Lembre-se que um número sem uma potência tem um expoente de 1
Lembre-se que um número sem uma potência tem um expoente de 1 =
= 
 =
= 
Método 3 de 3: Resolvendo frações como números de potência

1. Trate frações na forma de números de potência, como X 1 2  como raiz quadrada.
como raiz quadrada.  na verdade é exatamente igual
na verdade é exatamente igual  . Isso é verdade independentemente do denominador da fração, então
. Isso é verdade independentemente do denominador da fração, então  torna-se a raiz quadrática de x, também escrita como
torna-se a raiz quadrática de x, também escrita como ![Resolvendo expoentes {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 como raiz quadrada.
como raiz quadrada.  na verdade é exatamente igual
na verdade é exatamente igual  . Isso é verdade independentemente do denominador da fração, então
. Isso é verdade independentemente do denominador da fração, então  torna-se a raiz quadrática de x, também escrita como
torna-se a raiz quadrática de x, também escrita como ![Resolvendo expoentes {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - As raízes são o inverso dos expoentes. Por exemplo, se você pegar a resposta de
à quarta potência, então você volta para
, e assim pode
também ser escrito como
. Outro exemplo é
e então
e assim
.

2. Faça do numerador um expoente normal para uma fração mista. pode parecer impossível, mas é fácil se você lembrar como os expoentes são multiplicados. Faça da base uma raiz quadrada, como uma fração normal, e eleve a coisa toda à potência no topo da fração. Se você achar difícil lembrar disso, repasse a teoria novamente. Em última análise, isso se aplica
pode parecer impossível, mas é fácil se você lembrar como os expoentes são multiplicados. Faça da base uma raiz quadrada, como uma fração normal, e eleve a coisa toda à potência no topo da fração. Se você achar difícil lembrar disso, repasse a teoria novamente. Em última análise, isso se aplica  apenas igual
apenas igual  Por exemplo:
Por exemplo:
 pode parecer impossível, mas é fácil se você lembrar como os expoentes são multiplicados. Faça da base uma raiz quadrada, como uma fração normal, e eleve a coisa toda à potência no topo da fração. Se você achar difícil lembrar disso, repasse a teoria novamente. Em última análise, isso se aplica
pode parecer impossível, mas é fácil se você lembrar como os expoentes são multiplicados. Faça da base uma raiz quadrada, como uma fração normal, e eleve a coisa toda à potência no topo da fração. Se você achar difícil lembrar disso, repasse a teoria novamente. Em última análise, isso se aplica  apenas igual
apenas igual  Por exemplo:
Por exemplo:

![Resolvendo expoentes x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Resolvendo expoentes ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

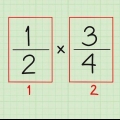
3. Você pode adicionar, subtrair e multiplicar frações na forma de números de potência – exatamente como faria normalmente. É muito mais fácil adicionar ou subtrair os expoentes antes de resolvê-los ou convertê-los em raízes quadradas. Se a base for a mesma e o expoente for o mesmo, então você pode apenas somar e subtrair. Se apenas a base for a mesma, você poderá multiplicar e dividir os expoentes como de costume, desde que leve em consideração como somar e subtrair frações. Por exemplo:


Pontas
- A maioria das calculadoras tem um botão para expoentes - pressionando após inserir a base - para resolver problemas de números de potência.Geralmente isso se parece com um ^ ou x^y.
- `Simplificar` em matemática significa faça as edições necessárias para obter a forma mais simples das expressões em questão.
- 1 é o elemento identidade dos expoentes. Isso significa que qualquer número real elevado à potência de 1 (à primeira potência) é o próprio número, por exemplo:
Além disso, 1 é o elemento de identidade da multiplicação (1 como multiplicador, como
), e da divisão (1 como dividendo, como
.
- A base zero a zero (0) é indefinida (Inglês: dne, não existe). Computadores ou calculadoras retornarão um `erro`. Lembre-se que qualquer número diferente de zero elevado à potência 0 sempre é igual a 1,
- Por exemplo, matemática superior para números imaginários é,
, através do qual
; e é uma constante irracional contínua igual a 2,71828..., e a é uma constante arbitrária. A prova pode ser encontrada na maioria dos livros de matemática superior.
Avisos
- Um aumento exponencial faz com que o produto suba cada vez mais rápido, de modo que a resposta pode parecer errada, quando estiver correta. (Verifique isso fazendo um gráfico de uma função exponencial, por exemplo.: 2, se x tiver um intervalo de valores diferentes).
Artigos sobre o tópico "Resolvendo expoentes"
Оцените, пожалуйста статью
Popular