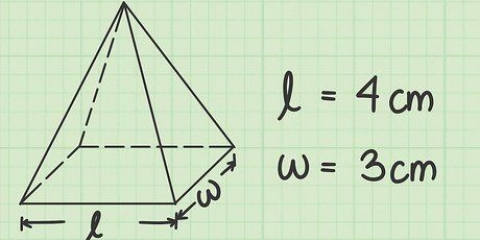Por exemplo, se o volume do prisma for 64  ), sua fórmula ficará assim:
), sua fórmula ficará assim:


Por exemplo, se a base for um retângulo de 8 metros de comprimento e 2 metros de largura, você calcularia a área da seguinte forma:



Por exemplo, se você calculou que a área da base é de 16 m, sua fórmula ficará assim:


Por exemplo, na equação  , você tem que dividir cada lado por 16 om
, você tem que dividir cada lado por 16 om  calcular. Por isso:
calcular. Por isso:


Então a altura do prisma retangular é 4 metros. 

Por exemplo, se você sabe que o volume do prisma é de 840 metros cúbicos ( ), sua fórmula ficará assim:
), sua fórmula ficará assim:


Se você conhece o comprimento dos três lados de um triângulo, pode calcular a área usando a Fórmula de Heron.ler Calcular a área de um triângulo para instruções detalhadas. Por exemplo, se a base do triângulo for 12 metros e a altura do triângulo for 7 metros, encontre a área da seguinte forma:




Por exemplo, se você sabe que a área da base é de 42 m2, sua fórmula ficará assim:


Por exemplo, na equação  , você deve dividir cada lado por 42 para determinar
, você deve dividir cada lado por 42 para determinar  . Por isso:
. Por isso:


Então, a altura do seu prisma triangular é de 20 metros. 

Por exemplo, se a área for 1460 cm, sua fórmula ficaria assim:


Por exemplo, se a base for um retângulo com 8 cm de comprimento e 2 cm de largura, encontre a área da seguinte forma:



Por exemplo, se a área da base for 16, sua fórmula ficaria assim:



Lembre-se que os lados opostos de um retângulo têm o mesmo comprimento. Por exemplo, se a base for um retângulo com 8 cm de comprimento e 2 cm de largura, encontre o perímetro da seguinte forma:



Por exemplo, se o perímetro da base for 20, sua fórmula ficaria assim:


Por exemplo, na equação  primeiro subtraia 32 de cada lado, depois divida cada lado por 20. Por isso:
primeiro subtraia 32 de cada lado, depois divida cada lado por 20. Por isso:




Então a altura do seu prisma é 71,4 cm. 

Por exemplo, se a área for 1460 cm, sua fórmula ficaria assim:


Se você conhece o comprimento dos três lados de um triângulo, pode determinar a área usando a fórmula de Heron.ler Calcular a área de um triângulo para instruções completas. Por exemplo, se a base do triângulo for 8 cm e a altura do triângulo for 4 cm, você calcularia a área da seguinte forma:




Por exemplo, se a área da base for 16, sua fórmula ficaria assim:



Por exemplo, se a base for um triângulo com comprimentos 8, 4 e 9 cm, você calcula o perímetro da seguinte forma:



Por exemplo, suponha que o perímetro da base seja 21, sua fórmula ficará assim:


Por exemplo, na equação  , você deve primeiro subtrair 32 de cada lado, depois dividir cada lado por 21. Por isso:
, você deve primeiro subtrair 32 de cada lado, depois dividir cada lado por 21. Por isso:




Então, a altura do seu prisma é 68 cm.
Calculando a altura de um prisma
Contente
- Degraus
- Método 1 de 4: Encontrando a altura de um prisma retangular de volume conhecido
- Método 2 de 4: Determinando a altura de um prisma triangular de volume conhecido
- Método 3 de 4: Encontrando a altura de um prisma retangular usando sua área
- Método 4 de 4: Determine a altura de um prisma triangular usando sua área
- Necessidades
Um prisma é uma figura tridimensional com duas bases paralelas, que são congruentes.A forma da base determina que tipo de prisma é, como um prisma retangular ou triangular. Por se tratar de uma forma 3D, não é incomum querer calcular o volume de um prisma; no entanto, você precisa da altura do prisma para isso. Encontrar a altura é possível quando você recebeu informações suficientes: o volume, a área e o perímetro da base. As fórmulas descritas nos métodos abaixo são adequadas para prismas com bases de qualquer forma, desde que você conheça a fórmula para encontrar a área dessa forma.
Degraus
Método 1 de 4: Encontrando a altura de um prisma retangular de volume conhecido

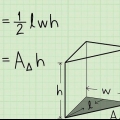
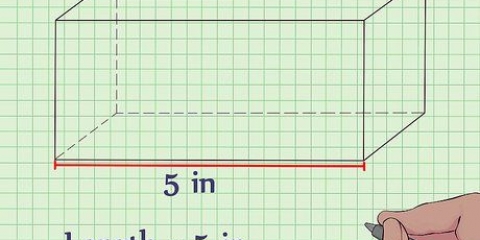
1. Use a fórmula para o volume de um prisma. O volume de um prisma pode ser encontrado pela fórmula  , através do qual
, através do qual  é igual ao volume do prisma,
é igual ao volume do prisma,  é igual à área de uma base, e
é igual à área de uma base, e  é igual à altura do prisma.
é igual à altura do prisma.
 , através do qual
, através do qual  é igual ao volume do prisma,
é igual ao volume do prisma,  é igual à área de uma base, e
é igual à área de uma base, e  é igual à altura do prisma.
é igual à altura do prisma. - A base de um prisma é um de seus lados congruentes. Como todos os lados opostos de um prisma retangular são congruentes, qualquer lado pode ser usado como plano de terra, desde que você seja consistente com seus cálculos.

2. Aplique o volume à fórmula. Se você não souber o volume, não poderá usar este método.
 ), sua fórmula ficará assim:
), sua fórmula ficará assim:

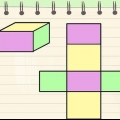
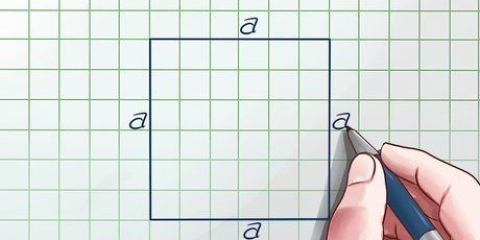
3. Encontre a área da base. Para encontrar a área, você precisa saber o comprimento e a largura da base (ou de um lado, se a base for um quadrado). Use a fórmula  determinar a área de um retângulo.
determinar a área de um retângulo.
 determinar a área de um retângulo.
determinar a área de um retângulo.


4. Substituir a área da base no volume da fórmula do prisma. Certifique-se de substituir a variável  .
.
 .
.

5. Resolva a equação para h  . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma.
 . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma. , você tem que dividir cada lado por 16 om
, você tem que dividir cada lado por 16 om  calcular. Por isso:
calcular. Por isso:

Então a altura do prisma retangular é 4 metros.
Método 2 de 4: Determinando a altura de um prisma triangular de volume conhecido

1. Escreva a fórmula para o volume de um prisma. O volume de qualquer prisma pode ser encontrado usando a fórmula  ,através do qual
,através do qual  é igual ao volume do prisma,
é igual ao volume do prisma,  é igual à área de uma base, e
é igual à área de uma base, e  é igual à altura do prisma.
é igual à altura do prisma.
 ,através do qual
,através do qual  é igual ao volume do prisma,
é igual ao volume do prisma,  é igual à área de uma base, e
é igual à área de uma base, e  é igual à altura do prisma.
é igual à altura do prisma. - A base de um prisma é um de seus lados congruentes. A base de um prisma triangular é um triângulo. Os lados são retângulos.

2. Aplique o volume à fórmula. Se você não souber o volume, não poderá usar este método.
 ), sua fórmula ficará assim:
), sua fórmula ficará assim:

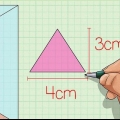
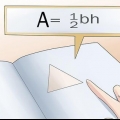
3. Encontre a área da base. Para encontrar a área, você precisa saber o comprimento da base do triângulo e a altura do triângulo. Use a fórmula  para determinar a área de um triângulo.
para determinar a área de um triângulo.
 para determinar a área de um triângulo.
para determinar a área de um triângulo.



4. Substituir a área da base no volume da fórmula do prisma. Certifique-se de substituir a variável  .
.
 .
.

5. Resolva a equação para h  . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma.
 . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma. , você deve dividir cada lado por 42 para determinar
, você deve dividir cada lado por 42 para determinar  . Por isso:
. Por isso:

Método 3 de 4: Encontrando a altura de um prisma retangular usando sua área

1. Escreva a fórmula da área de um prisma. A fórmula da área de um prisma é  , através do qual
, através do qual  é igual à superfície,
é igual à superfície,  é igual a área da base,
é igual a área da base,  é igual ao perímetro da base e
é igual ao perímetro da base e  é igual à altura do prisma.
é igual à altura do prisma.
 , através do qual
, através do qual  é igual à superfície,
é igual à superfície,  é igual a área da base,
é igual a área da base,  é igual ao perímetro da base e
é igual ao perímetro da base e  é igual à altura do prisma.
é igual à altura do prisma. - Para que esse método funcione, você precisa conhecer a área do prisma, bem como o comprimento e a largura da base.

2. Substitua a área do prisma na fórmula. Se a superfície for desconhecida, este método não funcionará.


3. Encontre a área da base. Para encontrar a área, você precisa saber o comprimento e a largura da base (ou um lado, se a base for um quadrado). Use a fórmula  determinar a área de um retângulo.
determinar a área de um retângulo.
 determinar a área de um retângulo.
determinar a área de um retângulo.


4. Substitua a área da base na fórmula da área de um prisma e simplifique. Certifique-se de preencher a carta  .
.
 .
.


5. Determine o perímetro da base. Para encontrar o perímetro de um retângulo, some os comprimentos de todos os quatro lados ou multiplique o comprimento de um lado por 4 se for um quadrado.



6. Substitua o perímetro da base na fórmula da área de um prisma. Certifique-se de substituir a letra  .
.
 .
.

7. Resolva a equação para h  . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma.
 . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma. primeiro subtraia 32 de cada lado, depois divida cada lado por 20. Por isso:
primeiro subtraia 32 de cada lado, depois divida cada lado por 20. Por isso:



Método 4 de 4: Determine a altura de um prisma triangular usando sua área

1. Escreva a fórmula da área de um prisma. A fórmula da área de um prisma é  , através do qual
, através do qual  é igual à superfície,
é igual à superfície,  é igual a área da base,
é igual a área da base,  é igual ao perímetro da base e
é igual ao perímetro da base e  é igual à altura do prisma.
é igual à altura do prisma.
 , através do qual
, através do qual  é igual à superfície,
é igual à superfície,  é igual a área da base,
é igual a área da base,  é igual ao perímetro da base e
é igual ao perímetro da base e  é igual à altura do prisma.
é igual à altura do prisma. - Para que esse método funcione, a área do prisma deve ser conhecida, assim como a área da base triangular e o comprimento dos três lados da base.

2. Substitua a área do prisma na fórmula. Se a superfície não for conhecida, este método não funcionará.


3. Encontre a área da base. Para encontrar a área, você precisa saber o comprimento da base do triângulo e a altura do triângulo. Use a fórmula  para determinar a área de um triângulo.
para determinar a área de um triângulo.
 para determinar a área de um triângulo.
para determinar a área de um triângulo.



4. Substitua a área da base na fórmula pela área de um prisma e simplifique. Substituto para  .
.
 .
.


5. Determine o perímetro da base. Para encontrar o perímetro de um triângulo, some os comprimentos dos três lados.



6. Substitua o perímetro da base na fórmula da área de um prisma. Certifique-se de substituir por  .
.
 .
.

7. Resolva a equação para h  . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma.
 . Agora você sabe a altura do seu prisma.
. Agora você sabe a altura do seu prisma. , você deve primeiro subtrair 32 de cada lado, depois dividir cada lado por 21. Por isso:
, você deve primeiro subtrair 32 de cada lado, depois dividir cada lado por 21. Por isso:



Necessidades
- Caneta/lápis e papel ou calculadora (opcional)
Artigos sobre o tópico "Calculando a altura de um prisma"
Оцените, пожалуйста статью
Similar
Popular