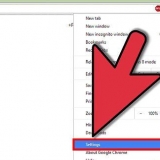
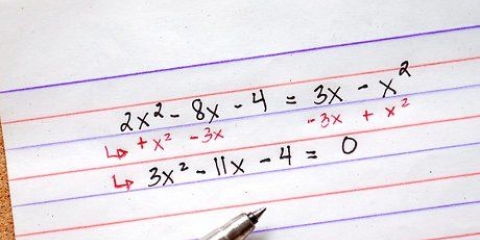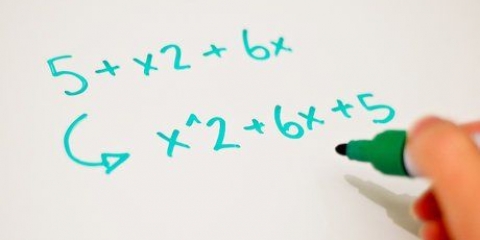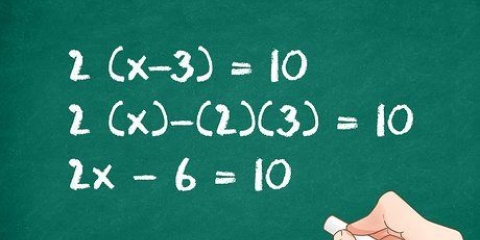3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Quadrado dividido
Contente
A quadratura é uma técnica útil para reescrever uma equação quadrática, tornando-a mais fácil de supervisionar e resolver. Você pode reescrever um quadrado reorganizando-o em partes mais gerenciáveis.
Degraus
Método 1 de 2: Parte Um: Reescrevendo uma Equação Padrão

1. Escreva a equação. Vamos supor que você queira resolver a seguinte equação: 3x - 4x + 5.

2. Remova o coeficiente da equação. Coloque os 3 colchetes externos e divida cada termo, exceto a constante, por 3. 3x dividido por 3 é x e 4x dividido por 3 é 4/3x. Então a nova equação fica assim: 3(x - 4/3x) + 5. O 5 está fora dos colchetes porque você não dividiu por 3.

3. Divida o segundo termo por 2 e quadrado. O segundo termo, também chamado de b-termo na equação, é 4/3. Reduzir pela metade o segundo termo. 4/3 ÷ 2, ou 4/3 x 1/2, é igual a 2/3. Eleve ao quadrado este termo multiplicando o numerador e o denominador por eles mesmos. (2/3) = 4/9. Escreva este termo.

4. Adição e subtração. você tem isso"adicional" termo necessário para converter os três primeiros termos da equação em um quadrado. Mas lembre-se que você adicionou este termo subtraindo-o da equação também. Claro que faz pouca diferença simplesmente combinar os termos novamente - então você estará de volta ao ponto de partida. A nova equação deve ficar assim: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Obtenha o termo que você subtraiu fora dos parênteses. Como você já está trabalhando com o 3 fora dos parênteses, não é possível colocar apenas -4/9 fora dos parênteses. Primeiro você tem que multiplicar por 3. -4/9 x 3 = -12/9, ou -4/3. Se você está lidando com uma equação que contém apenas um coeficiente 1 de x, você pode pular esta etapa.

6. Converta os termos entre parênteses em um quadrado. Sua equação agora fica assim: 3(x -4/3x +4/9). Você trabalhou de frente para trás para obter 4/9, que na verdade é outra maneira de encontrar o fator que completa o quadrado. Então você pode reescrever esses termos como: 3(x - 2/3). Você pode verificar isso multiplicando onde você verá que você obtém a mesma equação original como a resposta novamente.


7. Mesclar as constantes. Agora você tem duas constantes, 3(x - 2/3) - 4/3 + 5. Tudo o que você precisa fazer agora é adicionar -4/3 a 5 e isso dá 11/3 como resposta. Você faz isso dando a eles o mesmo denominador: -4/3 e 15/3, então somando os dois numeradores para obter 11, mantendo o denominador igual a 3.


8. Escreva a equação de outra forma. Agora você terminou. A equação final é 3(x - 2/3) + 11/3. Você pode eliminar o 3 dividindo a equação por 3, ficando com a seguinte equação:(x - 2/3) + 11/9.Agora você escreveu com sucesso a equação em outra forma: a(x - h) + k, através do qual k a constante é.
Método 2 de 2: Parte Dois: Resolvendo uma equação quadrática

1. Observe a tarefa. Vamos supor que você queira resolver a seguinte equação: 3x + 4x + 5 = 6

2. Some as constantes e coloque-as à esquerda do sinal de igual. Termos constantes são aqueles termos sem uma variável. Neste caso, você tem 5 à esquerda e 6 à direita. Você quer mover 6 para a esquerda, então subtraia 6 de ambos os lados da equação. Isso deixa 0 à direita (6-6) e -1 à esquerda (5-6). A equação agora fica assim: 3x + 4x - 1 = 0.

3. Pegue o coeficiente do quadrado fora dos colchetes. Neste caso, 3 é o coeficiente de x. Para excluir 3 dos parênteses, remova o 3, coloque o termo restante entre parênteses e divida cada termo por 3. Então, 3x ÷ 3 = x, 4x ÷ 3 = 4/3x e 1 ÷ 3 = 1/3. A equação agora fica assim: 3(x + 4/3x - 1/3) = 0.

4. Divida pela constante que você acabou de colocar entre colchetes. Com isso você finalmente se livra daqueles 3 irritantes fora dos colchetes. Ao dividir cada termo por 3, ele pode ser eliminado sem alterar a equação. Agora você tem: x + 4/3x - 1/3 = 0

5. Divida o segundo termo por 2 e quadrado. Agora pegue o segundo termo, 4/3, de b termo e dividir por 2. 4/3 2 ou 4/3 x 1/2, é 4/6 ou 2/3. E 2/3 ao quadrado é 4/9. Quando você terminar com isso, você deve escrevê-lo à esquerda e à direita da equação porque basicamente você acabou de adicionar um novo termo. Você tem que fazer isso em ambos os lados da equação. A equação agora fica assim: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Mova a constante original para o lado direito da equação e adicione-a ao termo já existente. Mova a constante, -1/3, para a direita para torná-la 1/3. Adicione isso ao outro termo, 4/9 ou 2/3. Encontre o mínimo múltiplo comum para que 1/3 e 4/9 possam ser somados. Fica assim: 1/3 x 3/3 = 3/9. Agora adicione 3/9 a 4/9 para que você tenha 7/9 no lado direito da equação. Isso dá: x + 4/3 x + 2/3 = 4/9 + 1/3 e então x + 4/3 x + 2/3 = 7/9.

7. Escreva o lado esquerdo da equação como um quadrado. Como você já usou uma fórmula para encontrar o termo que falta, a parte mais difícil já está feita. Tudo o que você precisa fazer é colocar o x e a metade do segundo coeficiente entre parênteses e elevá-lo ao quadrado, assim: (x + 2/3). Observe que fatorar o quadrado resulta em 3 termos: x + 4/3 x + 4/9. A equação agora fica assim: (x + 2/3) = 7/9.

8. Tire a raiz quadrada de ambos os lados da equação. No lado esquerdo da equação, a raiz quadrada de (x + 2/3) é igual a x + 2/3. O lado direito dá +/- (√7)/3. A raiz quadrada do denominador 9 é 3, e a raiz quadrada de 7 é √7. Não se esqueça de escrever o +/- porque a raiz quadrada de um número pode ser positiva ou negativa.

9. Deixe a variável de lado. Para isolar a variável x do resto, mova a constante 2/3 para o lado direito da equação. Agora você tem duas respostas possíveis para x:+/- (√7)/3 - 2/3. Estas são suas duas respostas. Você pode deixar assim ou elaborar sobre a raiz quadrada, se for solicitada uma resposta sem radical.
Pontas
- Certifique-se de colocar o +/- nos lugares certos, caso contrário você receberá apenas uma resposta.
- Mesmo que você conheça a fórmula da raiz quadrada, não faz mal praticar a divisão de quadrados ou trabalhar com equações do segundo grau de vez em quando. Assim você tem a certeza de que sabe como fazer quando for necessário.
Artigos sobre o tópico "Quadrado dividido"
Оцените, пожалуйста статью
Popular