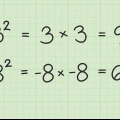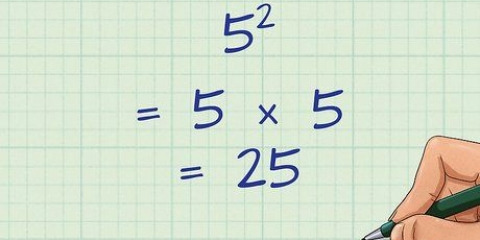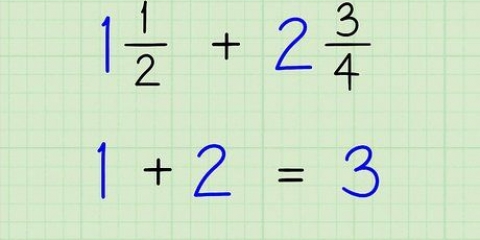30√2 - 4√2 + 10√3 = (30 - 4)√2 + 10√3 = 26√2 + 10√3 

Simplificar 6√(40). Primeiro você pode dissolver `40` em `4 x 10`, e você obtém 6√(40) = 6√(4×10). Então você calcula `2` a partir do quadrado `4` e multiplica isso pelo coeficiente atual. Agora você tem 6√(4×10) = (6 x 2)√10. Multiplique os dois coeficientes e você terá 12√10`.` A tarefa agora é a seguinte: 12√10 - 3√(10) + √5. Como os dois primeiros termos têm a mesma raiz, você pode subtrair o segundo termo do primeiro e deixar o terceiro como está. você ama agora (12-3)√10 + √5 sobre, que pode ser simplificado para 9√10 + √5. 

Porque √9 é igual a √(3x3), você pode simplificar isso: √9 está se tornando 3. Porque √4 é igual a √(2x2), você pode simplificar isso: √4 torna-se 2. Agora a soma 3 + 2 = 5. Porque 5 e 3√2 não são termos iguais, não há mais nada a fazer agora. Sua resposta final é 5 - 3√2. 
Certifique-se de que esses termos tenham o mesmo denominador. O mínimo denominador comum ou denominador divisível por `4` e `2` é `4`. Então, para fazer o segundo termo ((√2)/2) com um denominador 4, você precisa multiplicar o numerador e o denominador por 2/2. (√2)/2 x 2/2 = (2√2)/4. Some o denominador das frações mantendo o denominador o mesmo. Apenas faça o que você faria se estivesse adicionando frações. (√2)/4 + (2√2)/4 = 3√2)/4`.`
Adicionar e subtrair raízes quadradas
Para adicionar e subtrair raízes quadradas, você deve combinar raízes quadradas com a mesma raiz. Isso significa que você pode somar (ou subtrair) 2√3 a 4√3, mas não pode somar 2√3 e 2√5. Existem muitos casos em que você pode simplificar o número sob o radical para poder combinar termos semelhantes e adicionar e subtrair raízes quadradas livremente.
Degraus
Parte 1 de 2: Dominando o básico

1. Simplifique os termos sob os radicais se possível. Para simplificar os termos sob os radicais, tente fatorá-los em pelo menos um quadrado perfeito, como 25 (5 x 5) ou 9 (3 x 3). Depois de fazer isso, você pode tirar a raiz quadrada do quadrado perfeito e colocá-lo fora dos radicais, deixando o fator restante abaixo do radical. Neste exemplo partimos do problema 6√50 - 2√8 + 5√12. Os números fora do radical são os coeficientes e os números abaixo dele chamamos de números de raiz. Veja como simplificar os termos:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Você dissolveu `50` em `25 x 2` e então colocou `5` fora da raiz (a raiz de `25`), após o que `2` permanece abaixo do radical. Então você multiplica `5` por `6`, o número que já estava fora do radical, e você obtém 30 como o novo coeficiente.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Aqui você fatorou `8` em `4 x 2` e então subtraiu a raiz quadrada de 4 para que você fique com `2` fora do radical e um `2` abaixo do radical. Então você multiplica `2` por `2`, o número que já estava fora do radical, e obtém 4 como o novo coeficiente.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Aqui você fatorou `12` em `4 x 3` e então subtraiu a raiz quadrada de 4 para que você fique com `2` fora do radical e um `3` abaixo do radical. Então você multiplica `2` por `5`, o número que já estava fora do radical, e você obtém 10 como o novo coeficiente.

2. Circule quaisquer termos com números de raiz correspondentes. Depois de simplificar os números de raiz dos termos fornecidos, você fica com a seguinte equação: 30√2 - 4√2 + 10√3. Como você só pode adicionar ou subtrair raízes semelhantes, você deve circular esses termos com a mesma raiz, neste exemplo: 30√2 e 4√2. Você pode comparar isso com a adição ou subtração de frações, onde você só pode adicionar ou subtrair os termos se os denominadores forem iguais.

3. Se você estiver trabalhando com uma equação mais longa e houver vários pares de números de raiz correspondentes, você pode circular o primeiro par, sublinhar o segundo, asterisco no terceiro e assim por diante. Colocar os termos semelhantes em ordem facilitará a visualização da solução.

4. Calcule a soma dos coeficientes dos termos com raízes iguais. Agora tudo o que você precisa fazer é calcular a soma dos coeficientes dos termos com raízes iguais, ignorando os outros termos da equação. Os números de raiz permanecem inalterados. A ideia é que você indique quantos desse tipo de número raiz existem, no total. Os termos incompatíveis podem permanecer como estão. Aqui está o que você faz:
Parte 2 de 2: Mais exercícios

1. Faça o exemplo 1. Neste exemplo, você adiciona as seguintes raízes quadradas: √(45) + 4√5. Você deve fazer o seguinte:
- Simplificar (45). Primeiro você pode desvinculá-lo assim √(9 x 5).
- Então você pega a raiz quadrada de nove e obtém `3`, que você coloca fora da raiz quadrada. assim, √(45) = 3√5.
- Agora adicione os coeficientes dos dois termos com raízes correspondentes para obter sua resposta. 3√5 + 4√5 = 7√5

2. Faça o exemplo 2. O exemplo a seguir é esta atribuição: 6√(40) - 3√(10) + √5. Você precisa fazer o seguinte para corrigir isso:
3. Faça o exemplo 3. Este exemplo fica assim: 9√5 -2√3 - 4√5. Nenhuma das raízes contém um quadrado, então nenhuma simplificação é possível. O primeiro e o terceiro termos têm raízes iguais, então seus coeficientes podem ser subtraídos (9 - 4). O número raiz permanece o mesmo. Os termos restantes não são iguais, então o problema pode ser simplificado para5√5 - 2√3`.`


4. Faça o exemplo 4. Suponha que você esteja lidando com o seguinte problema: √9 + √4 - 3√2 Agora você precisa fazer o seguinte:

5. Faça o exemplo 5. Vamos tentar fazer a soma das raízes quadradas que fazem parte de uma fração. Assim como uma fração regular, agora você só pode calcular a soma das frações com o mesmo numerador ou denominador. Digamos que você esteja trabalhando com este problema: (√2)/4 + (√2)/2, Agora faça o seguinte:
Pontas
- Números de raiz com um quadrado como fator devem sempre ser simplificados por você vai determinar e combinar números de raiz iguais.
Avisos
- Você nunca pode combinar números de raiz desiguais.
- Você nunca pode combinar um número inteiro e uma raiz quadrada. Assim: 3 + (2x) posso não ser simplificado.
- Observação: `(2x) é o mesmo que `(√(2x)`.
Artigos sobre o tópico "Adicionar e subtrair raízes quadradas"
Оцените, пожалуйста статью
Popular