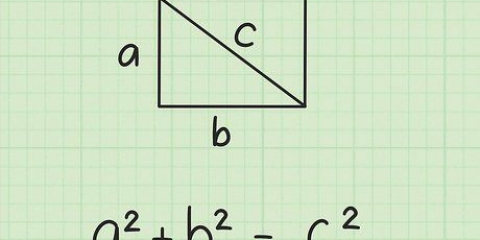
Esta fórmula é derivada do teorema de Pitágoras ( . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para encontrar o comprimento da diagonal (que é a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para encontrar o comprimento da diagonal (que é a hipotenusa do triângulo retângulo). 
Por exemplo, se os lados do quadrado tiverem um comprimento de 5 centímetros cada, a fórmula ficaria assim:


Por exemplo, se você calcular a diagonal de um quadrado de 5 centímetros, sua fórmula ficará assim:


Então, a diagonal do quadrado tem 7,07 centímetros de comprimento. 

Por exemplo, se o perímetro do quadrado for 20 centímetros, sua fórmula ficaria assim:


Por exemplo:




Esta fórmula é derivada do teorema de Pitágoras ( . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, assim, você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, assim, você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo). 
Por exemplo, se o quadrado tiver um comprimento de 5 centímetros, a fórmula ficaria assim:


Por exemplo, se você calcular a diagonal de um quadrado de 5 centímetros, sua fórmula ficaria assim:


Então, a diagonal do quadrado tem 7,07 centímetros de comprimento. 

Por exemplo, se a área do quadrado for 25 centímetros quadrados, sua fórmula ficaria assim:


Por exemplo:




Esta fórmula é derivada do teorema de Pitágoras ( . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo). 
Por exemplo, se o quadrado tiver um comprimento de 5 centímetros, a fórmula ficaria assim:


Por exemplo, se você calcular a diagonal de um quadrado de 5 centímetros, sua fórmula ficaria assim:


Então, a diagonal do quadrado é 7,07 centímetros.
Calculando a diagonal de um quadrado
Contente
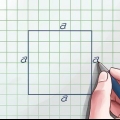
A diagonal de um quadrado é a linha de um canto desse quadrado até o canto oposto. Para encontrar a diagonal de um quadrado, use a fórmula 

Degraus
Método 1 de 3: Se você souber o comprimento de um lado

1. Encontre o comprimento de um lado do quadrado. Isso provavelmente é dado. Se você estiver lidando com um quadrado no mundo real, use uma régua ou fita métrica para determinar seu comprimento. Como todos os quatro lados do quadrado têm o mesmo comprimento, você pode usar qualquer lado do quadrado. Se você não conhece os lados do quadrado, não pode usar este método.
- Por exemplo, encontre o comprimento da diagonal de um quadrado com lados de 5 centímetros.

2. Anote a fórmula: . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e
igual ao comprimento da diagonal e  igual a um lado do quadrado.
igual a um lado do quadrado.
 . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e
igual ao comprimento da diagonal e  igual a um lado do quadrado.
igual a um lado do quadrado. . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para encontrar o comprimento da diagonal (que é a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para encontrar o comprimento da diagonal (que é a hipotenusa do triângulo retângulo).
3. Digite o comprimento do lado do quadrado na fórmula. Certifique-se de substituir a variável  .
.
 .
.

4. Multiplique o comprimento do lado por 2  . Isso dá o comprimento da diagonal. Este cálculo é feito melhor com uma calculadora, para que a resposta seja mais precisa. Não tem calculadora, redondo
. Isso dá o comprimento da diagonal. Este cálculo é feito melhor com uma calculadora, para que a resposta seja mais precisa. Não tem calculadora, redondo  depois para 1.414.
depois para 1.414.
 . Isso dá o comprimento da diagonal. Este cálculo é feito melhor com uma calculadora, para que a resposta seja mais precisa. Não tem calculadora, redondo
. Isso dá o comprimento da diagonal. Este cálculo é feito melhor com uma calculadora, para que a resposta seja mais precisa. Não tem calculadora, redondo  depois para 1.414.
depois para 1.414.

Então, a diagonal do quadrado tem 7,07 centímetros de comprimento.
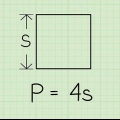
Método 2 de 3: Quando o perímetro é dado

1. Escreva a fórmula do perímetro de um quadrado. A fórmula é  , através do qual
, através do qual  é igual ao perímetro do quadrado, e
é igual ao perímetro do quadrado, e  igual ao comprimento de um lado do quadrado.
igual ao comprimento de um lado do quadrado.
 , através do qual
, através do qual  é igual ao perímetro do quadrado, e
é igual ao perímetro do quadrado, e  igual ao comprimento de um lado do quadrado.
igual ao comprimento de um lado do quadrado. - Este método só funciona se o perímetro do quadrado for dado.
- Para encontrar o comprimento da diagonal, primeiro você precisa encontrar o comprimento de um lado do quadrado, então você precisa usar a fórmula para o perímetro e
resolver.

2. Insira o comprimento da circunferência na fórmula. Certifique-se de preencher para a variável  .
.
 .
.

3. Resolva para s  . Para fazer isso, divida cada lado da equação por 4. Isso lhe dará o comprimento de um lado do quadrado.
. Para fazer isso, divida cada lado da equação por 4. Isso lhe dará o comprimento de um lado do quadrado.
 . Para fazer isso, divida cada lado da equação por 4. Isso lhe dará o comprimento de um lado do quadrado.
. Para fazer isso, divida cada lado da equação por 4. Isso lhe dará o comprimento de um lado do quadrado.



4. Escreva a fórmula d = s 2  . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e
igual ao comprimento da diagonal e  igual a um lado do quadrado.
igual a um lado do quadrado.
 . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e
igual ao comprimento da diagonal e  igual a um lado do quadrado.
igual a um lado do quadrado. . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, assim, você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, assim, você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
5. Insira o comprimento do lado do quadrado na fórmula. Certifique-se de substituir a variável  .
.
 .
.

6. Multiplique o comprimento do lado por 2  . Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima
. Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima  desligado em 1.414.
desligado em 1.414.
 . Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima
. Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima  desligado em 1.414.
desligado em 1.414.

Então, a diagonal do quadrado tem 7,07 centímetros de comprimento.
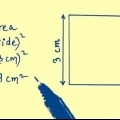
Método 3 de 3: Quando a área é dada

1. Escreva a formula da area de um quadrado. A fórmula é  , através do qual
, através do qual  é igual à área do quadrado, e
é igual à área do quadrado, e  igual ao comprimento de um lado do quadrado.
igual ao comprimento de um lado do quadrado.
 , através do qual
, através do qual  é igual à área do quadrado, e
é igual à área do quadrado, e  igual ao comprimento de um lado do quadrado.
igual ao comprimento de um lado do quadrado. - Este método só funciona se a área do quadrado for conhecida.
- Para encontrar o comprimento da diagonal, você deve primeiro determinar o comprimento de um lado do quadrado, a razão pela qual você deve primeiro usar a fórmula da área e
resolver.

2. Substitua o valor da área na fórmula. Certifique-se de substituir a variável  .
.
 .
.

3. Resolva para s  . Você faz isso determinando a raiz quadrada da área. Isso lhe dará o comprimento de um lado do quadrado. Agora determine a raiz quadrada com uma calculadora. Se precisar de ajuda para calcular a raiz quadrada manualmente, leia Calcular a raiz quadrada de um número sem calculadora.
. Você faz isso determinando a raiz quadrada da área. Isso lhe dará o comprimento de um lado do quadrado. Agora determine a raiz quadrada com uma calculadora. Se precisar de ajuda para calcular a raiz quadrada manualmente, leia Calcular a raiz quadrada de um número sem calculadora.
 . Você faz isso determinando a raiz quadrada da área. Isso lhe dará o comprimento de um lado do quadrado. Agora determine a raiz quadrada com uma calculadora. Se precisar de ajuda para calcular a raiz quadrada manualmente, leia Calcular a raiz quadrada de um número sem calculadora.
. Você faz isso determinando a raiz quadrada da área. Isso lhe dará o comprimento de um lado do quadrado. Agora determine a raiz quadrada com uma calculadora. Se precisar de ajuda para calcular a raiz quadrada manualmente, leia Calcular a raiz quadrada de um número sem calculadora.



4. Escreva a fórmula d = s 2  . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e é
igual ao comprimento da diagonal e é  igual a um lado do quadrado.
igual a um lado do quadrado.
 . Na fórmula . é
. Na fórmula . é  igual ao comprimento da diagonal e é
igual ao comprimento da diagonal e é  igual a um lado do quadrado.
igual a um lado do quadrado. . Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
. Uma diagonal divide um quadrado em dois triângulos retângulos congruentes, então você pode usar os comprimentos dos lados do quadrado para determinar o comprimento da diagonal (a hipotenusa do triângulo retângulo).
5. Use o comprimento do lado do quadrado na fórmula. Certifique-se de substituir a variável  .
.
 .
.

6. Multiplique o comprimento do lado por 2  . Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima
. Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima  desligado em 1.414.
desligado em 1.414.
 . Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima
. Isso lhe dará o comprimento da diagonal. É melhor fazer esse cálculo com uma calculadora, para obter um resultado mais preciso. Se você não tiver uma calculadora, arredonde para cima  desligado em 1.414.
desligado em 1.414.

Então, a diagonal do quadrado é 7,07 centímetros.
Necessidades
- Calculadora
Artigos sobre o tópico "Calculando a diagonal de um quadrado"
Оцените, пожалуйста статью
Similar
Popular