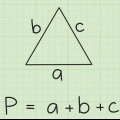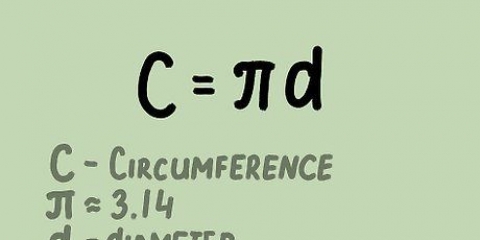Como Calcular a Circunferência de um Quadrado

Contente

Degraus

O perímetro de uma figura bidimensional é a distância total em torno da figura, ou a soma dos comprimentos dos lados. A definição de um quadrado é uma figura com quatro lados iguais e quatro ângulos retos (90°) entre esses lados. Como todos os lados têm o mesmo comprimento, é muito fácil determinar o perímetro de um quadrado! Este artigo aborda primeiro como calcular o perímetro de um quadrado se você souber o comprimento de um de seus lados. Em seguida, mostraremos como calcular o perímetro se você conhecer apenas a área e, na última seção, ensinaremos como calcular o perímetro de um quadrado inscrito em um círculo cujo comprimento do raio é conhecido.

Degraus

Método 1 de 3: Encontrando o perímetro de um quadrado se você souber o comprimento de um lado

Imagem intitulada Calcular o perímetro de um quadrado Passo 1

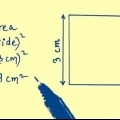
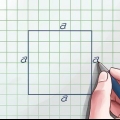
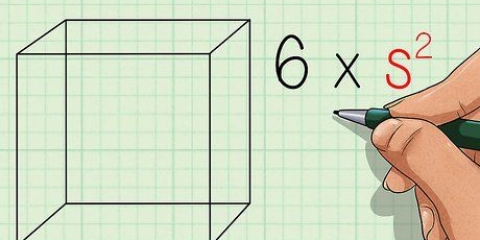
1. Pense na fórmula do perímetro de um quadrado. Para um quadrado onde encontramos o comprimento do lado s o perímetro é simplesmente quatro vezes o comprimento desse lado: Circunferência = 4s (nota: nas imagens a letra P é usada para contorno, do inglês `Perimeter`).

Imagem intitulada Calcule o perímetro de um quadrado Passo 2

2. Encontre o comprimento de um lado e multiplique por 4 para encontrar o perímetro. Dependendo da tarefa, pode ser necessário medir com uma régua ou consultar outras informações para determinar o comprimento de um lado. Aqui estão alguns exemplos de cálculos de circunferência:

Se o quadrado tem um lado de comprimento 4:Circunferência = 4 * 4, em outras palavras 16.

Se o quadrado tem um lado de comprimento 6: Circunferência = 4 * 6, em outras palavras 24.

Método 2 de 3: Determinando o perímetro de um quadrado se você conhece sua área

Imagem intitulada Calcule o perímetro de um quadrado Passo 3

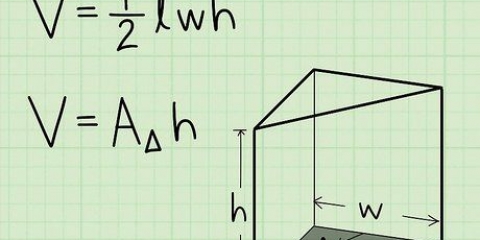
1. Conheça a fórmula da área de um quadrado. A área de qualquer retângulo (lembre-se que os quadrados são retângulos especiais) pode ser definida como base vezes altura.Como a base e a altura são iguais no caso de um quadrado, a área de um quadrado de lado s: s*s. Em outras palavras: área = s.

Imagem intitulada Calcular o perímetro de um quadrado Passo 4

2. Tire a raiz quadrada da área. A raiz quadrada da área dá-lhe o comprimento de um dos lados do quadrado. Para a maioria dos números, você precisa de uma calculadora para calcular a raiz quadrada. Digite o número primeiro e, em seguida, pressione a tecla de raiz quadrada (√).

Se a área do quadrado é 20, então o comprimento do lado é s: =√20 ou 4.472

Se a área do quadrado é 25, então o comprimento do lado é s = √25 ou 5.

Imagem intitulada Calcular o perímetro de um quadrado Passo 5

3. Multiplique o comprimento do lado por 4 para encontrar a circunferência. Use o valor do comprimento do lado que você acabou de encontrar na fórmula Circunferência = 4s. O resultado é o perímetro do seu quadrado!

Para um quadrado com área de 20 e comprimento de lado de 4,473, o perímetro é: Circunferência = 4 * 4,472 ou 17.888.

Para um quadrado com área de 25 e comprimento de lado de 5, o perímetro é: Circunferência = 4 * 5 ou 20.

Método 3 de 3: Calculando o perímetro de um quadrado inscrito em um círculo se você souber o raio

Imagem intitulada Calcular o perímetro de um quadrado Passo 6

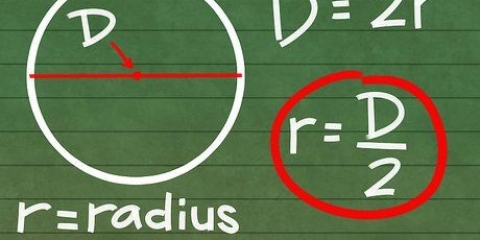
1. Entenda o que é um quadrado inscrito. Um quadrado inscrito em um círculo é um quadrado desenhado em um círculo com todos os cantos do quadrado tocando o círculo.

Imagem intitulada Calcular o perímetro de um quadrado Passo 7

2. Entenda a relação entre o raio do círculo e o comprimento dos lados do quadrado. A distância do centro de um quadrado inscrito a qualquer canto é igual ao raio do círculo. Para o comprimento lateral s para encontrar, devemos primeiro imaginar que cortamos o quadrado ao meio na diagonal, de modo que dois triângulos equiláteros são formados. Esses triângulos têm lados iguais uma e b e uma hipotenusa c, que sabemos é igual a duas vezes o raio do círculo, ou seja, 2º lugar.

Imagem intitulada Calcular o perímetro de um quadrado Passo 8

3. Use o teorema de Pitágoras para encontrar o comprimento do lado do quadrado. O teorema de Pitágoras é o seguinte: em um triângulo retângulo, a soma dos quadrados dos comprimentos dos lados retangulares (a,b) é igual ao quadrado do comprimento da hipotenusa (c), a + b = c. Porque os lados uma e b são iguais (ainda estamos lidando com um quadrado!) e sabemos que c=2r agora podemos escrever a equação e simplificá-la para encontrar o comprimento de um lado:

a + a = (2r), agora podemos simplificar:

2a = 4(r), agora divida ambos os lados por 2:

(a) = 2(r), agora tire a raiz quadrada de cada lado:

a = √(2)r.Nosso comprimento de um lado s do quadrado inscrito = √(2)r.

Imagem intitulada Calcular o perímetro de um quadrado Passo 9

4. Multiplique o comprimento de um lado do quadrado por quatro para encontrar o perímetro. Neste caso, o perímetro do quadrado é: Circunferência = 4√(2)r. A circunferência de um quadrado inscrito em um círculo é, portanto, sempre igual a 4√(2)r, ou cerca de 5,657r

Imagem intitulada Calcular o perímetro de um quadrado Passo 10

5. Resolver uma pergunta de exemplo. Tomamos um quadrado inscrito em um círculo com um raio de 10. Isso significa que a diagonal do quadrado = 2(10) ou 20. O teorema de Pitágoras nos ensina que: 2(a) = 20, assim 2a = 400. Agora divida ambos os lados por dois, vemos que a = 200. Tire a raiz quadrada de cada lado e vemos que a = 14,142. Multiplique isso por 4 para encontrar o perímetro do seu quadrado: Circunferência = 56,57.

Nota: você também poderia ter feito assim: multiplique o raio (10) pelo número 5.567. 10*5.567 = 56.57, mas porque isso pode ser difícil de lembrar, é melhor você passar por todo o processo.