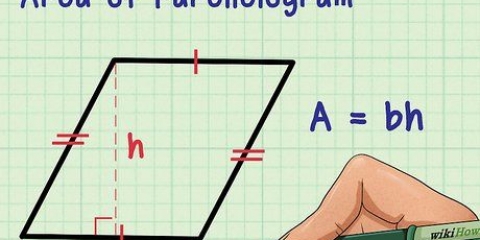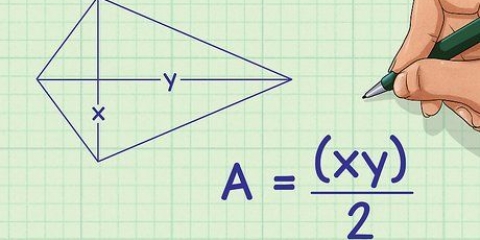Para formas pequenas, você pode usar centímetros, enquanto metros ou quilômetros são mais adequados para circunferências maiores. Quando os lados opostos dos retângulos são iguais, você só precisa medir um dos lados opostos. 
Continue com o exemplo: imagine que além de um comprimento de 3 cm, a largura do seu retângulo é de 5 cm. 

Então, neste exemplo, você calcula 3 + 3 + 5 + 5 = 16 (o perímetro). Você também pode usar a fórmula 2 x (comprimento + largura) para retângulos, pois o comprimento e a largura dos lados opostos são iguais e, portanto, dobrados. Então, em nosso exemplo, isso é: 2 x 8 = 16. 
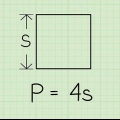
Quadrado: comprimento de cada lado x 4 Triângulo: somar todos os lados Polígono irregular: somar todos os lados Círculo: 2 x π x raio ou π x diâmetro. O símbolo π significa Pi (pronuncia-se torta). Se você tiver uma tecla π em sua calculadora, poderá usá-la para ser mais preciso ao usar esta fórmula. Caso contrário, você pode arredondar o valor de π para 3,14. O termo `raio` refere-se à distância entre o centro de um círculo e seu limite externo (circunferência), enquanto `diâmetro` refere-se ao comprimento de uma linha imaginária entre dois pontos opostos na circunferência de um círculo que passa pelo centro de o círculo. o círculo vai. 

Você pode dividir a forma em segmentos verticais e horizontais de uma unidade (cm, m) se quiser visualizar como será a medição da área. 
Você pode escrever `unidades quadradas/unidades quadradas` como: cm² m² km² 
Paralelogramo: base x altura Quadrado: lado 1 x lado 2 Triângulo: ½ x base x altura. Alguns matemáticos usam a notação: A = ½ bh. Círculo: π x r² (onde r = raio) O termo "raio" refere-se à distância entre o centro de um círculo e seu limite externo (circunferência), e os dois pequenos em sobrescrito (o quadrado) indicam que o valor ao qual os dois pertencem é multiplicado por ele mesmo.
Determine a área e o perímetro
Contente
O perímetro é o comprimento de todo o limite externo de uma figura plana (bidimensional), e a área é a medida de seu tamanho. Área e perímetro são medidas extremamente úteis que podem ser usadas em projetos domésticos, construção, projetos de bricolage e ao estimar a quantidade de materiais que você pode precisar. Por exemplo, se você quiser pintar um quarto, precisará saber quanta tinta precisa ou, em outras palavras, quanto superfície a tinta pode cobrir. O mesmo pode ser dito ao organizar um jardim, construir uma cerca ou fazer várias outras tarefas em casa. Nessas situações, você pode usar área e perímetro para economizar tempo e dinheiro na compra de materiais.
Degraus
Parte 1 de 2: Determinando a circunferência

1. Determine a forma que você deseja medir. O perímetro é o limite externo em torno de uma figura geométrica fechada, e formas diferentes exigirão abordagens diferentes. Se a forma cujo perímetro você deseja encontrar não for uma forma fechada, o perímetro não pode ser determinado.
- Se esta é sua primeira vez calculando o perímetro, tente um retângulo ou um quadrado. Essas formas regulares facilitam a determinação do perímetro.

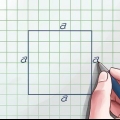
2. Desenhe um retângulo em um pedaço de papel. Você usa este retângulo como uma forma prática e determina seu perímetro. Certifique-se de que os lados opostos do retângulo tenham o mesmo comprimento.

3. Determine o comprimento de um lado do seu retângulo. Você pode fazer isso com uma régua, fita métrica ou inventando seu próprio exemplo. Escreva este número ao lado do lado que ele representa, para não esquecer o comprimento. Suponha que o comprimento de um lado do seu retângulo seja 3 cm.

4. Determine a largura de um lado do seu retângulo. Você pode medir a largura com uma régua, fita métrica ou fazendo seu próprio exemplo. Escreva o valor da sua largura ao lado do lado horizontal do retângulo que ele representa.

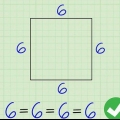
5. Escreva as medidas corretas nos lados opostos do seu retângulo. Os retângulos têm quatro lados, mas o comprimento dos lados opostos será o mesmo. Isso também se aplica à largura do seu retângulo. Escreva o comprimento e a largura usados no exemplo (3 e 5 cm respectivamente) nos lados opostos do retângulo.

6. Junte todos os lados. Sob o exemplo que você fez ou anotou, escreva o seguinte: comprimento + comprimento + largura + largura.

7. Ajuste sua abordagem para diferentes formas. Infelizmente, formas diferentes exigirão fórmulas diferentes para o perímetro. Em exemplos do mundo real, você pode medir o limite externo de qualquer forma geométrica fechada para determinar seu perímetro. Mas você também pode usar as seguintes fórmulas para encontrar o perímetro de outras formas comuns:
Parte 2 de 2: Determinando a área

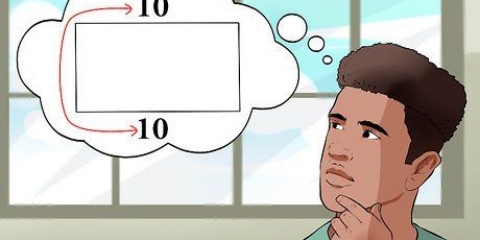
1. Determine as dimensões da sua forma. Desenhe um retângulo ou use o mesmo retângulo que você desenhou ao determinar o perímetro. Neste exemplo, você está calculando a área de um retângulo, usando sua altura e largura.
- Você pode trabalhar com uma régua ou fita métrica ou criar seu próprio exemplo. Neste exemplo, o comprimento e a largura são iguais ao exemplo anterior usado para encontrar o perímetro: 3 e 5 . respectivamente.

2. Entenda o verdadeiro significado da superfície. Determinar a área dentro de um perímetro é como dividir esse espaço vazio dentro de sua forma em quadrados de 1 por 1. A área pode ser menor ou maior que o perímetro, dependendo da forma.

3. Multiplique o comprimento do seu retângulo pela largura. No exemplo: área = 3 x 5, que é 15 metros quadrados. A unidade de medida para a área deve sempre ser escrita em unidades quadradas (km quadrados, metros quadrados, etc.).).

4. Altere sua fórmula dependendo da forma. Infelizmente, diferentes formas geométricas exigirão uma abordagem diferente para calcular a área. Você pode usar as seguintes fórmulas para encontrar a área de algumas formas comuns:
Pontas
- Essas fórmulas de área e perímetro só funcionam para a área (o volume) de uma forma plana. Se você precisar encontrar o conteúdo de uma forma tridimensional (o volume), precisará procurar fórmulas para volume, como aquelas para cones, cubos, cilindros, prismas e pirâmides.
Necessidades
- Papel
- Lápis
- Calculadora (opcional)
- Fita métrica (opcional)
- Régua (opcional)
Artigos sobre o tópico "Determine a área e o perímetro"
Оцените, пожалуйста статью
Similar
Popular