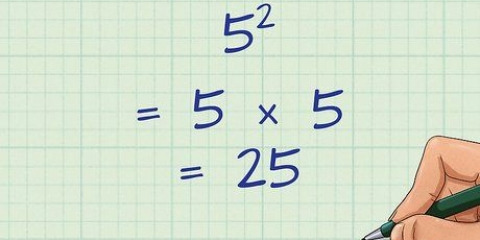Outro exemplo: Queremos encontrar a raiz quadrada de 25 (√(25)). Isso significa que precisamos encontrar o número que multiplicado por ele mesmo tem 25 como produto. Como 5 = 5 × 5 = 25, podemos dizer que √(25) = 5. Você também pode pensar nisso como "desfazer" um quadrado (ou número de potência). Por exemplo, se quisermos encontrar a raiz quadrada de 64 (√64), considere 64 como 8. primeiro. Como um radical em princípio `elimina` um quadrado, podemos dizer que √(64) = √(8) = 8. 
Por outro lado, os números que não dão números inteiros após a raiz quadrada são chamados, quadrado imperfeito. Quando você tira a raiz quadrada de um desses números, geralmente obtém um decimal ou fração. Às vezes, os decimais envolvidos podem ficar muito confusos. Por exemplo, √(13) = 3.605551275464… 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Suponha que você queira calcular a raiz quadrada de 900. À primeira vista, isso parece muito difícil! No entanto, não é difícil se fatorarmos 900. `Fatores` são aqueles números que podem se multiplicar para formar outro número. Por exemplo, como 6 é o produto de 1 × 6 e 2 × 3, os fatores de 6 são os números 1, 2, 3 e 6. Em vez de calcular com o número 900, que é um pouco inconveniente, escrevemos como 9 × 100. Agora, como 9 é um quadrado perfeito e separado de 100, podemos tirar sua raiz quadrada. √(9 × 100) = √(9) × √(100) = 3 × √(100). Em outras palavras, √(900) = 3√(100). Podemos simplificar ainda mais esses dois passos dividindo 100 nos fatores 25 e 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Então podemos dizer que √(900) = 3(10) = 30. 
Nota: Embora os números imaginários não possam ser representados com números regulares, eles ainda podem ser tratados como números regulares de várias maneiras. Por exemplo, as raízes de números negativos podem ser elevadas ao quadrado para dar esses números negativos como qualquer outra raiz quadrada. Por exemplo: i = -1. 

Em nosso exemplo, dividimos 6,45 em pares assim: 6-,45-00. Observe que há um número `restante` à esquerda &mdash esse é o ponto. 
Em nosso exemplo, o primeiro grupo em 6-,45-00 é o 6. O maior número menor ou igual a 6 é 2 — 2 = 4. Escreva um `2` acima do 6 abaixo do radical. 
Em nosso exemplo, começaremos com o dobro de 2, o primeiro dígito de nossa resposta. 2 × 2 = 4. Então subtraímos 4 de 6 (nosso primeiro `grupo`) e obtemos 2 como resposta. Em seguida, movemos o próximo grupo (45) para baixo uma linha para obter 245. Por fim, escreveremos outros 4 à esquerda, deixando um pouco de espaço para adicionar no final, assim: 4_. 
Em nosso exemplo, estamos procurando o número para preencher o espaço em branco em 4_ × _; que torna a resposta o maior possível, mas ainda menor ou igual a 245. Neste caso a resposta é 5. 45 × 5 = 225, enquanto 46 × 6 = 276. 
Continuamos com nosso exemplo e continuamos com 225 - 245 = 20. Então abaixamos o próximo par de dígitos, 00, para fazer 2000. Se dobrarmos o número acima do radical, obtemos 25 × 2 = 50. Resolvemos a incógnita em 50_ × _ =/< 2000, então temos 3 como resposta. Neste ponto, temos `253` acima do radical - repetindo isso novamente, 9 é o próximo dígito. 
Em nosso exemplo, o número sob o sinal do radical é 6,45, então simplesmente movemos a vírgula para cima e a colocamos entre 2 e 5 de nossa resposta, o que nos dá 2.539 rendimentos. 

Em nosso problema de exemplo, uma estimativa razoável para a raiz quadrada de 40 talvez seja 6.4, porque pelo que foi dito acima sabemos que a resposta é provavelmente um pouco mais próxima de 6 do que de 7. 
Multiplique 6,4 por ele mesmo, então 6,4 × 6,4 = 40,96, que é um pouco maior que o número original. Em seguida, multiplicamos o número por um décimo menor do que nossa estimativa acima (porque nossa resposta foi muito alta) e obtemos 6,3 × 6,3 = 39,69. Este é um pouco menor do que o nosso número original. Isso significa que a raiz quadrada de 40 está em algum lugar entre 6,3 e 6,4 mentiras. Além disso, como 39,69 está mais próximo de 40 do que 40,96, você sabe que a raiz quadrada está mais próxima de 6,3 do que de 6,4. 
Em nosso exemplo, vamos escolher 6,33 para nosso palpite em duas casas decimais. Quadrado 6,33 e você obtém 6,33 × 6,33 = 40,0689. Como isso está um pouco acima do nosso número original, tentaremos um número um pouco menor, como 6,32. 6,32 × 6,32 = 39,9424. Isso está um pouco abaixo do nosso número original, então sabemos que a raiz quadrada exata entre 6,33 e 6,32 mentiras. Se quiséssemos ir mais longe, podemos continuar a usar a mesma abordagem para obter uma resposta cada vez mais precisa.
Resolver raízes quadradas
Contente
Embora a visão intimidante de um símbolo de raiz quadrada possa fazer as pessoas com ansiedade matemática se encolherem, os problemas de raiz quadrada não são tão difíceis de resolver quanto parecem à primeira vista. Problemas simples de raiz quadrada geralmente podem ser resolvidos tão facilmente quanto problemas simples de multiplicação e divisão. Problemas de raiz quadrada mais complexos, por outro lado, podem exigir um pouco mais de trabalho, mas com a abordagem correta, mesmo esses problemas podem ser resolvidos facilmente. Comece a praticar problemas de raiz quadrada hoje para aprender essa habilidade matemática que pode ser nova para você!
Degraus
Parte 1 de 3: Entendendo Poderes e Raízes

1. Eleve ao quadrado um número multiplicando-o por ele mesmo. Para entender as raízes, é melhor começar com os quadrados. Quadrados são fáceis — elevar ao quadrado um número equivale a multiplicá-lo por ele mesmo. Por exemplo: 3 ao quadrado é o mesmo que 3 × 3 = 9, e 9 ao quadrado é o mesmo que 9 × 9 = 81. Os quadrados são indicados por um pequeno "2" acima e à direita do número ao quadrado - assim: 3, 9, 100, etc.
- Tente quadrar alguns números você mesmo para testar esse conceito. Lembre-se que elevar ao quadrado um número nada mais é do que multiplicar esse número por ele mesmo. Você pode fazer isso mesmo com números negativos. Em todos os casos, a resposta será sempre positiva. Por exemplo: -8 = -8 × -8 = 64.

2. Para encontrar a raiz de um número, encontre o `inverso de` um quadrado. O símbolo da raiz quadrada (√, também conhecido como `sinal radical`) é basicamente o `oposto` do símbolo quadrado (). Se você vir um sinal de radical, poderá se perguntar: `Qual número posso multiplicar por si mesmo para obter o número sob o sinal de radical??` Por exemplo: se você vir a raiz quadrada √(9), então você está procurando o número que multiplicado por ele mesmo tem nove como produto. Neste caso é isso três, porque 3 = 9.

3. Saiba a diferença entre quadrados perfeitos e imperfeitos. Até agora, as respostas para os problemas de raiz quadrada eram bons, números redondos. Isso nem sempre é o caso - na verdade, existem respostas para raízes quadradas que são números decimais muito longos e estranhos. Números raiz que são números inteiros (em outras palavras, números que não são fracionários ou decimais) são chamados quadrados. Todos os exemplos acima (9, 25 e 64) são quadrados (também chamados de quadrados perfeitos), porque, ao extrair raízes quadradas, obtemos números inteiros (3, 5 e 8) como resultado.

4. Memorize os primeiros 10-12 quadrados. Como você deve ter notado, raízes quadradas ou quadrados costumam ser muito fáceis! Como esses problemas de matemática são tão simples, vale a pena aprender as raízes dos primeiros 12 ou mais quadrados. Você encontrará muito esses números, então você pode economizar muito tempo a longo prazo aprendendo-os cedo. Os primeiros 12 quadrados são:

5. Simplifique as raízes removendo os quadrados sempre que possível. Encontrar as raízes de quadrados imperfeitos às vezes pode ser complicado - especialmente se você não usar uma calculadora (os parágrafos abaixo fornecem truques para facilitar esse processo). No entanto, muitas vezes é possível simplificar os números sob o sinal de radical, para facilitar o trabalho com eles. Para fazer isso, você só precisa fatorar o número sob o radical, depois tirar a raiz quadrada dos fatores que são quadrados e escrever a resposta fora do radical. Isso é mais fácil do que parece - continue lendo para saber mais!

6. Use números imaginários para as raízes de números negativos. Que quadrado é -16? Não é 4 ou -4 — ao quadrado ambos dá 16 (positivo). Você não sabe? Na verdade, não há como escrever a raiz quadrada de -16 ou qualquer número negativo com números regulares. Nesses casos, precisamos usar números imaginários (geralmente na forma de letras ou símbolos) para substituir a raiz quadrada do número negativo. Por exemplo, a variável `i` geralmente é usada para a raiz quadrada de -1. Como regra geral, a raiz quadrada de um número negativo sempre será um número imaginário (ou conterá um).
Parte 2 de 3: Usando algoritmos de divisão longa

1. Ordene seu problema de raiz quadrada como divisão longa. Embora possa ser um pouco demorado, é possível calcular as raízes de quadrados imperfeitos difíceis sem uma calculadora. Para fazer isso, usamos um método de solução (ou algoritmo) que é semelhante a — mas não exatamente igual a — uma longa divisão.
- Primeiro escreva a raiz quadrada da mesma forma que a divisão longa. Por exemplo, digamos que queremos calcular a raiz quadrada de 6,45, que certamente não é um quadrado perfeito conveniente. Primeiro escrevemos um símbolo radical comum (√), depois escrevemos o número abaixo dele. Em seguida, desenhamos uma linha acima do número para que fique em uma pequena `caixa` - assim como a divisão longa. Quando terminamos, notamos um `√` alongado com 6,45 abaixo dele.
- Escrevemos números acima do problema, então deixe algum espaço.

2. Agrupe os números em pares. Para resolver seu problema, agrupe os dígitos do número sob o sinal do radical em pares, começando do ponto decimal. Você pode adicionar pequenos destaques (como pontos, barras, vírgulas, etc.).) entre seus pares para diferenciá-los.

3. Encontre o maior número cujo quadrado é menor ou igual ao primeiro `grupo`. Comece com o primeiro número ou par à esquerda. Escolha o maior número com um quadrado menor ou igual ao `grupo`. Por exemplo, se o grupo for 37, você escolheria o 6, porque 6 = 36 (menos de 37), mas 7 = 49 (maior que 37). Escreva este número acima do primeiro grupo. Este é o primeiro dígito da sua resposta.

4. Dobre o número que você acabou de anotar, escreva no primeiro grupo e subtraia. Pegue o primeiro dígito da sua resposta (o número que você acabou de encontrar) e dobre-o. Escreva isso no seu primeiro grupo e subtraia para encontrar a diferença. Coloque o próximo par de números ao lado da resposta abaixo. Finalmente, escreva o último dígito do dobro do primeiro dígito da sua resposta à esquerda, deixando algum espaço ao lado dele.

5. Preencha o espaço vazio. Em seguida, a intenção é adicionar um dígito à direita do número que você escreveu à esquerda. Escolha um número que multiplicado pelo seu novo número produz o maior produto possível, mas é menor ou igual ao número "extraído". Por exemplo, se o seu número `reduzido` for 1700 e o número à esquerda for 40_, você preencheria o espaço em branco com `404` porque 404 × 4 = 1616 (menos de 1700), enquanto 405 × 5 = 2025. O número encontrado nesta etapa é o segundo dígito da sua resposta, então você pode adicioná-lo acima do radical.

6. Continue usando seus números `em branco` para sua resposta. Continue com essa divisão longa modificada até obter zeros ao subtrair o número de `rebaixamento` ou você atingiu a precisão desejada. Quando terminar, os números que você usou para preencher os espaços em branco em cada etapa (mais o primeiro número que você usou) são os dígitos da sua resposta.

7. Mova o ponto decimal do seu `divisor` original para cima. Para arredondar sua resposta, você precisa colocar a vírgula (o ponto decimal) no lugar certo. Felizmente, isso é fácil - tudo o que você precisa fazer é alinhá-lo com o ponto decimal em seu número original. Se o número abaixo do radical for 49,8, mova a vírgula para cima entre os dois números acima de 9 e 8.
Parte 3 de 3: Estimando quadrados imperfeitos rapidamente

1. Encontre quadrados imperfeitos estimando. Depois de memorizar seus quadrados, encontrar as raízes de quadrados imperfeitos fica muito mais fácil. Como você já conhece uma dúzia de quadrados, qualquer número que caia entre dois desses quadrados perfeitos pode ser encontrado estimando entre esses valores. Para começar, encontre os dois quadrados entre os quais seu número está. Em seguida, determine qual desses dois quadrados está mais próximo do número.
- Por exemplo, suponha que precisamos encontrar a raiz quadrada de 40. Uma vez que memorizamos nossos quadrados, podemos dizer que 40 cai entre 6 e 7, ou 36 e 49. Como 40 é maior que 6, sua raiz quadrada será maior que 6, e como é menor que 7, sua raiz quadrada será menor que 7. O número 40 está um pouco mais próximo de 36 do que 49, então a resposta provavelmente será um pouco mais próxima de 6. Nas próximas etapas, tornaremos nossa resposta mais precisa.

2. Estime a raiz quadrada com uma casa decimal. Depois de escolher dois quadrados entre os quais seu número está, é apenas uma questão de estimar até encontrar uma resposta com a qual você esteja satisfeito. Quanto mais longe você for, mais precisa será sua resposta. Para começar, escolha um dez para sua resposta – não precisa estar correto, mas você economizará tempo se usar o bom senso escolhendo um número próximo da resposta correta.

3. Multiplique a estimativa por ela mesma. Então você eleva ao quadrado a estimativa. A menos que você tenha sorte, você provavelmente não receberá seu número original - você acabará um pouco mais alto ou mais baixo. Se sua resposta for muito alta, tente novamente com uma estimativa um pouco menor (e vice-versa se for muito baixa).

4. Continue estimando se necessário. Se você estiver satisfeito com suas respostas, talvez queira usar um de seus primeiros palpites. No entanto, se você quiser uma resposta mais precisa, tudo o que você precisa fazer é escolher uma estimativa para o seu "centésimo" que coloque essa estimativa entre seus dois primeiros. Se você continuar com esse padrão, poderá obter uma resposta em três, quatro ou mais casas decimais - depende apenas de até onde você deseja ir.
Pontas
- Para soluções rápidas, use uma calculadora. A maioria das calculadoras modernas pode calcular raízes quadradas diretamente. Normalmente você só precisa digitar seu número e depois pressionar o botão com o radical da segunda potência (a raiz quadrada). Por exemplo, para encontrar a raiz quadrada de 841, pressione as seguintes teclas: 8, 4, 1, (√) e acerte 29 como resposta.
Artigos sobre o tópico "Resolver raízes quadradas"
Оцените, пожалуйста статью
Popular