Calculando a área de uma elipse: 5 passos (com imagens)

Contente

Degraus
- Parte 1 de 2: Calculando a área
- Parte 2 de 2: Entenda por que funciona
Pontas

Uma elipse é uma forma bidimensional que você já deve conhecer da aula de geometria, que se parece com um círculo alongado. Calcular a área de uma elipse é fácil quando você conhece o comprimento do maior raio e do menor raio.

Degraus

Parte 1 de 2: Calculando a área

Imagem intitulada Calcular a área de uma elipse Etapa 1

1. Encontre o maior raio da elipse. Esta é a distância do centro da elipse até a borda extrema da elipse. Considere este o raio da parte `grossa` da elipse. Meça isso ou procure o rótulo apropriado no gráfico. Chamamos esse valor uma.

Você também pode chamar isso de `eixo principal principal`.

Imagem intitulada Calcular a área de uma elipse Passo 2

2. Encontre o menor raio. Como você deve ter adivinhado, o menor raio é a distância do centro ao ponto mais próximo na borda. Chamamos esse valor b.

Este raio é perpendicular ao maior raio, mas você não precisa medir ângulos para este problema.

Você também pode chamar esse raio de `eixo maior menor`.

Imagem intitulada Calcular a área de uma elipse Passo 3

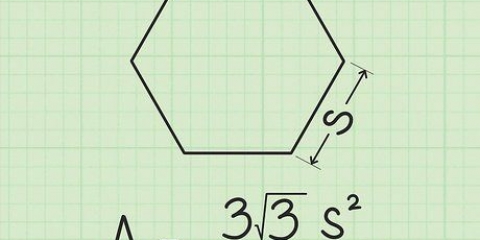
3. Multiplique por pi. A área da elipse é uma X b x. Como você está multiplicando duas unidades de comprimento, sua resposta é um quadrado.

Por exemplo, se uma elipse tem um raio maior de 5 e um raio mínimo de 3, então a área da elipse é 3 x 5 x π, ou aproximadamente 47 unidades ao quadrado.

Se você não tiver uma calculadora ou se sua calculadora não tiver um símbolo π, use `3,14` como o valor de pi.

Parte 2 de 2: Entenda por que funciona

Imagem intitulada Calcular a área de uma elipse Passo 4

1. Considere a área de um círculo. Você pode se lembrar que o área de um círculo igual a πr, que é o mesmo que π x r X r. Suponha que queremos determinar a área de um círculo como se fosse uma elipse? Medimos o raio em uma direção: r. Meça com ângulos retos: também r. Aplique isso na fórmula da área de uma elipse: π x r x r! Acontece que um círculo é apenas um tipo específico de elipse.

Imagem intitulada Calcular a área de uma elipse Passo 5

2. Imagine um círculo achatado. Imagine que um círculo é impresso na forma de uma elipse. À medida que o círculo é comprimido cada vez mais, um raio vai encurtar e o outro mais longo. A área permanece a mesma, porque nada sai do círculo. Contanto que usemos os dois raios na equação, o `aperto` e o `alongamento` se cancelarão e ainda obteremos a resposta correta.