Calculando o Apotema de um Hexágono: 15 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: Usando o teorema de Pitágoras (o comprimento do raio é fornecido)
- Método 2 de 2: Usando trigonometria (e um determinado raio)
Pontas

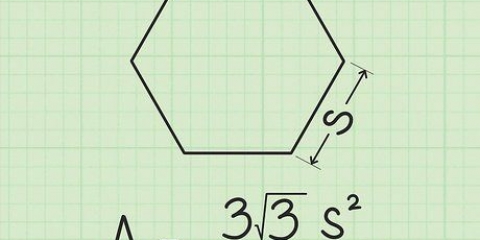
Um hexágono é um polígono com seis ângulos e lados. Quando um hexágono é regular, ele tem seis lados iguais e um apótema. Um apótema é um segmento de linha do centro de um polígono ao centro de cada lado. Normalmente o comprimento do apótema deve ser dado para calcular a área de um hexágono. Contanto que você saiba o comprimento do lado do hexágono, você pode calcular o comprimento do apótema.

Degraus

Método 1 de 2: Usando o teorema de Pitágoras (o comprimento do raio é fornecido)

Imagem intitulada Calcule o Apothem of a Hexagon Step 1

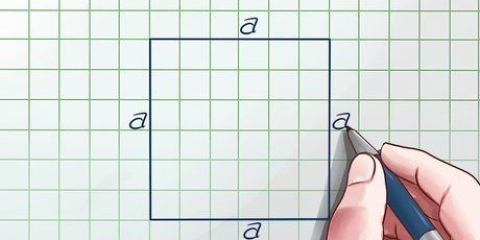
1. Divida o hexágono em seis triângulos equiláteros congruentes. Para fazer isso, desenhe uma linha de cada vértice ou ponto, até o vértice oposto.

Imagem intitulada Calcule o Apothem of a Hexagon Step 2

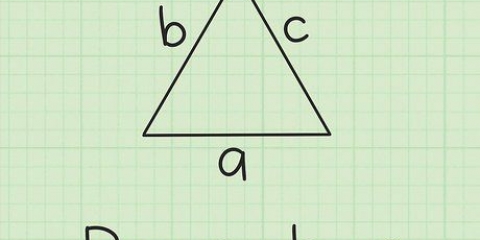
2. Escolha um triângulo e anote o comprimento da base. É igual ao comprimento do lado do hexágono.

Por exemplo, você tem um hexágono com um comprimento de 8 cm para o lado. A base de qualquer triângulo equilátero é, portanto, 8 cm.

Imagem intitulada Calcule o Apothem of a Hexagon Step 3

3. Faça dois triângulos retângulos. Você faz isso desenhando uma linha do vértice superior do triângulo equilátero perpendicular à base. Esta linha irá bissectar a base do triângulo (por isso é o apótema do hexágono). Rotule o comprimento da base de um dos triângulos retângulos.

Por exemplo, se a base do triângulo equilátero é 8 cm, então a base de qualquer triângulo retângulo -- quando você divide o triângulo em dois triângulos retângulos -- agora é igual a 4 cm.

Imagem intitulada Calcule o Apothem of a Hexagon Step 4

4. Use o teorema de Pitágoras. A fórmula é

uma 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , através do qual

c

$c$ é igual ao comprimento da hipotenusa (o lado oposto ao ângulo reto), e

uma

$uma$ e

b

$b$ ser igual aos comprimentos dos outros dois lados do triângulo.

Por exemplo, se o triângulo retângulo tem uma hipotenusa de

2

$2$ um lado de

1

$1$ e outro lado de cerca de

1, 732

$1.732$ (

\sqrt{3}

${sqrt{3}}$ ), então o teorema de Pitágoras afirma que

12 + {\sqrt{3}}^{2} = 2^{2}

$1^{{2}}+{sqrt{3}}^{{2}}=2^{{2}}$ , o que está correto quando você resolve isso:

1 + 3 = 4

$1+3=4$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 5

5. Substitua o comprimento da base do triângulo retângulo na fórmula. Substituto para

b

$b$ .

Por exemplo, se o comprimento da base for 4, sua fórmula ficaria assim:

uma 2 + 4^{2} = c^{2}

$a^{{2}}+4^{{2}}=c^{{2}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 6

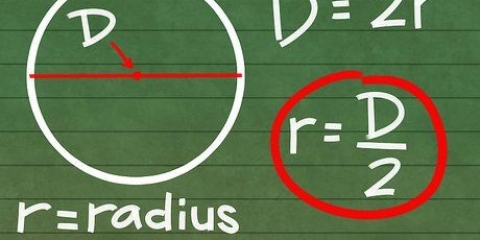
6. Substitua o comprimento da hipotenusa na fórmula. Você conhece o comprimento da hipotenusa porque conhece o comprimento do hexágono. O comprimento do lado de um hexágono regular é igual ao raio do hexágono. O raio é uma linha que liga o centro de um polígono a um de seus vértices. Você verá que a hipotenusa do triângulo retângulo também é o raio do hexágono, então o comprimento do lado do hexágono é igual ao comprimento da hipotenusa.

Por exemplo, se o comprimento do lado do hexágono é 8 cm, então o comprimento da hipotenusa do triângulo retângulo também é 8 cm. Então sua fórmula agora ficará assim:

uma 2 + 4^{2} = 8^{2}

$a^{{2}}+4^{{2}}=8^{{2}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 7

7. Quadrar os valores conhecidos da fórmula. Lembre-se que elevar ao quadrado um número é o mesmo que multiplicá-lo por ele mesmo.

Por exemplo, depois de elevar ao quadrado os valores conhecidos, sua fórmula ficará assim:

uma 2 + 16 = 64

$a^{{2}}+16=64$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 8

8. Isolar a variável desconhecida. Você faz isso subtraindo o valor ao quadrado

b

$b$ dos dois lados da equação.

Por exemplo:

uma 2 + 16 - 16 = 64 - 16

$a^{{2}}+16-16=64-16$

uma 2 = 48

$a^{{2}}=48$

Imagem intitulada Calcule o Apothem of a Hexagon Step 9

9. Resolva para uma{ estilo de exibição a} $uma$ . Você faz isso determinando a raiz quadrada de cada lado da equação. Isso lhe dará o comprimento do lado que falta do triângulo, que é igual ao comprimento do apótema do hexágono.

Por exemplo, usando uma calculadora você calcula

\sqrt{48} = 6, 93

${sqrt{48}}=6,93$ . Assim, o comprimento que falta do triângulo retângulo e, portanto, o comprimento do apótema do hexágono, é igual a 6,93 cm.

Método 2 de 2: Usando trigonometria (e um determinado raio)

Imagem intitulada Calcule o Apothem of a Hexagon Step 10

1. Escreva a fórmula para encontrar o apótema de um polígono regular. A fórmula é

apótema = s 2 bronzeado (\frac{180}{n})

${text{apothema}}={frac{s}{2tan({frac{180}{n}})}}$ , através do qual

s

$s$ é igual ao comprimento do lado do polígono e

n

$n$ é igual ao número de lados do polígono.

Imagem intitulada Calcule o Apothem of a Hexagon Step 11

2. Substituir o comprimento do lado na fórmula. Não esqueça de substituir a variável

s

$s$ .

Por exemplo, para um hexágono com um lado de 8 cm, a fórmula ficaria assim:

8 2 bronzeado (\frac{180}{n})

${frac{8}{2tan({frac{180}{n}})}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 12

3. Digite o número de lados na fórmula. Um hexágono tem 6 lados. Não esqueça de substituir a variável

n

$n$ .

Por exemplo:

8 2 bronzeado (\frac{180}{6})

${frac{8}{2tan({frac{180}{6}})}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 13

4. Arredonde o cálculo entre parênteses. Isso lhe dá o número de graus necessários para calcular a tangente.

Por exemplo,

\frac{180}{6} = 30

${frac{180}{6}}=30$ , com a qual a fórmula agora se parece com isso:

8 2 bronzeado (30)

${frac{8}{2tan(30)}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 14

5. Determine a tangente. Use uma calculadora ou tabela trigonométrica para isso.

Por exemplo, a tangente de 30 é cerca de 0,577, então a fórmula ficaria assim:

8 2 (0, 577)

${frac{8}{2(0,577)}}$ .

Imagem intitulada Calcule o Apothem of a Hexagon Step 15

6. Multiplique a tangente por 2 e depois divida o comprimento de um lado por este número. Com isso você calculou o comprimento do apótema do seu hexágono.

Por exemplo:

apótema = 8 2 (0, 577)

${text{apothema}}={frac{8}{2(0,577)}}$

apótema = 8 1, 154

${text{apothema}}={frac{8}{1.154}}$

apótema = 6, 93

${text{apothema}}=6,93$
Então o apótema de um hexágono regular com lados de 8 cm é cerca de 6,93 cm.

Pontas

O termo `apothema` pode se referir ao segmento de linha real ou ao comprimento desse segmento de linha.
Lembre-se que este método só funciona para hexágonos regulares. Hexágonos irregulares não têm apótema.