Em palavras gerais, A+B = Vamos somar os dois vetores A e B. A = <5, 9, -10> e B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, ou <22, 6, -12>. 
Em palavras gerais, A-B = Vamos subtrair os dois vetores A e B. A = <18, 5, 3> e B = <-10, 9, -10>. A - B = <18 a 10, 5 a 9, 3 a 10>, ou <28, -4, 13>. 

Observe que a ordem em que você desenha os vetores não é importante, desde que assumamos que você sempre use o mesmo ponto de partida. Vetor A + Vetor B = Vetor B + Vetor A 


Como você desenhou todos os vetores em escala e mediu os ângulos exatamente, você pode encontrar a magnitude do vetor resultante medindo o comprimento. Você também pode medir o ângulo que esta resultante faz com um vetor específico ou com a horizontal/vertical etc. para encontrar a direção. Como você não desenhou todos os vetores em escala, provavelmente terá que calcular a magnitude da resultante usando trigonometria. Use a regra do seno ou cosseno para isso. Como você está adicionando mais de dois vetores, é útil adicionar dois deles primeiro, depois adicionar sua resultante ao terceiro vetor e assim por diante. Consulte a próxima seção para obter mais informações. 
Por exemplo, se os vetores que adicionamos representam um vetor de velocidade em ms, então podemos representar o vetor resultante como "um vetor de velocidade de X ms às y em relação à horizontal". 

Por exemplo, pegamos o vetor da etapa anterior, <-2.12 e 2.12>, e adicione ao vetor <5,78 e -9>. Nesse caso, nosso vetor resultante é <-2,12+5.78 e 2.12-9>, ou <3,66 e-6,88>. 
Para encontrar a magnitude do vetor cujos componentes determinamos na etapa anterior, <3,66 e -6,88>, usamos o teorema de Pitágoras. Resolva da seguinte forma: c=(3,66)+(-6,88) c=13,40+47,33 c=√60,73 = 7,79 
Para determinar a direção do nosso vetor de exemplo, usamos θ=tan(b/a). θ=tan(-6.88/3.66) θ=tan(-1.88) θ=-61.99 
Por exemplo, se o vetor de exemplo representa uma força (em Newtons), podemos escrever isso como "um poder de 7,79 Não -61,99 da horizontal".
Calculando com vetores
Contente
Vetores são quantidades que consistem em uma magnitude e uma direção (por exemplo: vetor velocidade ou velocidade vetorial, aceleração e deslocamento), ao contrário de escalares, que possuem apenas magnitude (como velocidade, distância e energia). Enquanto escalares podem ser somados por seus tamanhos (por exemplo, 5 kJ + 6kJ = 11kJ), os vetores são um pouco mais complicados de calcular com. Consulte a Etapa 1 abaixo para saber mais sobre maneiras de fazer isso.
Degraus
Método 1 de 3: Adicionando e subtraindo vetores

1. Expresse as dimensões de um vetor usando notação vetorial. Como os vetores têm um módulo e uma direção, geralmente é fácil decompô-los em suas dimensões x, y e/ou z. Essas dimensões são geralmente expressas em uma notação equivalente a descrever um ponto em um sistema de coordenadas (por exemplo,. Observe que os vetores podem ser de 1, 2 ou 3 dimensões. Assim, os vetores podem ter um componente x, um componente x e y, ou um componente x, y etc. Nosso exemplo abaixo é sobre vetores tridimensionais, mas o processo é semelhante ao do plano ou de uma linha. Vamos supor que temos dois vetores tridimensionais, vetor A e vetor B. Podemos escrever esses vetores em notação vetorial como A =

2. Para somar dois vetores, some os componentes. Se os componentes de dois vetores são conhecidos, então é possível determinar os vetores adicionando seus componentes correspondentes. Em outras palavras, adicione o componente x do primeiro vetor ao componente x do segundo e faça o mesmo para y e z. As respostas que você obtém adicionando as componentes x, y e z dos vetores originais são as componentes x, y e z do novo vetor.

3. Para subtrair dois vetores, você subtrai seus componentes. Então o mesmo que com adição, mas ao contrário.Se os componentes de dois vetores são conhecidos, então subtrair um vetor do outro não é mais do que subtrair os componentes.
Método 2 de 3: adição e subtração usando o método da retaguarda

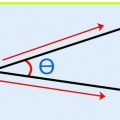
1. Indique vetores com uma seta. Como os vetores têm magnitude e direção, você pode indicá-los com uma seta. Em outras palavras, eles têm uma "ponto de partida" e um "ponto final", apontando na direção do vetor, com a magnitude do vetor indicada pela seta.
- Ao desenhar um vetor em escala, você precisa medir os ângulos com cuidado. Ângulos errados resultarão em uma resposta errada com este método.

2. Desenhe as setas na ordem traseira. A ponta da flecha é colocada contra a cauda da próxima flecha. Como você está adicionando apenas dois vetores, isso é tudo o que você precisa fazer para encontrar o vetor resultante.

3. Para subtrair faça o vetor "negativo". Subtrair vetores com este método visual é relativamente fácil. Inverta a direção do vetor, mas mantenha o mesmo tamanho e adicione-o usando o método da cabeça para a cauda como de costume. Em outras palavras, para subtrair um vetor, você gira o vetor 180 e adiciona.

4. Se você quiser adicionar ou subtrair mais de dois vetores, vincule todos esses vetores um após o outro usando o método traseiro. A ordem não importa. Você pode usar isso para qualquer número de vetores.
5. Desenhe um novo vetor da cauda do primeiro vetor até a cabeça do último. Esteja você trabalhando com 2 ou 100 vetores, o vetor que se estende do ponto inicial (a cauda do seu primeiro vetor) até o ponto final dos vetores adicionados (a cabeça do seu último vetor) é o resultado vetor, ou a soma de todos os vetores. Observe que este vetor é igual ao vetor obtido pela soma das componentes x, y e/ou z de todos os vetores.


6. Exiba o vetor resultante por tamanho e direção. Os vetores são determinados pelo seu comprimento e direção. Como dito acima, supondo que você tenha desenhado os vetores com precisão, a magnitude do vetor é igual ao seu comprimento e direção, e seu ângulo é relativo à vertical, horizontal, etc. Use as unidades dos vetores que você somou para escolher as unidades para a magnitude do vetor resultante.
Método 3 de 3: Adicionando e subtraindo vetores determinando os componentes

1. Use trigonometria para encontrar os componentes do vetor. Você precisa da magnitude e direção em relação à horizontal ou vertical e precisa ter algum conhecimento prático de trigonometria. Suponha que temos um vetor 2-D. Primeiro você faz os vetores a hipotenusa de um triângulo retângulo, com os outros dois lados paralelos aos eixos x e y. Você pode pensar nesses dois lados como vetores cabeça-cauda que, quando somados, produzem o vetor original.
- Os comprimentos dos dois lados são iguais às magnitudes dos componentes xey do seu vetor e podem ser calculados usando trigonometria. Se x é a magnitude do vetor, então o lado adjacente ao ângulo do vetor (em relação à horizontal, vertical, etc.) igual a xcos(θ), enquanto o contrário é igual a xsen(θ).
- Também é importante considerar a orientação de seus componentes. Se o componente aponta na direção negativa de um dos eixos, recebe um sinal de menos. Por exemplo, se um componente aponta para a esquerda ou para baixo no plano, ele recebe um sinal de menos.
- Por exemplo, digamos que temos um vetor de magnitude 3 e uma direção 135 em relação à horizontal. Com esta informação podemos determinar que a componente x é igual a 3cos(135) = -2.12 e o componente y é 3sin(135) = 2.12

2. Some os componentes correspondentes de dois ou mais vetores. Quando você encontrar os componentes de todos os vetores, basta somar as magnitudes para encontrar os componentes do seu vetor resultante. Primeiro some os tamanhos dos componentes horizontais (paralelos ao eixo x). Em seguida, adicione os tamanhos dos componentes verticais (paralelos ao eixo y). Se um componente tiver um sinal de menos (-) na frente dele, seu tamanho será subtraído. As respostas que você obtém são os componentes do seu vetor resultante.

3. Calcule a magnitude do vetor resultante usando o teorema de Pitágoras. Com esta declaração, c=a+b, você pode encontrar o comprimento dos lados de triângulos retângulos?. Como o triângulo formado pelo vetor resultante e seus componentes é um triângulo retângulo, podemos usar este teorema para encontrar o comprimento do vetor e, portanto, sua magnitude. De c como a magnitude do vetor resultante que você está tentando encontrar, digamos uma em como o tamanho do componente x e b como a magnitude do componente y. Resolva com álgebra.

4. Calcule a direção da resultante com a tangente. Finalmente, determinamos a direção do vetor resultante. Use a fórmula θ=tan(b/a), onde θ é o ângulo que a resultante faz com o eixo x a partir da horizontal, onde b é a magnitude da componente y e a é a magnitude da componente x.

5. Exiba o vetor resultante por tamanho e direção. Como indicado acima, os vetores são definidos por sua magnitude e direção. Certifique-se de usar as unidades corretas para o tamanho do vetor.
Pontas
- Vetores não devem ser confundidos com tamanhos.
- Você pode encontrar o tamanho de um vetor no espaço pela fórmula a=b+c+d usar, onde uma é a magnitude do vetor e b, c e d os componentes em cada direção.
- Vetores representados como xeu + yj + zk pode ser adicionado ou subtraído simplesmente adicionando ou subtraindo os coeficientes dos três vetores. A resposta é então também na forma i, j, k.
- Os vetores de coluna podem ser adicionados e subtraídos, adicionando ou subtraindo os valores em cada linha.
Artigos sobre o tópico "Calculando com vetores"
Оцените, пожалуйста статью
Popular