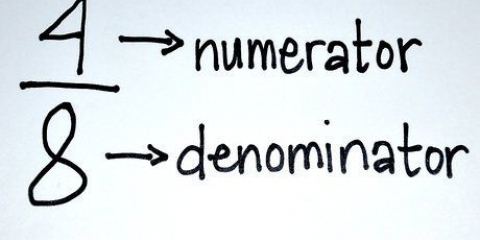
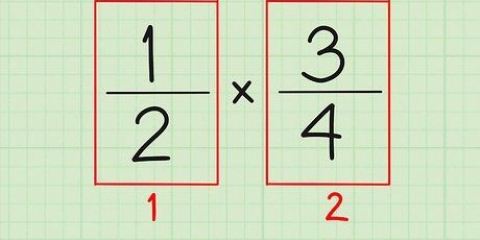
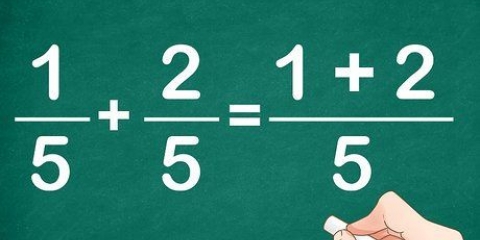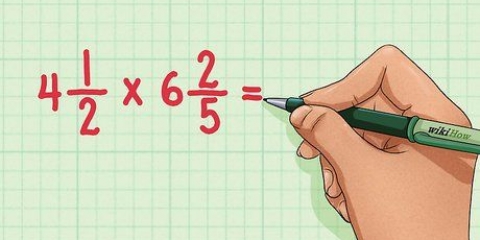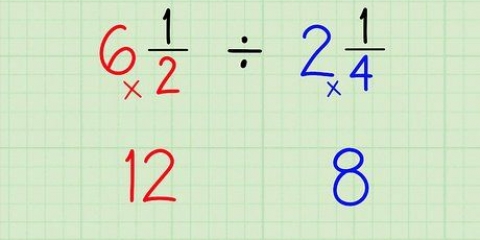Então, se você tentar resolver 2/x = 10/13 para x, obterá 2 * 13 = x * 10, ou 26 = 10x. 



Então, combine 4x e 2x por meio de 2x subtrair de ambos os lados da equação. Trabalhado, isso produz a seguinte equação 2x + 12 = 2. Combinar agora 12 e 2 por meio de 12 subtrair de ambos os lados da equação. Deu certo ficou assim: 2x + 12-12 = 2-12. Então a equação fica: 2x = -10. 
Multiplicação cruzada
Contente
A multiplicação cruzada é uma maneira de resolver uma equação, com uma variável como parte de duas frações iguais entre si. A variável é um número ou quantidade desconhecida, e a multiplicação cruzada torna essa equação fracionária uma equação simples, permitindo que você resolva a variável em questão. A multiplicação cruzada é especialmente útil ao tentar resolver uma razão. Aqui está como fazer isso.
Degraus
Método 1 de 2: Multiplicação cruzada por uma variável

1. Multiplique o numerador da fração da esquerda pelo denominador da fração da direita. Digamos que você esteja trabalhando na equação 2/x = 10/13. Agora multiplique 2 por 13. 2 x 13 = 26.

2. Multiplique o numerador da fração da direita pelo denominador da fração da esquerda. Multiplicar por 10. x * 10 = 10x. Você pode fazer a multiplicação cruzada nesta direção primeiro; não importa no final, desde que você multiplique ambos os numeradores pelos denominadores diagonais da outra fração.

3. Faça os dois produtos iguais entre si. Faça 26 igual a 10x. 26 = 10x. Não importa qual número você pegue primeiro; por serem equivalentes, você pode movê-los de um lado da equação para o outro sem consequências; se você tratar cada termo como um todo.

4. Resolva para a variável. Agora que você está lidando com 26 = 10x, você pode começar a encontrar o denominador comum dividindo 26 e 10 por um número pelo qual ambos os denominadores são divisíveis. Como ambos são números pares, é possível dividi-los por 2; 26/2 = 13 e 10/2 = 5. Agora você fica com 13 = 5x como uma equação. Então, para isolar x, divida ambos os lados da equação por 5. Então 13/5 = 5/5, ou 13/5 = x. Se você quiser a resposta como uma fração decimal ou decimal, você pode dividir ambos os lados da equação por 10 para obter 26/10 = 10/10, ou 2.6 = x.
Método 2 de 2: Multiplicação Cruzada com Várias Variáveis

1. Multiplique o numerador da fração da esquerda pelo denominador da fração da direita. Digamos que você esteja trabalhando na seguinte equação: (x + 3)/2 = (x + 1)/4. Multiplicar (x + 3) de 4 para 4(x +3) para obter. Isso está sendo trabalhado 4x + 12.

2. Multiplique o numerador da fração da direita pelo denominador da fração da esquerda. Repita este procedimento do outro lado. (x+1) x 2 = 2(x +1). Torna-se 2(x +1) então 2x + 2.

3. Faça os dois produtos iguais entre si e combine termos iguais. Agora você tem 4x + 12 = 2x + 2. Combine o X termos e as constantes em ambos os lados da equação.

4. Resolver. Tudo o que você precisa fazer agora é dividir ambos os lados da equação por 2. 2x/2 = -10/2 = x = -5. Após a multiplicação cruzada, você verá que x = -5. Você pode voltar e verificar se tudo está correto digitando -5 para x para garantir que ambos os lados da equação sejam iguais. O resultado desta verificação é -1 = -1, e isso é verdade porque ambos os lados da equação são iguais. O controle, por exemplo,. 0 = -1 retornar a equação não está correta, então algo deu errado.
Pontas
- Observe que, se você inserir outro número (por exemplo, 5) na mesma equação, obterá o seguinte resultado: 2/5 = 10/13. Mesmo se você multiplicar o lado esquerdo da equação por 5/5 novamente, você obtém 10/25 = 10/13, o que está claramente errado. Este último caso mostra claramente que você cometeu um erro ao multiplicar transversalmente.
Artigos sobre o tópico "Multiplicação cruzada"
Оцените, пожалуйста статью
Popular