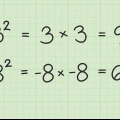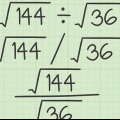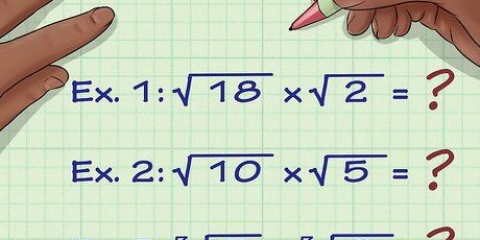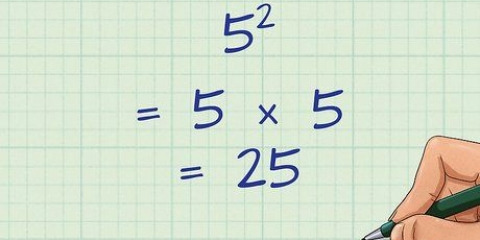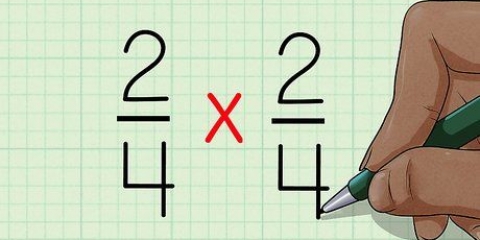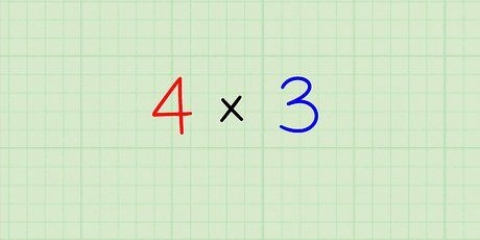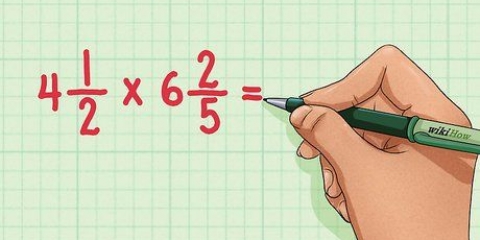Multiplicando Raízes Quadradas: 8 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: Multiplicando raízes quadradas sem coeficientes
- Método 2 de 2: Multiplicando raízes quadradas com coeficientes
Pontas
Necessidades

Assim como multiplicar inteiros, você também pode multiplicar raízes quadradas (uma equação de raiz quadrada) juntos. Às vezes, raízes quadradas têm coeficientes (um número inteiro antes do radical), mas isso apenas adiciona um passo à multiplicação e não altera o processo. A parte mais complicada da multiplicação de raiz quadrada é simplificar a expressão para obter a resposta final, mas mesmo essa etapa é fácil se você souber seus quadrados perfeitos.

Degraus

Método 1 de 2: Multiplicando raízes quadradas sem coeficientes

Imagem intitulada Multiplicar Raízes Quadradas Passo 1

1. Multiplique as raízes. Um radicando (inglês) é um número abaixo do radical. Multiplique raízes da mesma forma que números inteiros. Certifique-se de que o produto permaneça abaixo do sinal de radical.

Por exemplo, se você calcular $\sqrt{15} \times \sqrt{5}$ ${sqrt{15}}times {sqrt{5}}$ , então você consegue $15 \times 5 = 75$ $15vezes 5=75$ . assim, $\sqrt{15} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}times {sqrt{5}}={sqrt{75}}$ .

Imagem intitulada Multiplicar Raízes Quadradas Passo 2

2. Derive quaisquer quadrados perfeitos da raiz quadrada. Você faz isso verificando se um quadrado perfeito é um fator do número sob o radical. Se você não conseguir derivar um quadrado perfeito, sua resposta já foi simplificada e você não precisa fazer mais nada.

Um quadrado perfeito é o resultado da multiplicação de um número (inteiro positivo ou negativo) por ele mesmo. Por exemplo: 25 é um quadrado perfeito porque

5 \times 5 = 25

$5vezes 5=25$ .

Por exemplo,

\sqrt{75}

${sqrt{75}}$ pode ser fatorado no quadrado perfeito 25:

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25vezes 3}}$

Imagem intitulada Multiplicar Raízes Quadradas Passo 3

3. Coloque a raiz quadrada antes do radical. Deixe o outro fator sob o radical. Agora você tem a expressão simplificada.

Por exemplo,

\sqrt{75}

${sqrt{75}}$ pode ser dissolvido em

\sqrt{25 \times 3}

${sqrt{25vezes 3}}$ , para a raiz quadrada de 25 (que é 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25vezes 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

Imagem intitulada Multiplicar raízes quadradas Passo 4

4. Calcular o quadrado de uma raiz quadrada. Em alguns casos, você precisa multiplicar uma raiz quadrada por ela mesma. Elevar um número ao quadrado e tirar a raiz quadrada de um número são operações opostas; então eles se desfazem. O resultado do quadrado de uma raiz quadrada é simplesmente o número sob o radical.

Por exemplo,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}}times {sqrt{25}}=25$ . Você obtém este resultado porque

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}}times {sqrt{25}}=5times 5=25$ .

Método 2 de 2: Multiplicando raízes quadradas com coeficientes

Imagem intitulada Multiplicar Raízes Quadradas Passo 5

1. Multiplique os coeficientes. Um coeficiente é um número para o radical. Apenas ignore o radical e o número abaixo dele e multiplique os dois inteiros juntos. Coloque seu produto antes do primeiro radical.

Cuidado com os sinais de mais e menos ao multiplicar coeficientes. Lembre-se que um número negativo vezes um número positivo produz um resultado negativo, e um número negativo vezes um número negativo produz um resultado positivo.
Por exemplo, ao calcular $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}}times 2{sqrt{6}}$ , calcule primeiro $3 \times 2 = 6$ $3vezes 2=6$ . Agora a tarefa é a seguinte: $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}times {sqrt{6}}$ .

Imagem intitulada Multiplicar Raízes Quadradas Passo 6

2. Multiplique os números sob os radicais. Para fazer isso, multiplique os números como se fossem inteiros. Certifique-se de que o produto permaneça sob o sinal radical.

Por exemplo, para uma declaração como

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}times {sqrt{6}}$ , calcule o produto dos números sob os radicais usando

2 \times 6 = 12

$2vezes 6=12$ , de modo a

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}}times {sqrt{6}}={sqrt{12}}$ . A tarefa agora se parece com isso:

6 \sqrt{12}

$6{sqrt{12}}$ .

Imagem intitulada Multiplicar Raízes Quadradas Passo 7

3. Se possível, fatore quaisquer quadrados sob o sinal de radical. Você precisa fazer isso para simplificar sua resposta. Se você não conseguir resolver um quadrado, sua resposta já foi simplificada e você pode pular esta etapa.

Um quadrado é o resultado da multiplicação de um inteiro (positivo ou negativo) por ele mesmo. Por exemplo: 4 é um quadrado, porque

2 \times 2 = 4

$2vezes 2=4$ .

Por exemplo:

\sqrt{12}

${sqrt{12}}$ pode ser fatorado de modo que o quadrado de 4 seja colocado antes do radical:

\sqrt{12}

${sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4vezes 3}}$

Imagem intitulada Multiplicar Raízes Quadradas Passo 8

4. Multiplique a raiz do quadrado pelo coeficiente. Deixe o outro fator sob o radical. Isso produz uma expressão simplificada.

Por exemplo,

6 \sqrt{12}

$6{sqrt{12}}$ pode ser dissolvido em

6 \sqrt{4 \times 3}

$6{sqrt{4vezes 3}}$ , depois disso você pode tirar a raiz quadrada de 4 (ou seja, 2) e depois multiplicar isso por 6:

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4vezes 3}}$
=

6 \times 2 \sqrt{3}

$6vezes 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Pontas

Conheça seus quadrados, pois isso facilita muito esse processo!
Siga as regras usuais para o sinal de um número para determinar se o novo coeficiente será positivo ou negativo. Um coeficiente positivo multiplicado por um coeficiente negativo produz um número negativo. Dois coeficientes positivos multiplicados ou dois coeficientes negativos multiplicados juntos resultam em um número positivo.
Todos os termos sob o radical são sempre positivos, então você não precisa se preocupar com o sinal ao multiplicar números sob um radical.