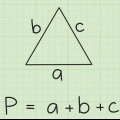Qualquer lado do triângulo pode ser a base, não importa como o triângulo é desenhado. Para imaginar isso, gire o triângulo em sua mente até que o lado muito familiar se torne o fundo. Por exemplo, se você sabe que a área de um triângulo é 20 e um de seus lados é 4, então: A = 20 e b = 4. 
No exemplo: 20 = 1/2(4)h 20 = 2h 10 = h 

Assim no exemplo:c = 8 e a = 4. 
4 + b = 8 16 + b = 64 b = 48 
b = Quadrado (48) = 6,93
Calculando a altura de um triângulo
Contente
Para calcular a área de um triângulo você precisa de sua altura. Se esta informação não for fornecida, você pode facilmente calculá-la com base no que você sabe! Este artigo ensinará duas maneiras diferentes de encontrar a altura de um triângulo, dependendo de quais informações você recebeu.
Degraus
Método 1 de 2: Determinando a altura quando a área e a base são conhecidas

1. A fórmula da área de um triângulo. Isto éA = 1/2 bh.
- uma = área do triângulo
- b = Comprimento da base do triângulo
- h = Altura da base do triângulo

2. Olhe para o triângulo e determine quais variáveis são conhecidas. Neste caso você já conhece a área, então uma é igual a esse valor.Você também deve saber o valor de um dos lados; indique esse valor "`b`".Se você não conhece os dois valores ou um deles, precisa de outro método.

3. Use seus valores na equaçãoA = 1/2 bh e calcular. Primeiro multiplique a base (b) por 1/2, depois divida a área (A) pelo produto.O valor resultante é a altura do seu triângulo!
Método 2 de 2: Encontrando a Altura de um Triângulo Equilátero

1. Propriedades de um triângulo equilátero. Um triângulo equilátero tem três lados iguais e três ângulos iguais de 60 graus cada. Se você dividir um triângulo equilátero ao meio, você terminará com dois triângulos retângulos congruentes.
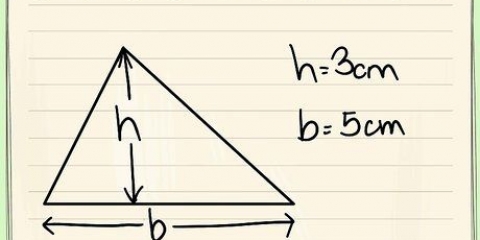
- Neste exemplo, usaremos um triângulo equilátero com lados que têm um comprimento de 8.
2. O teorema de Pitágoras. O teorema de Pitágoras afirma que para um triângulo retângulo com lados de comprimento uma e b, e uma hipotenusa de comprimento c: a + b = c.Podemos usar este teorema para encontrar a altura do nosso triângulo equilátero!

3. Divida o triângulo equilátero ao meio e atribua valores às variáveisuma, b ec.Lateral uma é igual a metade do comprimento de um lado, e lado b é a altura do triângulo que queremos resolver.

4. Preencha os valores no teorema de Pitágoras e resolva para b. Primeiro calcule o quadrado de c e uma multiplicando-o por ele mesmo. Então subtraia a de c.

5. Encontre a raiz quadrada de b para encontrar a altura do triângulo! Use a raiz quadrada em sua calculadora para encontrar Sqrt(. A resposta é a altura do seu triângulo equilátero!
Artigos sobre o tópico "Calculando a altura de um triângulo"
Оцените, пожалуйста статью
Popular