Para desenhar o polígono, use uma régua e desenhe cada lado com o mesmo comprimento, conectando todos os lados. Se você não tiver certeza da aparência do polígono, pesquise imagens online. Por exemplo, um sinal de pare é um octógono. 
Para um quadrado, desenhe uma linha do canto inferior esquerdo ao canto superior direito e outra linha do canto inferior direito ao canto superior esquerdo. Desenhe diagonais em cores diferentes para facilitar a contagem. Observe que este método se torna muito mais difícil com polígonos com mais de dez lados. 
Para o quadrado existem duas diagonais: uma diagonal para cada dois vértices. Um hexágono tem nove diagonais: há três diagonais para cada três vértices. Um heptágono tem 14 diagonais. Além do heptágono torna-se mais difícil contar as diagonais porque existem muitas diagonais. 
Por exemplo, um pentágono (cinco lados) tem apenas cinco diagonais. Cada vértice tem duas diagonais, então se você contar cada diagonal de cada vértice duas vezes, você pensaria que existem 10 diagonais. Isso está incorreto porque você contou cada diagonal duas vezes! 
Um hexágono ou hexágono tem 9 diagonais. Um heptágono tem 14 diagonais. 

Tetra (4), penta (5), hexa (6), hepta (7), octa (8), enea (9), deca (10), hendeca (11), dodeca (12), trideca (13), tetradeca (14), pentadeca (15), etc. Para polígonos muito grandes com muitos lados, você pode ver apenas `n-goon` onde `n` é o número de lados. Por exemplo, um polígono de 44 lados é escrito como 44-goon. Quando você obtém uma imagem do polígono, pode simplesmente contar o número de lados. 
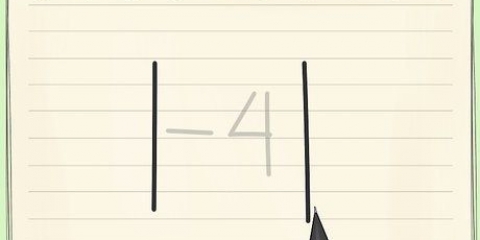
Exemplo: Um dodecágono tem 12 lados. Escreva a equação: n(n-3)/2 Processe isso na variável: (12(12 - 3))/2 
Por exemplo: (12(12 - 3))/2 Subtrair: (12*9)/2 Multiplicar: (108)/2 Compartilhar: 54 Então um dodecágono tem 54 diagonais. 
Hexágono (6 lados): n(n-3)/2=6(6-3)/2=6*3/2=18/2=9 diagonais. Decágono (10 lados): n(n-3)/2=10(10-3)/2=10*7/2=70/2=35 diagonais. Icoságono (20 lados): n(n-3)/2=20(20-3)/2=20*17/2=340/2=170 diagonais. 96 tontos (96 lados): 96(96-3)/2=96*93/2=8928/2=4464 diagonais.
Determine o número de diagonais em um polígono
Contente
Encontrar diagonais em um polígono é uma habilidade necessária para progredir em matemática. Pode parecer difícil no começo, mas é bem fácil quando você aprende a fórmula básica. Uma diagonal é qualquer segmento desenhado entre os vértices de um polígono que não contém os lados desse polígono. Um polígono é qualquer forma que tenha mais de três lados. Usando uma fórmula muito simples, você pode calcular o número de diagonais em qualquer polígono, seja ele de quatro lados ou 4000 lados.
Degraus
Método 1 de 2: Desenhando as diagonais

1. Conheça os nomes dos diferentes polígonos. Você pode primeiro precisar determinar quantos lados o polígono tem. Todo polígono tem um prefixo que indica o número de lados. Aqui estão os nomes dos polígonos de até vinte lados:
- Quadrilátero/Tetragone: 4 lados
- Pentágono/pentágono: 5 lados
- Hexágono/Hexágono: 6 lados
- Heptágono: 7 lados
- Octógono/Ocagon: 8 lados
- Nonagoon/Eneagon: 9 lados
- Decágono: 10 lados
- Hendecágono: 11 lados
- Dodecágono: 12 lados
- Triskaidecagon: 13 lados
- Tetradecágono: 14 lados
- Pentadecágono: 15 lados
- Hexadecágono: 16 lados
- Heptadecágono: 17 lados
- Octadecágono: 18 lados
- Enneadecágono: 19 lados
- Iconsagon: 20 lados
- Observe que um triângulo não tem diagonais.

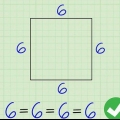
2. Desenhe o polígono. Se você quer saber quantas diagonais existem em um quadrado, comece desenhando o quadrado. A maneira mais fácil de encontrar e contar as diagonais é desenhar o polígono simetricamente, onde cada lado tem o mesmo comprimento. É importante notar que mesmo que o polígono não seja simétrico, ele ainda tem o mesmo número de diagonais.

3. Desenhe as diagonais. Uma diagonal é um segmento desenhado de um canto a outro da forma, excluindo os lados do polígono. Use uma régua para desenhar uma diagonal para qualquer outro vértice disponível.

4. Conte as diagonais. Existem duas opções para contar as diagonais: você pode contá-las quando desenha as diagonais ou quando são desenhadas. Ao contar cada diagonal, escreva um pequeno número acima da diagonal para indicar que foi contada. É fácil se perder enquanto conta quando muitas diagonais se entrelaçam.

5. Tenha cuidado para não contar suas diagonais mais de uma vez. Cada vértice pode ter várias diagonais, mas isso não significa que o número de diagonais é igual ao número de vértices vezes o número de diagonais. Ao contar as diagonais, certifique-se de contar cada diagonal apenas uma vez.

6. Pratique com alguns exemplos. Desenhe alguns outros polígonos e conte o número de diagonais. O polígono não precisa ser simétrico para que este método funcione. No caso de um polígono côncavo você pode precisar desenhar algumas diagonais fora do polígono real.
Método 2 de 2: Usando a fórmula para a diagonal

1. Defina a fórmula. A fórmula para encontrar o número de diagonais de um polígono é n(n-3)/2 onde `n` é igual ao número de lados do polígono. Usando a propriedade distributiva, isso pode ser reescrito como (n - 3n)/2. Você pode olhar para os dois lados, ambas as equações são idênticas.
- Esta equação pode ser usada para encontrar o número de diagonais de qualquer polígono.
- Observe que o triângulo é uma exceção a esta regra. Devido à forma do triângulo, não tem diagonais.

2. Determine o número de lados do polígono. Para usar esta fórmula você precisa saber o número de lados do polígono. O número de lados é dado no nome do polígono, então você só precisa saber o que cada nome significa. Aqui estão alguns prefixos comuns que você pode encontrar com polígonos:

3. Incorporar o número de lados na equação. Depois de saber quantos lados o polígono tem, você só precisa fatorar esse número na equação e resolver a equação. Onde quer que você veja `n` na equação, o número de lados do polígono é substituído pelo número de lados do polígono.

4. Resolva a equação. Finalmente, resolva a equação na ordem correta das operações. Comece resolvendo a subtração, depois a multiplicação e finalmente a divisão. A última resposta é o número de diagonais que o polígono tem.

5. Pratique com mais exemplos. Quanto mais prática você tiver com um conceito matemático, melhor poderá usá-lo. Elaborar muitas questões práticas também o ajudará a lembrar da fórmula caso precise dela para um teste, teste ou exame. Lembre-se que esta fórmula funciona para um polígono com qualquer número de lados maior que três.
Artigos sobre o tópico "Determine o número de diagonais em um polígono"
Оцените, пожалуйста статью
Similar
Popular