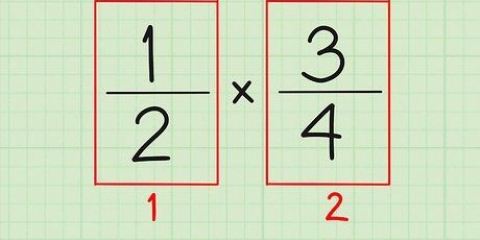
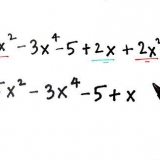Em nosso exemplo, o denominador da fração empilhada (11/15)/(29/70) é a fração 29/70. Para encontrar o inverso, invertemos e a fração se torna 70/29. Observe que, se a fração empilhada tiver um número inteiro no denominador, você poderá tratá-la como uma fração e ainda encontrar seu inverso. Por exemplo, suponha que a fração empilhada fosse (11/15)/(29), então podemos definir o denominador como 29/1, com o recíproco 29/01. 
Em nosso exemplo, multiplicamos 11/15 × 70/29. 70 × 11 = 770 e 15 × 29 = 435. Assim é a nossa nova fração simples 770/435. 
Um divisor comum de 770 e 435 é 5. Então, se dividirmos o numerador e o denominador da nossa fração por 5, obtemos 154/87. 154 e 87 não têm fatores comuns, então sabemos que encontramos a resposta final! 

Isso é mais fácil de entender com um exemplo. Vamos tentar simplificar a fração empilhada que mencionamos acima, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). Os termos de fração nesta fração composta são (1)/(x+3) e (1)/(x-5). O denominador comum dessas duas frações é o produto de seus denominadores: (x+3)(x-5). 
Em nosso exemplo, multiplicamos a fração empilhada (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), por ((x+ 3 )(x-5))/((x+3)(x-5)). Precisaremos multiplicar pelo numerador e denominador da fração empilhada, multiplicando cada termo por (x+3)(x-5). Primeiro vamos multiplicar o numerador: (((1)/(x+3)) + x - 10) × (x+3)(x-5) = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5)) = (x-5) + (x(x - 2x - 15)) - (10(x - 2x - 15)) = (x-5) + (x - 2x - 15x) - (10x - 20x - 150) = (x-5) + x - 12x + 5x + 150 = x - 12x + 6x + 145 
O denominador da nossa fração empilhada, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), é x +4 +(( 1)/(x-5)). Vamos multiplicar isso pelo kgd que encontramos, (x+3)(x-5). (x +4 +((1)/(x - 5))) × (x+3)(x-5) = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5). = x(x - 2x - 15) + 4(x - 2x - 15) + ((x+3)(x-5))/(x-5) = x - 2x - 15x + 4x - 8x - 60 + (x+3) = x + 2x - 23x - 60 + (x+3) = x + 2x - 22x - 57 
Usando o numerador e o denominador que encontramos acima, podemos construir uma fração que é igual à nossa fração empilhada inicial, mas não contém frações. O numerador que obtivemos foi x - 12x + 6x + 145 e o denominador foi x + 2x - 22x - 57, então a nova fração é: (x - 12x + 6x + 145)/(x + 2x - 22x - 57)
Simplifique as frações empilhadas
Contente
Frações empilhadas são aquelas em que o numerador, denominador ou ambos contêm frações. Por esse motivo, você também pode chamar isso de `frações em frações`. Simplificar frações empilhadas é um processo que pode variar de fácil a difícil com base em quantos termos estão presentes no numerador e denominador, se algum dos termos é variável e, em caso afirmativo, a complexidade dos termos variáveis. Veja o passo 1 abaixo para começar!
Degraus
Método 1 de 2: Simplificando frações empilhadas com multiplicação reversa

1. Se necessário, simplifique o numerador e o denominador para algumas frações. Frações empilhadas não são necessariamente difíceis de resolver. Na verdade, frações empilhadas em que o numerador e o denominador contêm uma única fração são geralmente muito fáceis de resolver. Portanto, se o numerador ou denominador de sua fração empilhada (ou ambos) contiver várias frações ou frações e números inteiros, simplifique conforme desejado para obter uma única fração no numerador e no denominador. Isso pode exigir o Mínimo Múltiplo Comum (MMC) encontrar duas ou mais frações.
- Suponha que queremos simplificar a fração complexa (3/5 + 2/15)/(5/7 - 3/10). Primeiro, podemos simplificar o numerador e o denominador de nossa fração complexa para frações simples.
- Para simplificar o numerador, vamos pegar um LCF de 15, multiplicando 3/5 por 3/3. Nosso contador se torna 15/09 + 15/02, o que equivale a 15/11.
- Para simplificar o denominador, vamos pegar um lcm de 70, multiplicando 5/7 por 10/10 e 3/10 por 7/7. Nosso denominador será 50/70 - 21/70, que é igual a 29/70.
- Então nossa nova fração empilhada é (15/11)/(29/70).

2. Inverta o denominador e encontre o inverso. Por definição, partes de um número para outro o mesmo que o multiplicando o primeiro número pelo inverso do segundo número. Agora que obtivemos uma fração empilhada com uma única fração no numerador e no denominador, podemos usar essa propriedade de divisão para simplificar nossa fração empilhada! Primeiro encontre o inverso do denominador da fração empilhada. Faça isso `invertendo` a fração - o numerador substitui o denominador e vice-versa.

3. Multiplique o numerador da fração empilhada pelo inverso do denominador. Agora que você obteve o inverso do denominador da sua fração empilhada, multiplique-o pelo numerador para obter uma única fração simples! Lembre-se, para multiplicar duas frações, não multiplicamos transversalmente - o numerador da nova fração é o produto do numerador das duas antigas, e o denominador também.

4. Simplifique a nova fração encontrando o máximo divisor comum. Agora temos uma única fração simples, então tudo o que resta é representá-la nos termos mais simples possíveis. Especial máximo divisor comum (mdc) do numerador e denominador e dividir ambos por este número para simplificar.
Método 2 de 2: simplificando frações empilhadas com termos variáveis

1. Sempre que possível, use o método de multiplicação inversa conforme descrito acima. Para ser claro, praticamente qualquer fração empilhada pode ser simplificada reduzindo o numerador e o denominador a frações simples e multiplicando o numerador pelo inverso do denominador. Frações empilhadas de variáveis não são exceção, mas quanto mais complicadas forem as expressões de variáveis na fração empilhada, mais difícil e demorado será realizar a multiplicação reversa. Para frações empilhadas `simples` com variáveis, a multiplicação pelo inverso é uma boa escolha, mas frações empilhadas com vários termos variáveis no numerador e denominador podem ser mais fáceis de simplificar usando o método alternativo descrito abaixo.
- Por exemplo: (1/x)/(x/6) é fácil de simplificar com a multiplicação inversa. 1/x × 6/x = `6/x. Não é necessário usar um método alternativo.
- No entanto, a fração (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) é mais difícil de simplificar com a multiplicação reversa. Reduzir o numerador e o denominador dessa fração empilhada a frações simples, multiplicar inversamente e reduzir o resultado aos termos mais simples, é provavelmente um processo complicado. Neste caso, o método alternativo abaixo pode ser mais fácil.

2. Se a multiplicação inversa for impraticável, comece encontrando o menor divisor comum dos termos da divisão na fração empilhada. O primeiro passo neste método alternativo de simplificação é encontrar o kgd de todos os termos fracionários na fração empilhada - tanto no numerador quanto no denominador. Se um ou mais termos fracionários têm variáveis em seus denominadores, o kgd é simplesmente o produto de seus denominadores.

3. Multiplique o numerador da fração empilhada pelo kgd. Em seguida, precisamos multiplicar os termos em nossa fração empilhada pelo kgd de seus termos fracionários. Em outras palavras, multiplicaremos toda a fração empilhada por (kgd)/(kgd). Podemos fazer isso simplesmente porque (kgd)/(kgd) é igual a 1. Primeiro multiplique o numerador por ele mesmo.

4. Multiplique o denominador da fração empilhada pelo kgd como você fez com o numerador. Multiplique a fração empilhada pelo kgd que você encontrou indo para o denominador. Multiplique cada termo pelo kgd.

5. Forme uma nova fração simplificada a partir do numerador e denominador que você acabou de encontrar. Depois de multiplicar sua fração por sua expressão (kgd)/(kgd) e simplificá-la riscando termos semelhantes, você deve ficar com uma fração simples que não contém termos fracionários. Como você deve ter notado, os denominadores dessas frações se cancelam (multiplicando as frações na fração empilhada original pelo kgd), deixando termos variáveis e inteiros no numerador e denominador de sua resposta, mas não frações.
Pontas
- Mostre cada passo do seu trabalho. As frações podem ser confusas se você quiser ir rápido demais ou tentar tirá-las da cabeça.
- Procure exemplos de frações empilhadas online ou em seu livro didático. Siga cada passo até dominá-lo.
Artigos sobre o tópico "Simplifique as frações empilhadas"
Оцените, пожалуйста статью
Popular