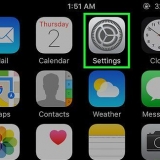
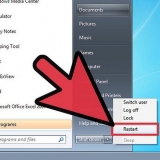
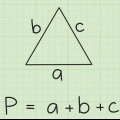a + b > c = 17 > 5 a + c > b = 12 > 10 b + c > uma = 15 > 7 
5 + 8 > 3 = 13 > 3, então este lado está correto. 5 + 3 > 8 = 8 > 8. Porque isso não está certo, você pode parar agora. Isso não é um triângulo.
Determine se três comprimentos juntos formam um triângulo
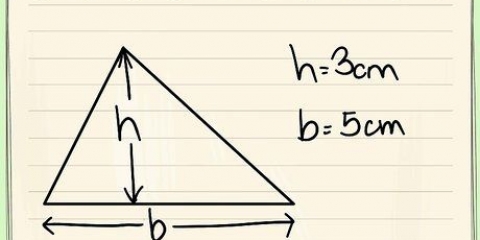
Determinar se os comprimentos de três lados juntos formam um triângulo é mais fácil do que parece. Tudo o que você precisa fazer é usar o Teorema da Desigualdade do Triângulo, que afirma que a soma dos comprimentos de dois lados de um triângulo é sempre maior que o terceiro lado. Se isso se aplica a todas as três combinações dos comprimentos adicionados, você está lidando com um triângulo.
Degraus

1. Aprenda o Teorema da Desigualdade do Triângulo. Este teorema afirma que a soma de dois lados de um triângulo deve ser maior que o terceiro lado. Se isso se aplica a todas as três combinações, você tem um triângulo verdadeiro. Você terá que verificar essas combinações, uma a uma, para ter certeza de que um triângulo pode ser formado. Você também pode considerar o triângulo como os lados dos comprimentos a, b e c, e o teorema como desigualdade: a+b > c, a+c > b e b+c > uma.
- Um exemplo, uma = 7, b = 10 e c = 5.

2. Verifique se a soma dos dois primeiros lados é maior que o terceiro. Neste caso, você pode usar os lados uma e b somar, ou seja, 7 + 10, para obter 17, que é maior que 5. Você também pode pensar nisso como 17 > 5.

3. Verifique se a soma da próxima combinação de dois lados é maior que o lado restante. Bem, veja se a soma dos lados uma e c é maior que o lado b. Isso significa que você tem que ver se 7 + 5, ou 12, é maior que 10. 12 > 10, então está certo.

4. Verifique se a soma da última combinação de dois lados é maior que o lado restante. Você terá que verificar se a soma dos lados b e seda c é maior que a seda uma. Para fazer isso, você terá que verificar se 10 + 5 é maior que 7. 10 + 5 = 15 e 15 > 7, então o triângulo está correto para todos os lados.

5. Verifique seu trabalho. Agora que você verificou todos os lados um por um, você pode verificar novamente se a regra se aplica a todas as três combinações. Se a soma de um dos dois lados for maior que o terceiro em qualquer combinação, como neste triângulo, você determinou que o triângulo é válido. Se a regra não valer nem para uma combinação, então não é um triângulo verdadeiro. Como as seguintes afirmações são verdadeiras, você encontrou um triângulo válido:

6. Saiba como descobrir um triângulo inválido. Só para pegar o jeito, mas você precisa ter certeza de que consegue identificar um triângulo que não está certo. Suponha que você esteja lidando com os seguintes três lados e os comprimentos: 5, 8 e 3. Vamos ver se eles passam no teste:
Pontas
- Isso sempre se aplica, desde que você não cometa nenhum erro de cálculo, e se for uma adição regular, é muito simples.
Artigos sobre o tópico "Determine se três comprimentos juntos formam um triângulo"
Оцените, пожалуйста статью
Popular