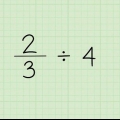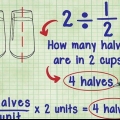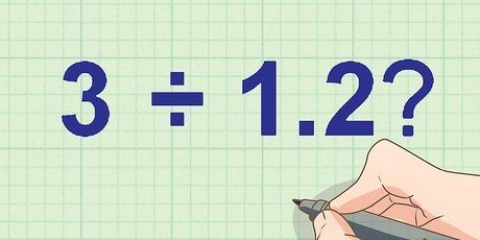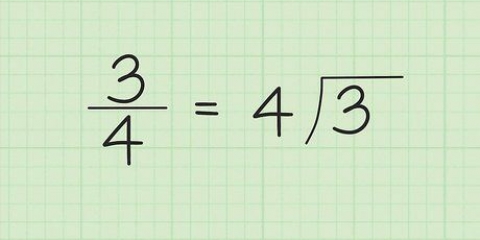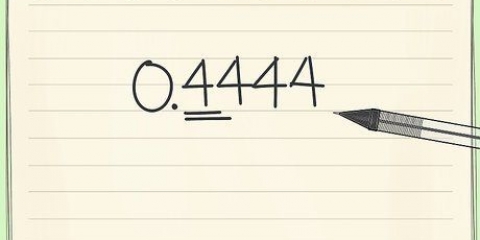Dividindo um inteiro por uma fração

Contente

Se você quiser dividir um número inteiro por uma fração, você realmente calcula quantos `grupos` da fração vão para o todo. A maneira padrão de dividir um número inteiro por uma fração é multiplicar o número inteiro pelo inverso da fração. Você também pode criar um gráfico para ajudar a visualizar esse cálculo.

Degraus

Método 1 de 3: Multiplique pelo inverso

Imagem intitulada Divida um número inteiro com uma fração Etapa 1
1. Converter o número inteiro em uma fração. Você faz isso transformando o número inteiro no numerador de uma fração. Faça o denominador 1.
  • Por exemplo: Calcule seu 7÷34{displaystyle 7div {frac {3}{4}}}{displaystyle 7div {frac {3}{4}}}, então você muda primeiro 7{estilo de exibição 7}7 dentro 71{displaystyle {frac {7}{1}}}{displaystyle {frac {7}{1}}}.
Imagem intitulada Divida um número inteiro com uma fração Etapa 2
2. Encontre o inverso da fração. O inverso de um número é igual ao inverso desse número. Para encontrar o inverso de uma fração, troque o numerador e o denominador.
  • Por exemplo: o inverso (o inverso) de 34{displaystyle {frac {3}{4}}}{frac{3}{4}} é 43{displaystyle {frac {4}{3}}}{displaystyle {frac {4}{3}}}.
    • Imagem intitulada Divida um número inteiro com uma fração Etapa 3
    3. Multiplique as duas frações. Para multiplicar frações, primeiro multiplique os numeradores. Depois multiplique os denominadores. O produto das duas frações é igual ao quociente do seu problema de divisão original.
  • Por exemplo: 71×43=283{displaystyle {frac {7}{1}}times {frac {4}{3}}={frac {28}{3}}}{displaystyle {frac {7}{1}}times {frac {4}{3}}={frac {28}{3}}}
    • Imagem intitulada Dividir um número inteiro por uma fração Etapa 4
    4. Simplifique, se necessário. Se você tiver uma fração imprópria (ou seja, o numerador é maior que o denominador), o problema pode solicitar que você a altere para um número misto. Normalmente, a declaração pedirá para simplificar frações para os termos mais baixos.
  • Por exemplo: 283{displaystyle {frac {28}{3}}}{displaystyle {frac {28}{3}}} pode ser simplificado para o número misto 913{displaystyle 9{frac {1}{3}}}{displaystyle 9{frac {1}{3}}}.

    • Método 2 de 3: desenhando um diagrama

    Imagem intitulada Divida um número inteiro com uma fração Etapa 5
    1. Desenhe formas que representem o número inteiro. Sua forma deve poder ser dividida em grupos iguais, como um quadrado ou um círculo. Desenhe as formas tão grandes que você possa dividi-las em pedaços menores.
    • Por exemplo: no cálculo 5÷34{displaystyle 5div {frac {3}{4}}}{displaystyle 5div {frac {3}{4}}}, você desenharia cinco círculos.
    Imagem intitulada Divida um número inteiro com uma fração Etapa 6
    2. Divida cada forma inteira pelo denominador da fração. O denominador de uma fração informa em quantas partes uma forma inteira é dividida. Divida cada forma inteira em suas partes, conforme indicado pela fração.
  • Por exemplo, se você dividir por 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, então o 4 no denominador indica que você tem que dividir o todo em quatro partes iguais.
    • Imagem intitulada Dividir um número inteiro com uma fração Etapa 7
    3. Sombreie os grupos que representam a fração. Como você divide o número inteiro pela fração, você vê quantos grupos da fração estão no número inteiro. Então primeiro você indica os grupos. Pode ser útil dar a cada grupo uma cor diferente, pois alguns grupos têm partes em duas formas inteiras diferentes. Deixe as peças restantes em branco.
  • Por exemplo: imagine a parte 5 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, então você colore três quartos em uma cor diferente para cada grupo. Observe que muitos grupos conterão dois quartos em um todo e um quarto em outro inteiro.
    • Imagem intitulada Dividir um número inteiro com uma fração Etapa 8
    4. Contar o número de grupos inteiros. Isso lhe dará o número inteiro de sua resposta.
  • Por exemplo, você tinha seis grupos de 34{displaystyle {frac {3}{4}}}{frac{3}{4}} tem que fazer os cinco círculos.
    • Imagem intitulada Dividir um número inteiro com uma fração Etapa 9
    5. Interprete as peças restantes. Compare o número de peças que você deixou com um grupo inteiro. A fração de um grupo que você deixou indica a fração de sua resposta. Tenha cuidado para não comparar o número de peças que você tem com o número de peças que você tem com uma forma inteira, pois isso lhe dará a fração errada.
  • Por exemplo: depois de dividir as cinco formas em grupos de 34{displaystyle {frac {3}{4}}}{frac{3}{4}}, você tem dois quartos, ou 24{displaystyle {frac {2}{4}}}{displaystyle {frac {2}{4}}} cerca de. Como um grupo inteiro é composto de três peças e você tem duas peças, sua fração é 23{displaystyle {frac {2}{3}}}{frac{2}{3}}.
    • Imagem intitulada Divida um número inteiro com uma fração Etapa 10
    6. Anote a resposta. Combine os grupos do número inteiro com os grupos da fração para encontrar o quociente da soma da divisão original.
  • Por exemplo: 5÷34=623{displaystyle 5div {frac {3}{4}}=6{frac {2}{3}}}{displaystyle 5div {frac {3}{4}}=6{frac {2}{3}}}.

    • Método 3 de 3: Exemplos de Problemas com Soluções

    Imagem intitulada Dividir um número inteiro com uma fração Etapa 11
    1. Resolver: Com que frequência 12{displaystyle {frac {1}{2}}}{frac{1}{2}} dentro 8{estilo de exibição 8}{estilo de exibição 8}?
    • Como a tarefa pergunta quantos grupos de 12{displaystyle {frac {1}{2}}}{frac{1}{2}} indo em 8 é uma soma de divisão.
    • Faça uma fração de 8, tornando-a um numerador com denominador 1: 8=81{displaystyle 8={frac {8}{1}}}{displaystyle 8={frac {8}{1}}}.
    • Encontre o inverso da fração invertendo o numerador e o denominador: 12{displaystyle {frac {1}{2}}}{frac{1}{2}} torna-se 21{displaystyle {frac {2}{1}}}{displaystyle {frac {2}{1}}}.
    • Multiplique as duas frações: 81×21=161{displaystyle {frac {8}{1}}times {frac {2}{1}}={frac {16}{1}}}{displaystyle {frac {8}{1}}times {frac {2}{1}}={frac {16}{1}}}.
    • Simplifique, se necessário: 161=16{displaystyle {frac {16}{1}}=16}{displaystyle {frac {16}{1}}=16}.
    Imagem intitulada Dividir um número inteiro com uma fração Etapa 12
    2. Resolver:16÷58{displaystyle 16div {frac {5}{8}}}{displaystyle 16div {frac {5}{8}}}.
  • Faça uma fração de 16, tornando-a um numerador com o denominador 1: 16=161{displaystyle 16={frac {16}{1}}}{displaystyle 16={frac {16}{1}}}.
  • Encontre o inverso da fração invertendo o numerador e o denominador: 58{displaystyle {frac {5}{8}}}{displaystyle {frac {5}{8}}} torna-se 85{displaystyle {frac {8}{5}}}{displaystyle {frac {8}{5}}}.
  • Multiplique as duas frações: 161×85=1285{displaystyle {frac {16}{1}}times {frac {8}{5}}={frac {128}{5}}}{displaystyle {frac {16}{1}}times {frac {8}{5}}={frac {128}{5}}}.
  • Simplifique, se necessário: 1285=2535{displaystyle {frac {128}{5}}=25{frac {3}{5}}}{displaystyle {frac {128}{5}}=25{frac {3}{5}}}.
    • Imagem intitulada Dividir um número inteiro com uma fração Etapa 13
    3. Resolva o seguinte problema desenhando um diagrama. Rufus tem nove latas de feijão. Ela come todos os dias 23{displaystyle {frac {2}{3}}}{frac{2}{3}} uma lata. Por quantos dias ela tem latas?
  • Desenhe nove círculos para representar as nove latas.
  • Porque ela 23{displaystyle {frac {2}{3}}}{frac{2}{3}} coma de cada vez, divida cada círculo em terços.
  • Pinte os grupos de 23{displaystyle {frac {2}{3}}}{frac{2}{3}}.
  • Contar o número de grupos completos. Deve ser 13.
  • Interprete as peças restantes. Falta uma peça, e essa é 13{displaystyle {frac {1}{3}}}{frac{1}{3}}. Porque todo um grupo 23{displaystyle {frac {2}{3}}}{frac{2}{3}} é, você tem metade de um grupo restante. Então a fração é 12{displaystyle {frac {1}{2}}}{frac{1}{2}}.
  • Combine o número de grupos de inteiros e frações para encontrar sua resposta final: 9÷23=1312{displaystyle 9div {frac {2}{3}}=13{frac {1}{2}}}{displaystyle 9div {frac {2}{3}}=13{frac {1}{2}}}.

    • Pr.FaqCartx.info / Educação e comunicação
    Оцените, пожалуйста статью
    Novo
    Adicione fotos à sua galeria em um iphone
    Adicione fotos à sua galeria em um iphone
    Ocultar álcool
    Ocultar álcool
    Aplique base e pó
    Aplique base e pó
    Dançando a valsa
    Dançando a valsa
    Melhore a recepção wi-fi
    Melhore a recepção wi-fi
    Faça suas próprias roupas
    Faça suas próprias roupas