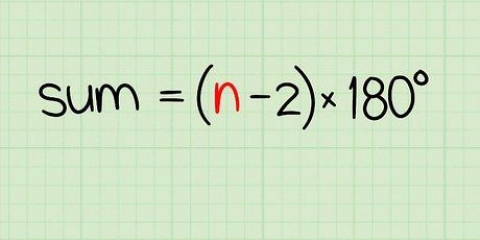Os ângulos em um triângulo (um polígono de 3 lados) totalizam 180 graus. Os ângulos em um quadrilátero (um polígono de 4 lados) totalizam 360 graus. Os ângulos em um pentágono (um polígono de 5 lados) totalizam 540 graus. Os ângulos em um hexágono (um polígono de 6 lados) totalizam 720 graus. Os ângulos em um octógono (um polígono de 8 lados) totalizam 1080 graus. 
Se o polígono for um polígono regular, basta dividir o total de todos os ângulos pelo número de ângulos. Assim, qualquer ângulo em um triângulo equilátero é 180/3 = 60 graus, e qualquer ângulo de um quadrado é 360/4 = 90 graus. (Embora, por definição, um retângulo não seja um polígono regular, todos os ângulos também são ângulos retos e, portanto, 90 graus). Se um polígono não for um polígono regular, você precisará saber a magnitude dos outros ângulos para calcular a magnitude do ângulo desconhecido. vá para o próximo passo. 
Se dois dos ângulos de um triângulo são 60 e 80 graus, some esses ângulos (60 + 80 = 140). Em seguida, subtraia esta soma do total dos ângulos de um triângulo, 180 graus: 180-140 = 40 graus. (Tal triângulo, onde todos os ângulos são diferentes, é chamado de triângulo escaleno). Você pode escrever o método acima como uma fórmula: uma=180 – (b + c), através do qual uma é o ângulo que você deseja determinar, e b e c os ângulos conhecidos. Para polígonos com mais de 3 lados, substitua `180` pelo total dos ângulos específicos daquele polígono e adicione um termo diferente para cada ângulo conhecido adicional. Para alguns polígonos é possível uma `solução mais rápida` para determinar o ângulo desconhecido. Um triângulo isósceles é um triângulo com dois lados de igual comprimento e dois ângulos de mesma magnitude. Um paralelogramo é um quadrilátero com lados opostos de igual comprimento e ângulos diagonalmente opostos de mesma magnitude. 

Se você conhece o comprimento do lado oposto (em relação ao ângulo) e o comprimento da hipotenusa (o lado oposto ao ângulo reto), use a função seno (o comprimento do lado oposto dividido pelo comprimento da hipotenusa). seda). Se você conhece o comprimento do lado retangular adjacente e o comprimento da hipotenusa, você pode usar a função cosseno (o comprimento do lado adjacente dividido pelo comprimento da hipotenusa). Se você conhece os comprimentos dos lados opostos e adjacentes, pode usar a função tangente (o comprimento do lado oposto dividido pelo comprimento do lado adjacente). 
Dividindo o valor oposto 5 pela hipotenusa (a hipotenusa) 10 dá a fração 5/10=0,5. 
Nos dias anteriores às calculadoras, você deve consultar uma tabela impressa de valores para seno, cosseno e tangente de ângulos de 0 a 90 graus. Siga a coluna do seno até encontrar o valor `0,5` e, em seguida, encontre o ângulo que corresponde a esse valor do seno. Se você tiver uma calculadora com funções trigonométricas, poderá inserir o seno como valor (se ainda não tiver usado a calculadora para dividir o oposto pela hipotenusa para encontrar esse valor) e pressionar a tecla ou teclas apropriadas. Dependendo da marca da calculadora, pressione uma única tecla rotulada `sin` ou uma tecla rotulada `Inv`, `2ndF` ou `Shift` antes de pressionar a tecla `sin`. Qualquer que seja o método usado para resolver este exemplo, em todos os casos você deve encontrar um ângulo de 30 graus.
Calcular ângulos
Contente
Em geometria, um ângulo é o espaço entre dois raios ou segmentos de linha que têm o mesmo ponto final ou vértice. A maneira mais comum de medir ângulos é em graus, onde um círculo completo é de 360 graus. Você pode calcular o ângulo em um polígono se souber a forma do polígono e o tamanho dos outros ângulos ou, no caso de um triângulo retângulo, se souber o tamanho dos dois lados.
Degraus
Método 1 de 2: Calculando o ângulo em um polígono

1. Contar o número de lados do polígono.

2. Encontre a soma de todos os ângulos no polígono. A fórmula para encontrar a medida total de todos os ângulos internos de um polígono é (n – 2) x 180, onde n é o número de lados, bem como o número de ângulos do polígono. Alguns totais comuns dos ângulos em um polígono são:

3. Determine se o polígono é um polígono regular. Um polígono regular é um polígono com todos os lados do mesmo comprimento e todos os ângulos do mesmo tamanho. Triângulos e quadrados equiláteros são exemplos de polígonos regulares, enquanto o Pentágono em Washington DC é um exemplo de pentágono regular e um sinal de pare é um exemplo de octógono regular.

4. Some os ângulos conhecidos do polígono e subtraia o total do total de todas as medidas de ângulo do polígono. A maioria dos problemas de geometria semelhantes funciona com triângulos ou quadriláteros porque há menos números para processar e, portanto,.
Método 2 de 2: Calcular o ângulo em um triângulo retângulo

1. Descubra o que você já sabe. Um triângulo retângulo é assim chamado porque um de seus ângulos é um ângulo reto. Você pode determinar os outros ângulos se souber algum dos seguintes:
- O tamanho do terceiro ângulo. Nesse caso, você pode adicionar o tamanho do ângulo a 90, o número de graus do ângulo reto e subtrair o total de 180.
- O tamanho dos dois lados do triângulo. Neste caso, você pode determinar a magnitude do ângulo usando trigonometria.

2. Determine qual função trigonométrica usar. Funções trigonométricas são razões entre dois dos três lados de um triângulo. Embora existam seis funções trigonométricas, as três seguintes são mais comumente usadas:

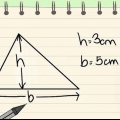
3. Encontre a razão entre os dois lados conhecidos. Para os propósitos deste exemplo, suponha que o lado oposto ao ângulo tenha um comprimento de 5 e a hipotenusa tenha um comprimento de 10. Uma vez que o oposto e a hipotenusa são dados, a razão com a qual estamos lidando aqui é a do seno.

4. Encontre o ângulo correspondente à razão da função trigonométrica. Como estamos usando o seno para encontrar o ângulo, o ângulo que estamos procurando é chamado de arco seno ou seno inverso. Existem duas maneiras de encontrá-lo:
Pontas
- Os ângulos são referidos pelo número de graus que medem. Como mencionado acima, um ângulo reto tem 90 graus. Um ângulo maior que 0, mas menor que 90 graus é um ângulo agudo. Um ângulo maior que 90, mas menor que 180 graus é um ângulo obtuso. Um ângulo de 180 graus é um ângulo reto, enquanto um ângulo maior que 180 graus é um ângulo de reentrada.
- Dois ângulos com um total de 90 graus são chamados de ângulos complementares (Os dois ângulos diferentes do ângulo reto em um triângulo retângulo são ângulos complementares). Dois ângulos cujos ângulos somam 180 graus são chamados de ângulos suplementares.
Necessidades
- Tabelas trigonométricas ou uma calculadora com funções trigonométricas
Artigos sobre o tópico "Calcular ângulos"
Оцените, пожалуйста статью
Popular