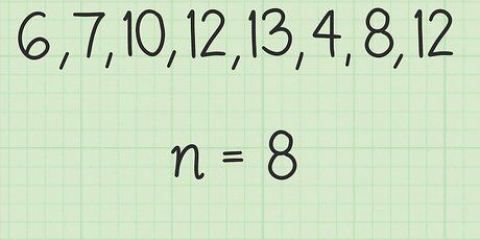Como regra geral, o nível de significância (ou alfa) geralmente é definido como 0,05, o que significa que a probabilidade de observar acidentalmente as diferenças presentes em seus dados é de apenas 5%. Um nível de confiança mais alto (e, portanto, um valor p mais baixo) significa que os resultados são mais significativos. Se você quiser que os dados sejam mais confiáveis, defina o valor p abaixo de 0,01. Valores p mais baixos são comumente usados na indústria ao depurar produtos. É muito importante poder ter grande confiança de que cada peça está funcionando exatamente como deveria. Para a maioria dos experimentos em direção a uma hipótese, um nível de significância de 0,05 é aceitável. 
Se você não tiver certeza se seus dados estão acima ou abaixo do grupo de controle, use um teste duplo. Permite testar a significância em ambas as direções. Se você sabe em qual direção seus dados tendem a se mover, use um teste unilateral. No exemplo dado, você espera que as notas dos alunos melhorem; é por isso que você usa um teste unilateral. 
Os pesquisadores geralmente fazem um pequeno estudo piloto para informar sua análise de força e determinar o tamanho da amostra necessário para um estudo maior e mais abrangente. Se você não tiver recursos para fazer um estudo piloto complexo, faça algumas estimativas de possíveis médias com base na leitura da literatura e nos estudos que outros indivíduos possam ter feito. Isso lhe dará um bom ponto de partida para o tamanho da amostra para começar. 

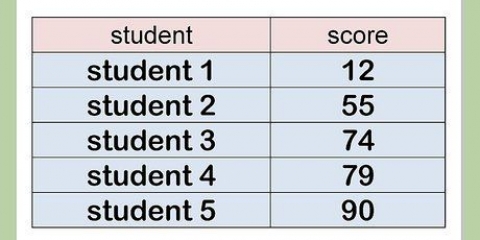
Por exemplo, para encontrar a nota média do grupo que leu o material antes da aula, vejamos alguns dados. Para simplificar, usamos um conjunto de dados de 5 pontos: 90, 91, 85, 83 e 94. Some todos os dados: 90 + 91 + 85 + 83 + 94 = 443. Divida a soma pelo número de dados, N = 5:443 / 5 = 88,6. A nota média deste grupo é 88,6. 
(90-88,6), (91-88,6), (85-88,6), (83-88,6) e (94-88,6). Os números calculados agora são 1,4, 2,4, -3,6, -5,6 e 5,4. 
Em nosso exemplo, agora estamos trabalhando com 1,96 5,76, 12,96, 31,36 e 29,16. Somando esses quadrados dá: 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2. 
Subtrair: N – 1 = 5 – 1 = 4 Parte: 81,2/4 = 20,3 
Em nosso exemplo, o desvio padrão das notas finais dos alunos que leram o material antes da aula é: s = √20,3 = 4,51. 

µ1 é a média do primeiro grupo. µ2 é a média do segundo grupo. sd é a variação entre as amostras. Use a média maior como µ1, então você não tem um valor negativo para t. Em nosso exemplo, digamos que a média amostral para o Grupo 2 (aqueles que não leram) foi 80. O t-score é então: t = (µ1 – µ2)/sd = (88,6 – 80)/3,29 = 2,61. 

com 8 dias.f. e um t-score de 2,61, o valor p para um teste unilateral fica entre 0,01 e 0,025. Como nosso nível de significância definido é menor ou igual a 0,05, nossos dados são estatisticamente significativos. Com esses dados, rejeitamos a hipótese nula e aceitamos a hipótese alternativa: Alunos que lêem o material antes da aula obtêm melhores notas finais. 
Avaliar a significância estatística
Contente
O teste de hipóteses é apoiado por análise estatística. A significância estatística é calculada a partir de um valor p, que indica a probabilidade do resultado observado, dado que um determinado teorema (a hipótese nula) é satisfeito. Se este valor p for menor que o nível de significância declarado (geralmente 0,05), então o experimentador pode assumir que a hipótese nula é falsa e aceitar a hipótese alternativa. Usando um teste t simples, você pode calcular um valor p e comparar a significância entre dois grupos diferentes de um conjunto de dados.
Degraus
Parte 1 de 3: Configurando seu experimento

1. Defina sua hipótese. O primeiro passo para avaliar a significância estatística é definir a pergunta a ser respondida e colocar sua hipótese. A hipótese é uma afirmação sobre seus dados experimentais e as diferenças que podem existir na população. Em todo experimento existe uma hipótese nula e uma hipótese alternativa. Em geral, você comparará dois grupos para ver se eles são iguais ou diferentes.
- A hipótese nula (H0) geralmente afirma que não há diferença entre seus dois conjuntos de dados. Por exemplo: alunos que leram o material antes da aula não obtêm melhores notas finais.
- A hipótese alternativa (Huma) é o oposto da hipótese nula e é a afirmação que você está tentando apoiar com seus dados experimentais. Por exemplo: alunos que leram o material antes da aula obtêm melhores notas finais.

2. Defina o nível de significância para determinar o quão incomum seus dados devem ser antes de serem considerados significativos. O nível de significância (também chamado alfa) é o limite que você define para determinar a significância. Se o valor p for menor ou igual ao nível de significância definido, os dados podem ser considerados estatisticamente significativos.

3. Decidir usar um teste unicaudal ou bicaudal. Uma das suposições que um teste t faz é que os dados são normalmente distribuídos. Uma distribuição normal de dados forma uma curva de sino com a maioria dos dados de teste caindo no meio. O teste t é um teste matemático para ver se os dados estão fora da distribuição normal (acima ou abaixo), nas `caudas` da curva.

4. Determine o tamanho da amostra com uma análise de força. O poder de um teste é a probabilidade de que o resultado esperado seja observado, dado um tamanho de amostra específico. O limiar comum para força (ou β) é 80%. Uma análise de poder pode ficar um pouco complicada sem alguns dados preliminares porque você precisa de algumas informações sobre os valores médios esperados entre cada grupo e seus desvios padrão. Use uma calculadora de análise de força online para determinar o tamanho de amostra ideal para seus dados.
Parte 2 de 3: Calculando o desvio padrão

1. Encontre a fórmula para o desvio padrão. O desvio padrão é uma medida da dispersão dos seus dados. Ele fornece informações sobre a semelhança de cada ponto de dados em sua amostra. À primeira vista, a equação pode parecer um pouco complicada, mas as etapas a seguir o guiarão pelo cálculo. A fórmula é: s = √∑((xeu – µ)/(N – 1)).
- s é o desvio padrão.
- ∑ indica que você precisa somar todos os valores de amostra coletados.
- Xeu representa cada valor individual de seus dados.
- µ é a média (ou centro) de seus dados para cada grupo.
- N é o total da amostra.

2. Média dos dados de teste em cada grupo. Para calcular o desvio padrão, você deve primeiro calcular a média dos dados de teste nos grupos individuais. A média é denotada pela letra grega mu ou µ. Para fazer isso, some cada parte dos dados e divida-os pelo número total de dados.

3. Subtraia cada métrica da média. A próxima parte do cálculo inclui a parte (xeu – µ) da equação. Você subtrai cada dado da média calculada. Em nosso exemplo, você acaba com cinco subtrações.

4. Eleve ao quadrado cada um desses números e some-os. Cada um dos novos números que você acabou de calcular agora será elevado ao quadrado. Esta etapa também cria sinais negativos. Se você tiver um sinal de menos após esta etapa ou no final do cálculo, pode ter esquecido esta etapa.

5. Divida isso pelo tamanho da amostra total, menos 1. A fórmula divide por N-1, porque corrige o fato de você ainda não ter contado uma população inteira; você pega uma amostra da população de todos os alunos para fazer uma estimativa.

6. Tire a raiz quadrada. Depois de dividir pelo número de dados menos um, calcule a raiz quadrada desse último número. Este é o último passo no cálculo do desvio padrão. Existem programas estatísticos que podem fazer esse cálculo para você, após inserir os dados brutos.
Parte 3 de 3: Determine o significado

1. Calcule a diferença entre seus dois grupos da amostra. Até este ponto, o exemplo cobriu apenas um dos grupos de amostra. Se você quiser comparar dois grupos, é claro que terá dados de ambos os grupos. Calcule o desvio padrão do segundo grupo de dados de teste e use-o para calcular a diferença entre os dois grupos experimentais. A fórmula da variância é sd = √((s1/N1) + (s2/N2)).
- sd é a variação entre seus grupos.
- s1 é o desvio padrão do grupo 1, e N1 é o tamanho da amostra do grupo 1.
- s2 é o desvio padrão do grupo 2, e N2 é o tamanho da amostra do grupo 2.
- Para o nosso exemplo, digamos que os dados do Grupo 2 (alunos que não leram antes da aula) tenham um tamanho de amostra de 5 e um desvio padrão de 5,81. A variação é:
- sd = √((s1)/N1) + ((s2)/N2))
- sd = √(((4,51)/5) + ((5,81)/5)) = √((20,34/5) + (33,76/5)) = √(4,07 + 6,75) = √10,82 = 3,29.

2. Calcule o t-score dos seus dados. Com um t-score, você pode converter dados em um formulário que pode ser comparado com outros dados. Com pontuações t, você pode realizar um teste t, para calcular a probabilidade de dois grupos diferirem significativamente um do outro. A fórmula para um t-score é: t = (µ1 – µ2)/sd.

3. Determine o grau de liberdade da sua amostra. Ao usar o t-score, os graus de liberdade são determinados usando o tamanho da amostra. Some o número de dados de teste de cada grupo e divida por dois. Em nosso exemplo, os graus de liberdade; d.f.) 8, pois havia cinco dados no primeiro grupo e cinco no segundo grupo ((5 + 5) – 2 = 8).

4. Use uma tabela t para avaliar a significância. Uma tabela com pontuações t e o número de graus de liberdade pode ser encontrada em um livro de estatística padrão ou online. Olhe para a linha de graus de liberdade para seus dados e encontre o valor p que corresponde ao seu t-score.

5. Considere um estudo de acompanhamento. Muitos pesquisadores fazem um pequeno estudo piloto com algumas medidas para entender como montar um estudo maior. Outro estudo, com mais medições, ajudará a aumentar sua confiança em sua conclusão.
Pontas
- A estatística é um campo extenso e complicado. Faça uma aula de ensino médio ou superior sobre inferência estatística para entender melhor a significância estatística.
Avisos
- Esta análise é específica para um teste t para testar as diferenças entre duas populações normalmente distribuídas. Você pode precisar de um teste estatístico diferente, dependendo da complexidade de sua coleta de dados.
Artigos sobre o tópico "Avaliar a significância estatística"
Оцените, пожалуйста статью
Popular